某类上半平面的调和拟共形同胚的凸组合

孙祚晨，王麒翰，龙波涌

（安徽大学数学科学学院，安徽合肥230601）

拟共形映射的边界对应问题是拟共形映射理论中十分重要的内容，它包括拟共形映照边界函数和给定边界函数的拟共形延拓问题，这些都有利于拟共形映照理论中极值问题的研究。设f(z)为区域D上的保向微分同胚，如果存在常数1≤K＜∞，使 得 伸 张 函 数 满 足 D(z)=,则称f(z)为区域D上的K-拟共形映射[1]。若进一步假设f(z)在区域D上有二阶连续偏导数，且满足=0，则称 f(z)为区域D上的调和拟共形映射。关于平面上的调和映射，可参见文献[2-3]。

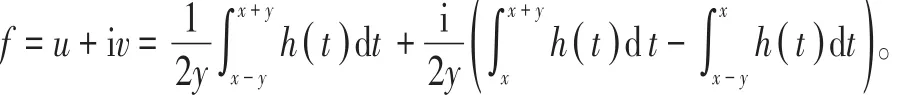
记HQS( R )为上半平面到其自身的调和拟共形同胚定义在实轴上的值。Kalaj和Pavlovic[3]于2005年证明了以下定理：

定理1[3]设h(x)为R上的单调增加同胚，则h(x ) ∈HQS( R )当且仅当h(x)满足双Lipschitz条件且H(h′)∈ L∞(R)。

上面的H(h′)表示h(x)的Hilbert变换，定义为

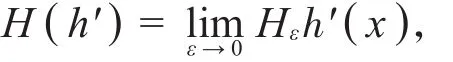
其中

定理2[4]上半平面到其自身的调和拟共形同胚具有如下形式：

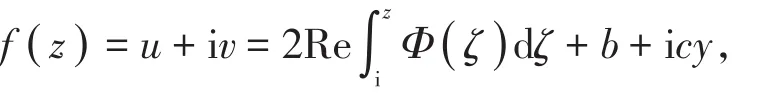
其中，b+ic∈H，Φ(z)为H上的解析函数且Φ( H )为右半平面的相对紧集。

关于Beurling-Ahlfors延拓的伸张函数估计问题，一直以来都得到了极大的关注并被深入地研究[1,5-6]。至今为止，伸张函数D(z)的最好估计是D ＜ min{2ρ-1,ρ32}[6]。

继文献[3]后，文献[7]对边界函数做了进一步研究，得到将边界函数延拓成上半平面到自身的调和拟共形同胚的简单判别条件。文献[8]判断了边界函数h(x)=x+sinπx，0≤k＜1可以延拓成上半平面到自身的调和拟共形同胚，给出了具体表达式并对其伸张函数D(z)做了估计。对于单叶的边界函数，Macgregor指出两个单叶解析函数的凸组合不一定还是单叶函数[9]。对于一类可延拓成上半平面到其自身的调和拟共形同胚的边界函数，本文证明了其凸组合依然可以延拓成上半平面到其自身的调和拟共形同胚。给出了具体的表达式，估计了其伸张函数。

通过以上研究，得到了以下结论：

定理3设

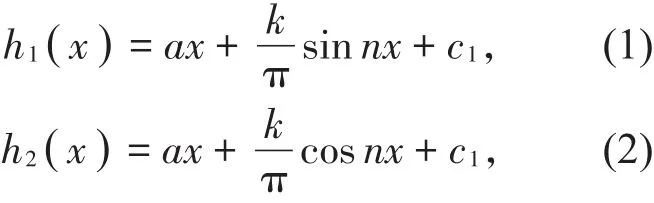
其中n∈N*，0≤k＜a，则其可以延拓成上半平面到其自身的调和拟共形同胚，其对应的表达式分别为

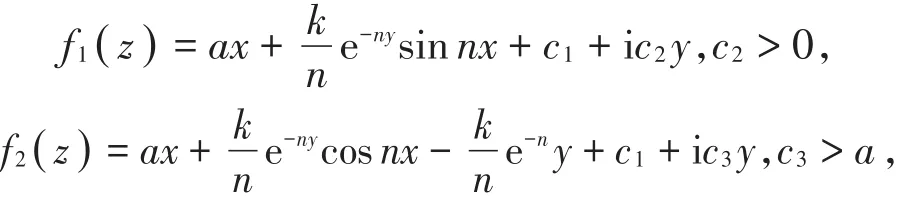
其伸张函数估计式分别为

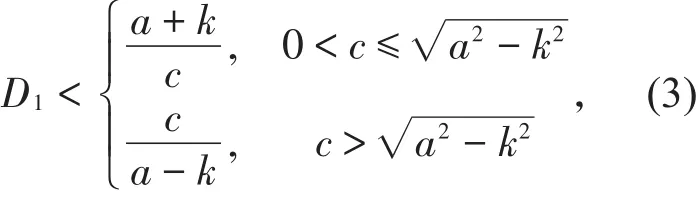
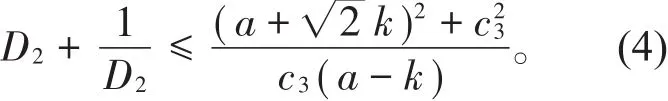
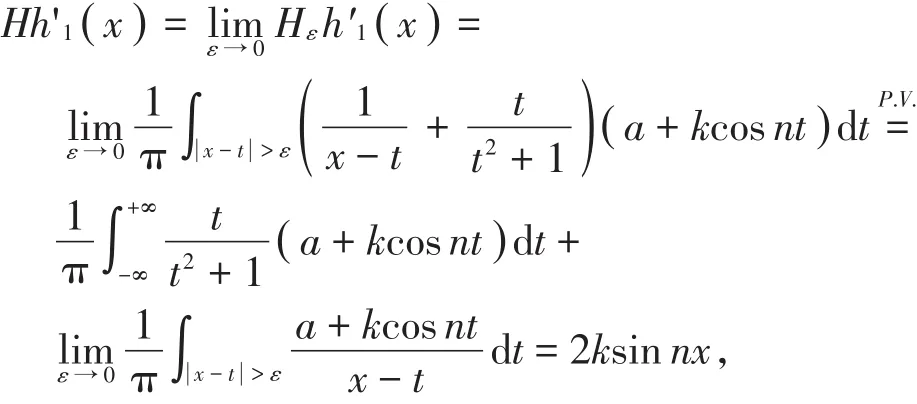
则Hh1′(x)∈ L∞(R)。又由定理1知，h1(x)可以延拓为上半平面到自身的调和拟共形映射。令

经过计算可得

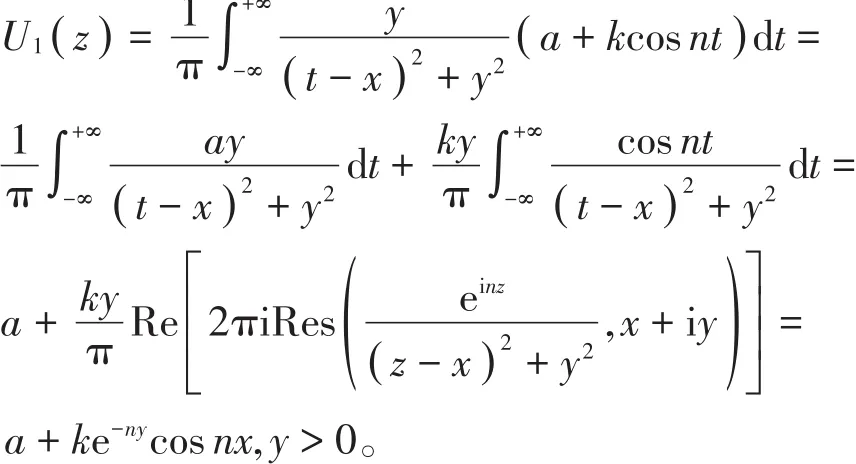
设V1是 U1满足V1(i)=0共轭调和，则V1(z)=ke-nysinnx，解析函数为

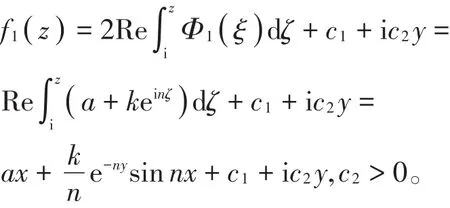
再估计f1(z)的最大伸张函数，令

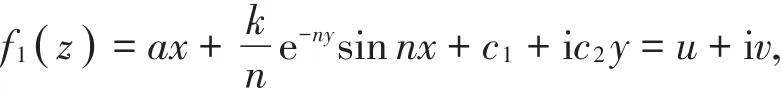
则ux=a+ke-nycosnx,uy=-ke-nysinnx,vx=0,vy=c2。

其中

计算得

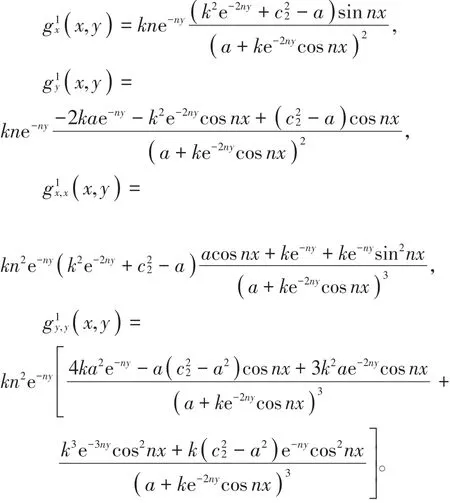
因此得到，

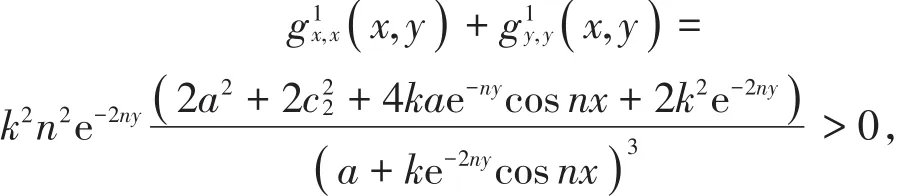
则g1(x,y)为次调和的，即D1+在上半平面是次调和，所以D+的最大值只能在边界取得。

令

下面求S(x)的最大值。

(1)当0＜c2＜时，

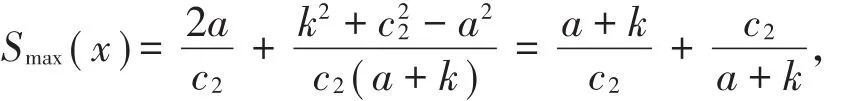
其中

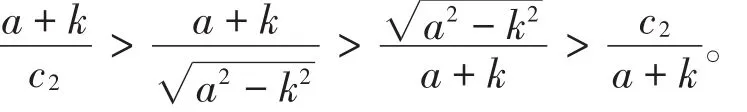
(2)当c2＞时，

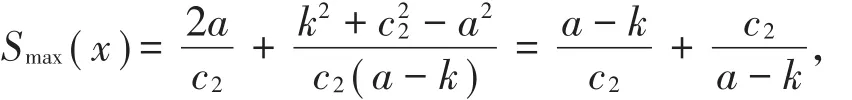
其中

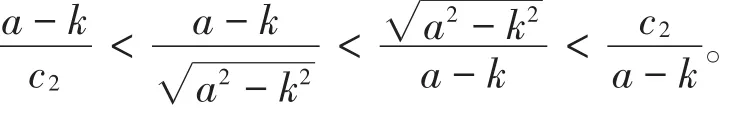
(3)当c2=时，

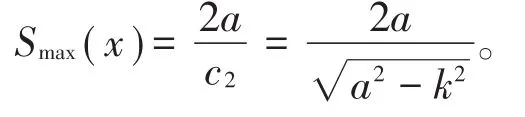
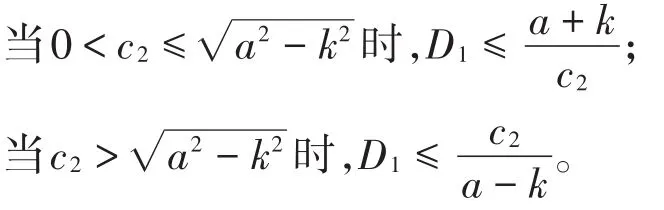
h2(x)的情况类似可得。容易验证Hh'2(x)∈L∞(R)且h2(x)是双利普希茨的。计算可得U2(z ) =a-ke-nysinnx,V2(z ) =ke-nycosnx+，则其上半平面到自身的调和拟共形延拓表达式为

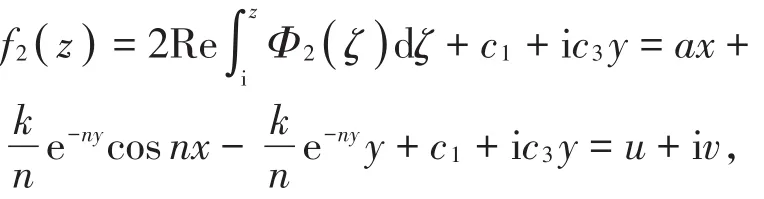
则

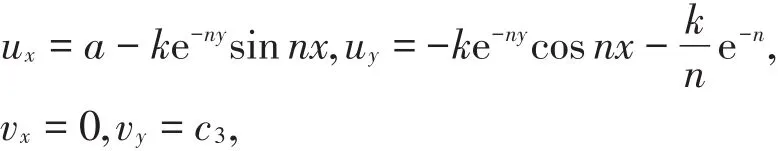
则

其中

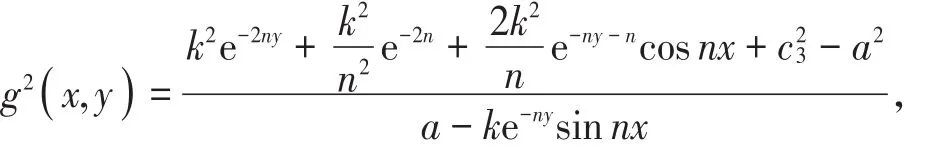
计算得

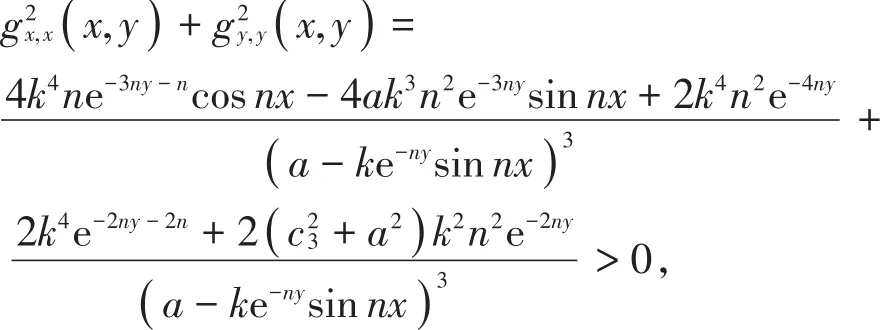
可得g2(x,y)为次调和的，即D2+在上半平面是次调和，故最大值只能在边界取得，则

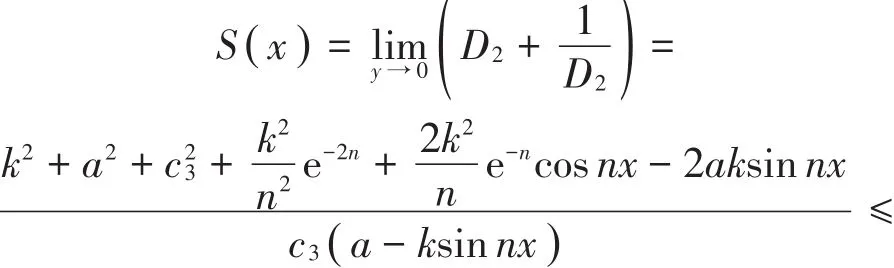
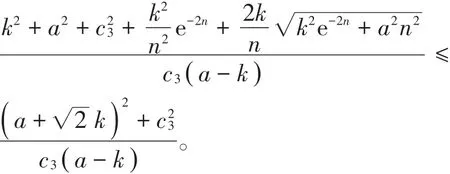
定理4 设h3(x)=bh1+(1-b)h2,n∈N*,0≤ k＜ a，其中h1和h2分别由定理3中的(1)和(2)式定义，则其上半平面到自身的调和拟共形延拓表达式为

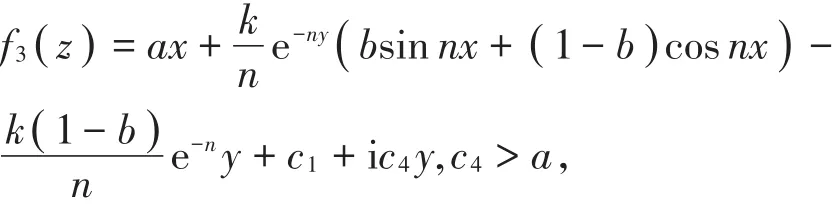
其伸张函数有估计式

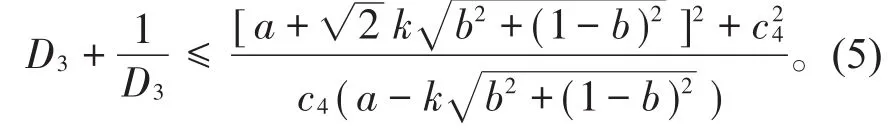
证明 由定理3很容易证明h3()x是双利普希茨的，且

则Hh′3(x)∈ L∞(R)，即h3(x)可调和拟共形延拓到上半平面。易得

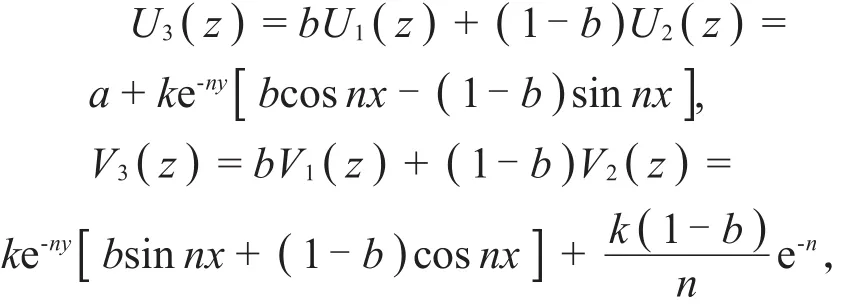
解析函数

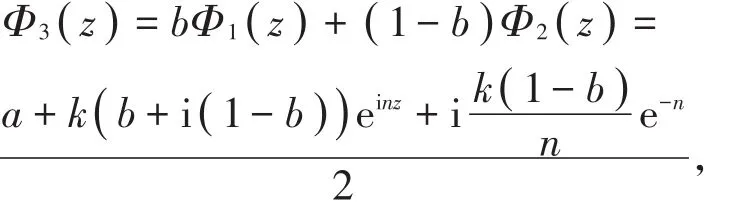
则其上半平面的调和拟共形延拓表达式为

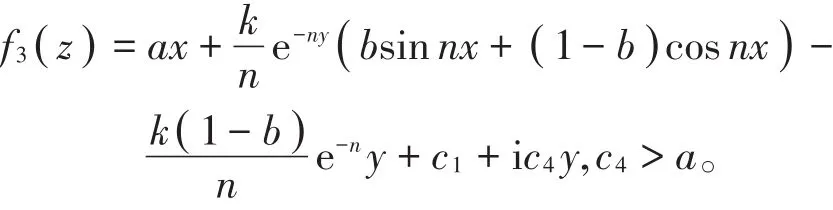
再估计f3(z)的最大伸张函数，令f3(z)=u+iv，则

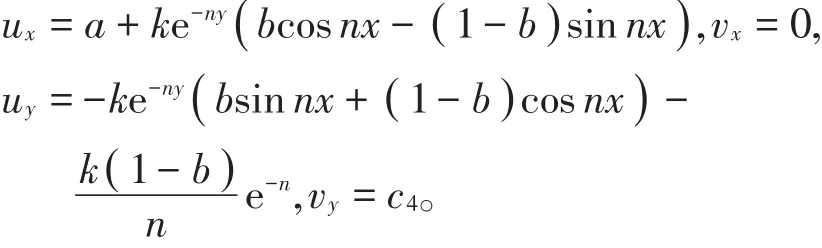
计算可得

其中

直接计算得

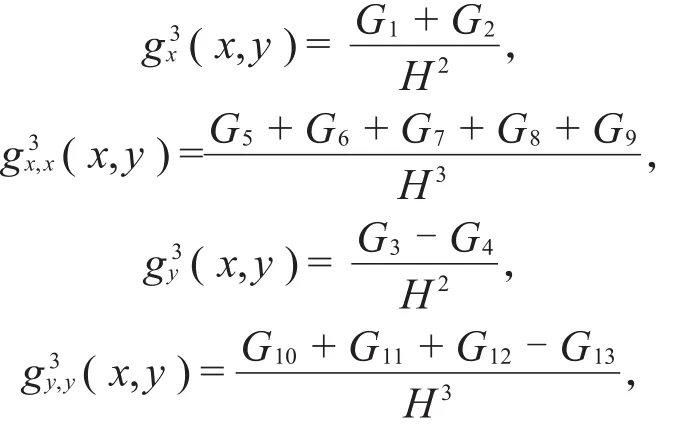
则得到

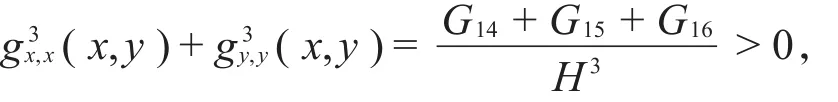
其中

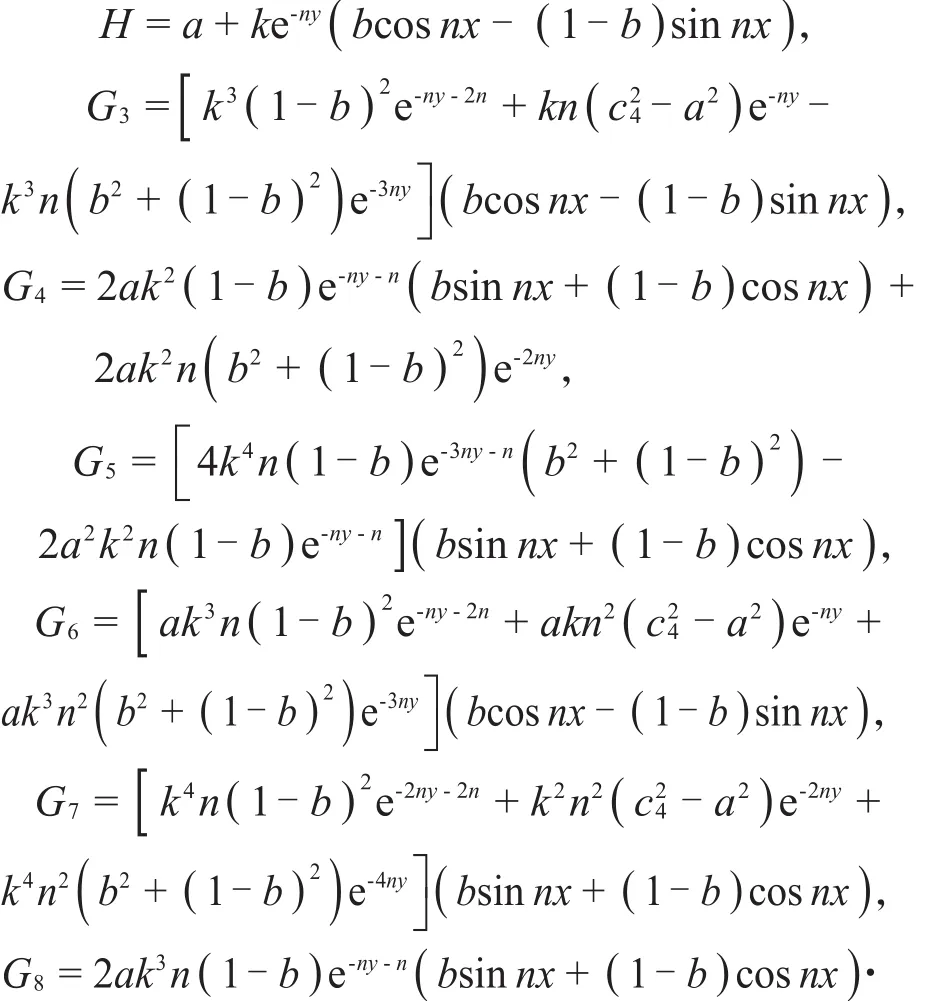
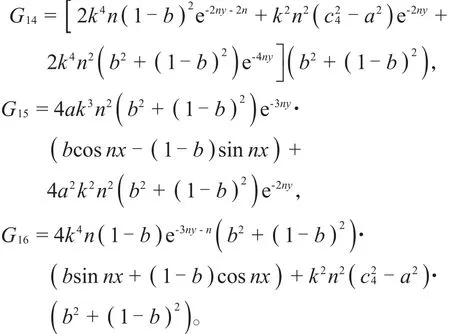
可得g3(x ,y)为次调和的，即D3+在上半平面是次调和，那么最大值只能在边界取得。令

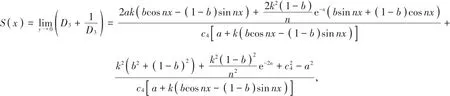
则

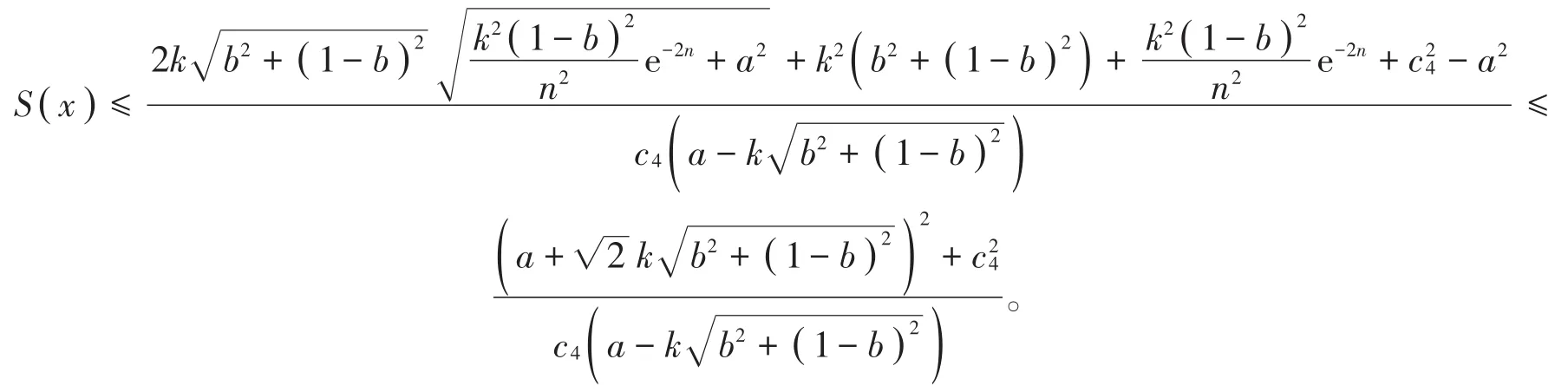
注意到，上面的定理给出的是最一般的情况，并没有对边界点进行固定，下面我们固定实轴上0,1与∞三点，有下面的结论。

推论1设

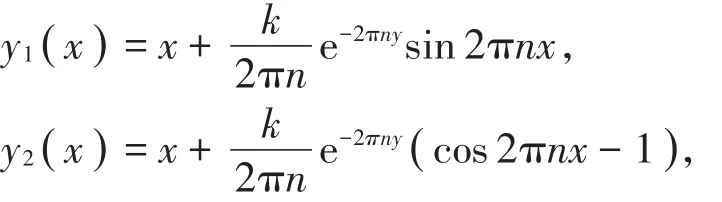
n∈N*,0≤k＜1,y(x)=y1(x)+y2(x),c5＞1，

则y(x)由上半平面到其自身的调和拟共形延拓表达式为

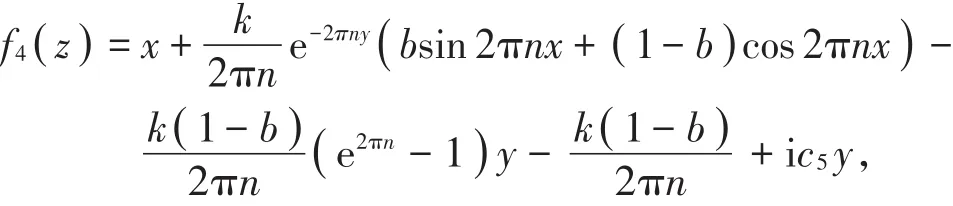
其伸张函数有估计式

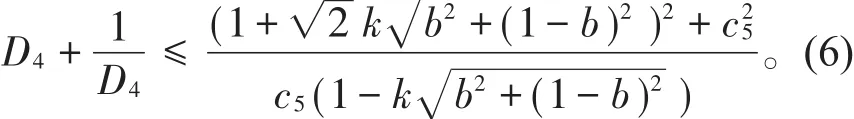
证明 由定理3的计算方法和定理4的结果很容易证得(6)式。

注 对于推论1中的y(x)，任意的x∈R，t＞0，根据拉格朗日中值定理和

可知，

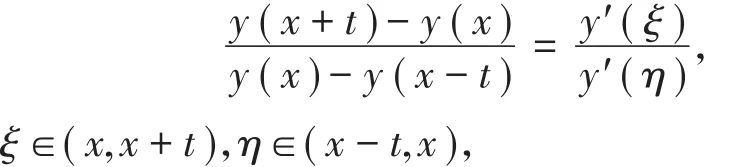
即y(x)是

拟对称函数，可以作Beurling-Ahlfors延拓。