基于用户分组的多用户偏好查询
2018-09-07王沁雪江国华秦小麟
王沁雪,江国华,秦小麟
(南京航空航天大学 计算机科学与技术学院,南京 210016) E-mail:nuaawqx@163.com
1 引 言
随着基于位置的服务(LBS)、移动互联网等技术的迅速发展,人们的生活越来越呈现出群体性、交互性和协作性的特点.越来越多的用户更青睐于同具有共同偏好的其他用户共享资源,在满足自身需求的前提下,提升使用资源的性价比,例如用户会选择拼车或拼团旅行以降低行程花销.与直接向每个用户提供查询结果相比,先对用户分组,再对每个分组提供查询结果具有如下两方面的优点:一是对于查询用户,将用户同与其相似或是满足其偏好的用户划分为一组,由于提前考虑到了其他用户会对该用户满意度产生影响,从而最终会使用户体验提升,同时分组会使查询效率提高;二是对于被查询对象,在同一时间为具有相似的属性或偏好的多个用户提供服务,可以提高服务的有效性及高效性.
例如,系统中有多位用户发起拼车请求,若采用传统的查询方法需要将每位用户的查询都执行一次,且用户最终可能与任何人成为拼车伙伴.提前分组则会对用户最终的拼车同伴进行筛选,从而提高了用户体验,且以组为单位进行查询也提高了查询效率.因此,在类似查询情境下,首先对用户进行分组是十分必要且有意义的.整个查询可分两步实现,即首先对查询用户进行分组,再以每组为单位进行查询.
如何将用户进行分组是处理以上问题关键的一步,合理地分组可以在很大程度上提升用户体验以及查询结果集质量,目前已有很多建立在用户分组之上的研究,如组查询、组推荐等[1-3,12].在这些研究中,对用户分组的依据往往是某些用户具有类似的查询任务、相同的偏好或是相同的属性,它们多是以提高最终的查询结果质量为目的来进行分组.然而在一些实际问题中,应用上述分组方法存在一定缺陷.比如在拼车、拼团旅行中,用户需要与同组成员进行协作与交流,而并不是简单地利用对方得到一个查询结果.用户在被分组后将会一起行动,他们所在意的内容不仅仅是他们这项活动的目的以及通过结成分组能否从中受益,也会关注同组的伙伴是否令自己满意.因此在建立分组的过程中,除了要考虑用户对于查询对象的偏好,也要考虑用户与同组伙伴对于相互间的偏好.
考虑这样一个场景:系统中多个用户发起拼车请求,系统对用户发起的查询进行分析并将用户分组,分组后为每组派发出租车.在分组的过程中需要考虑每组用户的起点与终点是否接近,以及他们对出租车偏好是否相同,比如距离相近的几位用户都希望坐无烟的出租车,则将他们分为一组并为其分配无烟车.同时,为了使行程舒适,各个乘客也应该对彼此感到满意.
很多已有的分组算法仅考虑将属性相同的用户分为一组[8,9],但显然不能满足该场景的需求.如A、B两个用户都是吸烟的男性,若在分组中只考虑用户属性是否相似,他们会因为属性相似而被分为一组.但是,如果A、B两人都希望与不吸烟的女性组成一组,他们都会违背对方对于同组用户的偏好要求,从而导致用户体验较差.也有算法通过衡量用户间查询偏好的差异来对用户进行划分[6,7,10],将偏好相似度高的成员放在一个组内,但同样无法满足该场景的分组要求:A、B这两位用户对同乘用户的偏好都是女性、不吸烟,两人偏好一致因此被分到一组,然而他们本身的属性却违背了对方对于同组用户的偏好要求.
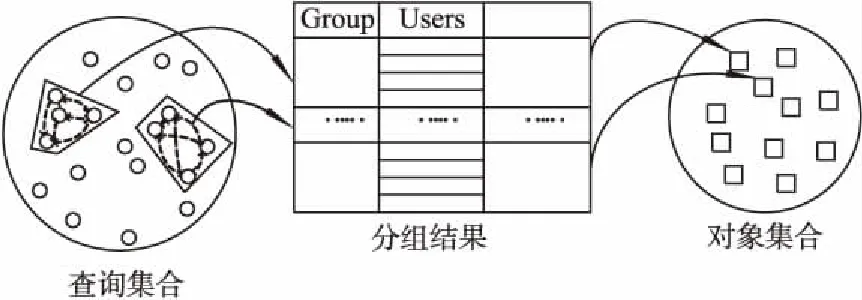
图1 多用户分组查询示意图Fig.1 Diagram of multi-user group query
图1给出了多用户分组查询流程的示意图.上述问题可以概括为:对于某对象集合,系统中同时存在多个用户的偏好查询,在查询过程中需要将用户进行合理分组,每组用户得到同样的查询结果.目前有关分组的解决方法并没有考虑到组内成员之间的相互偏好.基于以上考虑,本文的工作主要针对多用户如何在合理分组的基础上进行偏好查询,提出一种基于用户分组的偏好查询算法PQBG(Multi-users Preference Query Based on Grouping Algorithm),主要贡献如下:
1)研究多用户查询系统中组查询的问题,分析在查询前对用户进行分组的优势,提出传统对用户进行分组的方法在应用于该问题上的不足,即未考虑组内用户对相互间偏好的因素,并分析其对查询结果的影响.
2)给出分组标准,并提出了一种基于用户分组的偏好查询算法PQBG,该算法将查询分为分组和查询两个阶段,并在分组过程中加入了对组内用户之间偏好需求的考虑.
3)将PQBG查询算法与未将用户进行分组的算法BKNN,以及两个分组查询算法GAA、GAPS进行对比,采用扩充后的真实数据集对算法性能进行评估.实验结果表明,PQBG算法能提升解决多用户偏好查询问题时的结果质量.
2 相关工作
对用户进行群组划分常用于组查询及组推荐系统中,但在大多数情况下是在假设群组划分已经给定的情况下进行下一步[1-3],涉及到具体如何分组的研究较少,而多用户偏好查询过程中如何对用户进行合理分组是本文的研究重点.分析已有研究查询或推荐系统等工作中的群组划分依据,可分为如下四类:
1)地理位置.利用地理位置或轨迹信息将用户进行分组,最简单的方法是将某一区域按照经纬度以一定的步长栅格化,将落在同一栅格内的用户划为一组.张潮等人在[4]中将具有相同轨迹信息的用户划分为一组,利用单个用户作为代表群组中具有相似运动轨迹的用户以降低位置更新次数.文献[5]也研究了从轨迹信息中发现旅行同伴的问题,并提出了智能交集和闭合候选的策略以减少内存成本.
2)社交关系.在对社交网络的研究中主要是利用用户之间的社交关系对用户进行分组[11].Yang D N等人将社交关系定量地表示为社交距离,利用社交距离与熟人约束,以从社交网络中找到一个给定成员数目以及指定活动时间的分组[14].文献[15]同时考虑社交距离与空间距离,提出查询k-CoFQ,最终得到的用户分组中的成员彼此之间存在紧密的社会关系,并且被限制在地理空间中的一个小区域.
3)用户属性.一些研究根据用户的社会化属性、人口统计学特征以及用户本身的各种属性(如年龄、职业等)对用户进行分组.如Gu L等人在[8]中充分利用了用户的社会信息,提出一种考虑潜在用户分组信息的相似度度量方法,以计算用户潜在的分组.文献[9]中在分组时利用了人口统计学特征(如儿童、残疾人等),将用户划分为需要特殊对待的不同组.
4)用户偏好.这种分组方法常用在推荐算法中,利用用户的偏好对用户进行分类,群组的偏好相似度越高,生成的群组推荐结果集越令人满意[7,13].如Boratto等人在[6]中通过计算用户偏好相似度构建用户相似度网络,利用社区划分算法对用户相似度网络进行划分.[10]通过建立用户对对象的评分矩阵并计算用户之间的欧氏距离,对相同项目具有相似评分的用户会被划为一组.
通过总结得出,以往研究中对用户分组的目的大多为了提高查询结果质量,或是提高查询效率,但均没有考虑到分组中用户之间存在交互与协作的情况.除了没有考虑到用户对于同组伙伴的偏好之外,大部分研究在分组过程中对组内人数也没有限制,只要符合要求便划作一个组,这在很多组内人数存在上限的情境中无法适用.本文提出PQBG算法解决上述问题.
3 基于用户分组的多用户偏好查询算法
3.1 问题描述
多位用户提出偏好查询,其中偏好包含了对查询对象的偏好和对其他查询用户的偏好.查询算法分为分组和查询两个阶段.在分组阶段,算法解决如何将N个查询用户分为M组的问题,每组人数最多为v,这些组之间没有交集.分组结果需要满足三点:一是组内用户属性相似;二是组内用户对查询对象的偏好相似,三是同组中每位用户对其它用户的偏好都能得到满足.在查询阶段,查询对象的属性与查询用户偏好属性相似度越高,其越有可能出现在查询结果中,最后每组查询用户得到评分最高的k个查询对象.
以用户拼车为例,每位用户对于查询对象出租车和拼车伙伴都存在偏好,如对出租车的偏好为信用评分在9分以上,司机为不吸烟的男性,对拼车伙伴的偏好为信用评分在8分以上,不吸烟的女性.系统分析用户查询,通过用户的属性及其偏好分组.PQBG算法主要应用于拥有基于位置服务的应用,因此其地理位置,即空间属性是一个重要的影响因素.对于该类应用,在进行分组时,首先应保证可能成为一组的用户地理位置相距不远,因为即使其他偏好条件都完全符合,司机要跨越整个城市去接几名乘客是不现实的.其次,同组成员对出租车的偏好应在最大程度上接近,比如都希望乘坐不吸烟的男司机开的车.最后,组内成员对相互间的偏好不能发生冲突,如用户在找到他所希望的信用评分在8分以上,不吸烟的女性同伴时,他本身的属性也需要满足同伴对他的偏好要求.在分组结束后,计算每辆出租车相对于该组的评分,并为每组返回评分最高的k辆出租车.
3.2 基本定义
定义1.(对象集合)对象集合O={o1,o2,…,om}.oi={ID,pos,X1,X2,…,Xl},(i=1,2,…,m)代表一个对象.其中ID为主键表示元素ID,pos表示对象的空间属性,若对象属性集中不包含空间属性,则其pos为空;Xt(t=1,2,…,l)表示对象的其他属性,数据类型为浮点数.
定义2.(查询集合)查询集合G={u1,u2,…,un},ui=
定义3.(用户分组)分组group={u1,u2,…,us|ui∈G,(i=1,2,…,s)},(s≤n),表示一组用户的集合.
定义4.(运算符⊙)ui.Pt⊙uj.Pt表示用户ui和用户uj对查询对象属性Xt偏好Pt的偏好重合度,取值为[0,1].
若Pt为范围偏好(如评分为[8,10]),则
(1)
若Pt为布尔值(如性别为女,设定性别为男用1表示, 性别为女用0表示),则

(2)
定义5.(偏好相似度)相似度函数sim(ui,uj)表示用户ui和uj关于查询对象的偏好相似程度,计算公式为:
(3)

定义6.(组偏好集合)在一个分组group={u1,u2,…,us}中,组偏好集合D={M1,M2,…,Mh},其中Mi=u1.Qi∩u2.Qi∩…∩us.Qi,i=1,2,…,h,即组内所有成员对群组其它元素偏好集合的交集.
定义7.(组属性集合)在一个分组group={u1,u2,…,us}中,组属性集合A={N1,N2,…,Nh},其中Ni=u1.Yi∪u2.Yi∪…∪us.Yi,i=1,2,…,h,即组内所有成员属性值的并集.
定义8.(对象评分函数)S(ui,oj)表示用户ui对对象oj的评分.当二者空间属性存在时评分包含两个方面,一是ui与oj的空间属性相近,二是oj属性与用户ui对查询对象属性偏好的相似度高,使用λ来对两者进行平衡,在本文中默认为0.5;若ui与oj不存在空间属性则λ的值为1.具体表示为:
(4)
其中contain(ui.Pt,oj.Xt)表示oj的第t个属性是否与ui对其的偏好范围存在交集,若存在则函数值为1,若不存在则函数值为0.d(ui,oj)表示ui与oj的距离,dmax表示ui与查询集合中对象的最远距离.
以拼车场景下的用户查询以及车辆信息为例.表1为出租车属性表,o=(1,189.791856,31.243058,7,9.1,1,0)代表一辆出租车,ID=1表示出租车ID为1,pos=(189.791856,31.243058)表示该车所在位置的经纬度.后四个数值分别表示出租车(New,Credit,Sex,Smoke)四个属性的值.
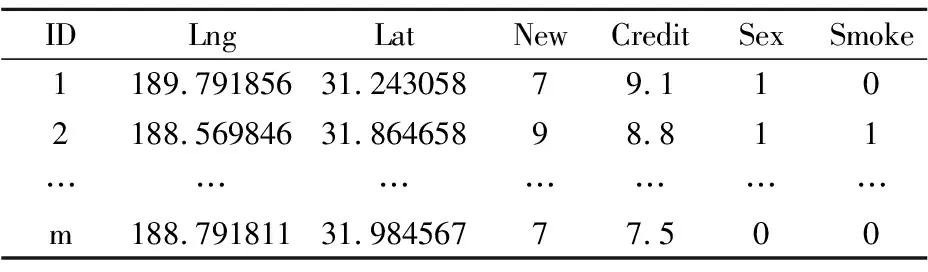
表1 出租车属性表Table 1 Attribute table of taxi
表2为用户属性表,表3为用户偏好表,u1=<(1,188.791856,31.943058,188.797638,32.028402,9.5,1,0),([6,10],[9,10],U,{0}),([8,10],U,{0})>代表了一个查询.其中,u1.Attr=<(1,188.791856,31.943058,188.797638,32.028402,9.5,1,0)表示用户属性集,该用户ID为1,起点经纬度坐标为(188.791856,31.943058),终点经纬度坐标为(188.797638,32.028402),该用户的其它属性为信用值9.5,不吸烟的男性.u1.Obj=([6,10],[9,10],U,{0})表示用户对查询对象的偏好,他希望出租车在六成新以上,司机的信用评分高于九分且不吸烟,性别偏好为U表示该用户对司机的性别没有特殊要求.u1.Par=([8,10],U,{0})表示用户对其他用户的偏好,他希望和信用值大于8,且不吸烟的人成为拼车伙伴.
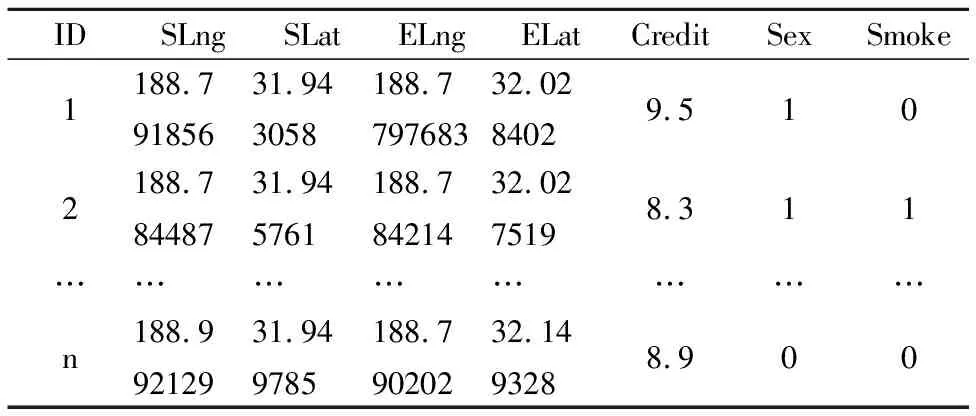
表2 用户属性表Table 2 Attribute table of user
若有另一位用户发起查询,u2=<(2,188.784487,31.945761,188.784214,32.028519,254,8.3,1,1),([9,10],[8,10],{0},{0}),([7,10],{0},{0})>.利用公式(3)可得出两位用户的偏好相似度为sim(u1,u2)=0.6875.若将两位用户划为一组,则该组的组偏好集合为D={[7,10],{0},{0}},该组的属性集合为A={{9.5,8.3},{1},{0,1}}.

表3 用户偏好表Table 3 Preference table of user
3.3 PQBG算法
本节给出基于用户分组的多用户偏好查询算法PQBG.查询集合G={u1,u2,…,un}发起对对象集合O={o1,o2,…,om}的查询,在查询过程中利用PQBG算法对查询信息进行分析,将查询集合中的用户分组,其中每组成员人数最多为v,并为每组返回按评分函数排序的前k个查询对象.
PQBG算法输入为系统中的查询集合G、查询对象集合O、每组人数上限v与结果个数k,输出为最符合组偏好的top-k对象集合result.首先选取系统中最早发起查询的用户作为分组的起点用户,计算该用户与其它用户的欧氏距离,并选取前K名用户作为预选结果集.之后计算这K名用户与起点用户对查询对象的偏好相似度,生成按偏好相似度降序排列的队列L.接着为每组设定组偏好集合及组属性集合,利用这两个集合对队列中的用户进行筛选,从队头用户起依次筛选,满足条件的用户可加入该分组;重复上一步,若每组达到人数上限v则停止;若遍历K个用户组内人数仍无法达到v,则认为没有足够多的用户满足小组要求,组内所有人数即为该组最后的总人数.最后利用该组的查询偏好集合得到该组的查询结果集合.PQBG算法执行一次结束后,重新计算系统中的查询集合,利用该算法生成新的分组并为该组返回查询结果.
算法1.PQBG算法
输入:查询集合G={u1,u2,…,un},查询对象集合O={o1,o2,…,on},每组人数上限v,输出结果个数k
输出:最符合组查询偏好的top-k对象集合result
1.while(G≠∅)
2. startuser←earliestStart(G);
//将等待时间最久的用户选作起点用户
3. group.add(startuser);
4. G.delete(startuser);
5. get the KNNresults of G and keep them in preResult;
// 利用K近邻查询算法处理生成预选结果集
6. preList←DesSimilarity(startuser,preResult);
//依次计算起点用户与预选组员的偏好相似度,将结果按降序排列
7. group←UserSelect(startuser,preList,v);//利用组偏好集合与组属性集合筛选用户生成分组
8. result←TopkPreQeury(group,O,k)//返回该组查询结果集合
9.returnresult;
PQBG算法中主要的四个模块分别为预选结果集生成(第1-5行),预选队列生成(第6行),组员选择(第7行)以及查询结果生成(第8行).在3.3.1至3.3.4中详细分析了这四个模块.
例如在拼车场景中,PQBG算法首先选取起点用户,计算他与系统中其他用户的欧氏距离并取前K个用户.之后分别计算这K个用户与起点用户对出租车的偏好相似度,用户按偏好相似度降序排列.接着以起点用户为中心建立分组,设定组偏好集合并将其初始化为起点用户对其它用户的偏好,设定组属性集合并将其初始化为起点用户的属性.从队首用户起依次判断每位用户的属性和偏好是否与小组已有成员相冲突,无冲突则加入该组并更新组偏好集合与组属性集合.遍历队列,直至组中已有v名成员或遍历完队列中所有用户.最后计算出租车相对于该组的评分,得到最优的k个查询结果.
3.3.1 预选结果集生成
为提高组员选择效率,节约系统开销,设置组员预选步骤.利用K近邻查找方法思想,计算用户之间的欧氏距离,距离越近则二者越相似,越有可能被归为一组.带特征权参数的两个n维向量的欧氏距离计算公式为:
(5)

在此前对各属性值进行归一化处理,m为查询个数,将原始数据都归化为[0,1]区间的数,运用公式:
i=1,2,…,m,l=1,2,…,n
(6)
为了提高查找效率,采用kd-tree作为索引.计算结束后选取距离最近的前K名用户作为预选组员.
如在拼车场景下,查询用户都具有空间属性,且该类属性对于计算欧式距离起到了决定性作用.直观上认为出发点与目的地都越接近的用户越有可能成为同组伙伴;该组发起者是等待时间最长的用户,同时也希望系统中等待时间久的用户优先加入分组.因此考虑五个属性参数:起始点经度、起始点纬度、终点经度、终点纬度、查询等待时间.同时,在考虑两个用户是否相近时,其起始点与终点距离远近的重要性远大于其等待时间的长短,因此在该场景下公式(5)的默认权重为(0.24,0.24,0.24,0.24,0.04).若应用于查询用户不存在空间属性的场景,预选结果集生成算法同样适用,此时计算欧式距离只考虑时间属性这一维属性,其权重为1.
3.3.2 预选队列生成
预选队列通过计算预选结果集中成员与起点用户对查询对象的偏好相似度得到,偏好相似度定义及计算公式已在定义5中给出.生成预选队列是为最终的组员确定做准备,该步骤对最终的组员确定顺序进行排序,查询对象偏好越相似的用户越被优先考虑是否能成为同组成员.分别计算预选结果集中用户与起点用户对查询对象的偏好相似度(第1-3行),在组内成员对相互间偏好不冲突的前提下,他们对查询对象的偏好越相似越优,因此生成的队列是由按用户偏好相似度大小降序排列(第4-5行).
算法2.预选队列生成算法DesSimilarity
输入:起点用户startuser,预选结果集preResult
输出:按偏好相似度降序排列的队列preList
1.foreach tupleuin preResultdo
2.u.sim=sim(startusers,u);//计算偏好相似度
3.endfor
4. preList←descendingOrder(preResult);
//将预选结果集按偏好相似度降序排列
5.returnpreList;
3.3.3 组员选择
算法3.组员选择算法UserSelect
输入:起点用户startuser,按偏好相似度降序排列的预选组员队列preList,每组人数上限v
输出:生成成员数最多为v的分组group
1. GroupPreSet.add(startuser.Par);
2. GroupAtrrSet.add(startuser.Atrr);
3. GroupNum=1;
4.foreach tupleuin preListdo
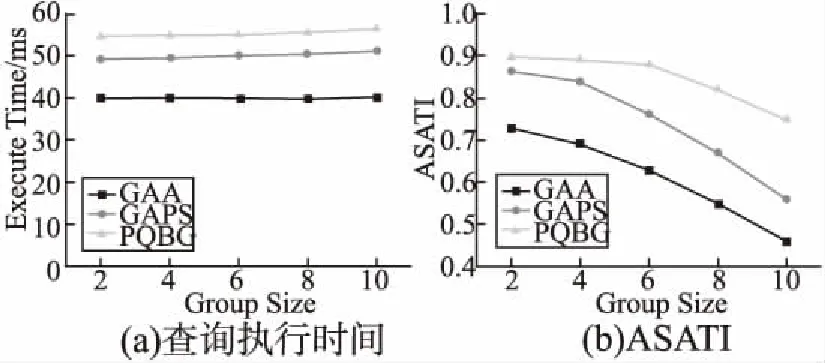
5.if(GroupNum 6. ConfGroupPreSet=U.complement(GroupPreSet); //计算组冲突偏好集合 7. u.ConfPar=U.complement(u.Par); //计算用户的冲突偏好 8.if(conflict(u.Atrr,ConfGroupPreSet)=0) &&(conflict(GroupAtrrSet,u.ConfPar)=0) //判断用户与组成员之间是否冲突 9. Group.add(u); 10.G.delete(u); 11. GroupNum++; 12. GroupPreSet.add(u.Par); 13. GroupAtrrSet.add(u.Atrr); 14.endif 15.endif 16.endfor 17.returngroup; 组偏好集合与组属性集合意在维护新用户与组内已有用户无冲突,这里冲突是指每名用户的属性是否满足组内其它组员对用户的偏好.初始化组偏好集合为起点用户对其它用户的偏好,组属性集合为起点用户的属性(第1-3行),从预选组员队列头起依次判断队列中的用户与这两个集合的冲突情况(第4-5行).为了提高算法效率和减少比较次数,计算用户偏好在其值域范围的补集,为用户的冲突偏好;计算组偏好集合在其值域范围的补集,为组冲突偏好集合.此时,只要存在某一属性维度的值与对其相应的冲突值域交集不为空,则表示存在冲突,该用户不能加入分组.若组属性集合与该用户的冲突偏好不存在交集,且该用户的属性与组冲突偏好集合不存在交集,则将用户加入该组的结果集,并将其从原始查询集合中去除,目的是保证每个小组之间不存在交集(第7-11行).加入后更新该组的组偏好集合,为新用户对其它用户的偏好集合与原来组偏好的集合交集;更新该组的组属性集合,为新用户属性与原来组属性的集合并集,并返回生成的组(第12-17行). 3.3.4 查询结果生成 在生成用户分组的基础上,给出最终的查询结果生成算法.本文定义的研究对象与空间关键字查询类似且查询重点为分组算法,因此在查询时借助空间关键字查询中的BKNN算法[17,18],将整组视为一个查询点,利用该组的查询偏好集合及属性集合得到该组的查询结果集合.首先将整组成员的平均位置信息设为查询点的位置信息(第1-4行),并将该组的组偏好集合设为查询点的偏好信息(第5行),最后利用BKNN算法得出前k个查询结果(第6-7行),这k个对象不仅满足该组的查询偏好且距离平均查询点最近. 算法4.查询结果生成算法TopkPreQeury 输入:用户分组group={u1,u2,…,us},查询对象集合O={o1,o2,…,on},输出结果个数k 输出:最符合组查询偏好的top-k对象集合result 1.forall tuples uiin groupdo 2. pos=AddPosition(ui.pos); 3.endfor 4. q.pos=Average(pos);//计算组成员平均位置 5. q.per=GroupPerSet; 6. result←BKNN(q,O,k); 7.returnresult; 本章实验验证PQBG算法的有效性及查询性能,与BKNN、GAA、GAPS三个算法进行对比.其中BKNN算法[18]不对用户进行分组,针对单个用户,直接利用对查询对象的评分得出评分最高的k个查询结果,假设得到相同top-1结果的用户最终为同组成员,每组人数最多为v;GAA与GAPS算法是作为对比的Baseline算法,这两个算法都对发起查询的用户进行分组,其中GAA算法仅选取与起点用户欧氏距离最近的v-1名用户作为同组成员;GAPS算法在预选队列生成后,直接选取前v-1名用户作为同组成员,而不考虑组内成员相互间的偏好情况.四个算法的比较如表4所示.实验环境为:Inter(R)Core(TM)i3-2120 CPU@ 3.30GHz,4BG内存,Windows 7操作系统.所有算法均是采用C++语言实现,编译器为Visual Studio 2013. 表4 PQBG算法与BKNN和Baseline算法的比较Table 4 Compare with PQBG,BKNN and Baseline 算法的有效性通过定义SATI值对用户满意度进行评估.在查询结束后,设每组最终人数为s(s≤v),则组内每位的用户ui的SATI值通过四个因素进行度量:与同组成员间平均属性相似度、与同组成员间平均属性及偏好相容度、组饱和度、查询结果评分.分别用Ai、Fi、Ni、Si表示,它们的值域都为[0,1].定义如下: Ai表示用户ui与同组成员间的平均相似度,是该用户与组内其余成员欧氏距离的平均值,计算公式为: (7) Fi表示与同组成员间平均属性及偏好相容度,计算公式如公式(8).其中contain(ui.Qt,uj.Yt)表示用户uj的第t个属性是否与ui对其的偏好范围存在交集,若存在则函数值为1,若不存在函数值为0. (8) Ni为组饱和度,为组内最终人数与组人数上限的比值.Si为用户查询结果评分,其计算方法如公式(4)所示. 由以上四个参数得到用户SATI值计算公式: SATI=α.Ai+β.Fi+γ.Ni+εSi (9) H名查询用户的平均SATI值ASATI为: (10) α、β、γ、ε表示这四个度量因素在最终的用户满意度评分中所占的权重,默认值都设定为0.25.SATI值域为[0,1],其值越大,表示该用户对查询及分组结果的满意度越高.ASATI值越高,表示用户的平均满意度越高. 实验数据采用NYC′s Taxi and Limousine Commission网站公布的TLC Trip Record Data数据集.该数据集收集了纽约市2009到2016年的出租车行车信息,每条包含出租车出租等级、执照号、起点经纬度、终点经纬度等19项信息,从中提取2016年11月中的10571辆出租车信息作为实验的数据.由于该数据集中并不包含出租车的其他属性信息,如司机性别、吸烟与否等,实验通过随机采样生成的方法对原数据集进行了扩充,随机生成了出租车的其它属性信息.同时,在此基础上模拟生成了用户数据集,该数据集内每行信息包含了用户起点与终点的经纬度,并补充了用户的其它属性信息以及偏好信息. 图2 查询对象规模对算法性能的影响Fig.2 Performances with query object size 实验的主要目的是,将考虑组内成员存在偏好的分组查询算法PQBG与不考虑对组内成员存在偏好的分组查询算法GAA、GAPS,以及不对用户分组的普通查询算法BKNN进行比较,从而证明对用户进行分组,以及在分组的过程中加入对组内成员偏好考虑的重要性.第一组实验对分组查询算法(PQBG、GAA、GAPS)与不对用户进行分组的查询算法BKNN的查询性能进行对比;后三组实验对三个分组查询算法(PQBG、GAA、GAPS)的查询性能进行对比.实验结果均是算法执行1000次的平均性能. 4.2.1 查询对象规模对算法性能的影响 为了分析查询对象规模对算法性能的影响,实验在查询对象个数从2K到10K下进行实验.系统中查询用户个数为3K,分组查询算法中组规模大小为4,K值取30,计算系统中所有用户查询完毕后的查询时间与用户平均满意度ASATI. 图2显示了查询对象规模对算法的执行时间与ASATI值的影响.在查询规模较小时,分组代价相对较高,因此BKNN的查询执行时间相对较低.随着查询对象规模的增大,查询耗时逐渐高于分组耗时,因此BKNN的查询时间增长速度高于三个分组查询算法,最终所需查询时间高于分组查询算法.即随着查询对象规模的增长,以整组为单位进行查询,代价将低于每个用户单独进行查询.而在ASATI值方面,由于BKNN算法未曾考虑用户属性及偏好,其Ai、Fi值远小于三个分组查询算法,因此ASATI值始终最小,且由于组饱和度下降,总体呈下降趋势.而三个分组查询算法随着查询对象规模增大,Si有所提升,ASATI呈缓慢上升趋势. 4.2.2 K值对分组查询算法性能的影响 从上节实验中发现,分组查询性能总体上要优于普通查询,因此后三节针仅对三个分组查询算法(PQBG、GAA、GAPS)进行性能比较,查询对象为整个数据集.由于在实际情况中,系统中的查询用户规模以及查询对象规模在不断变化,因此三个实验考察在某一时刻算法生成一个新的分组并得出该组查询结果的性能. 图3 K值对算法性能的影响Fig.3 Performances with different K 图3显示了在查询用户数为3K,组规模为4时,K的取值对分组查询算法的执行时间与ASATI值的影响.随着K值的增大,算法的执行时间都随之增大,其中GAPS算法由于存在计算用户的偏好相似度与生成预选队列的过程,执行时间要大于GAA算法.而PQBG算法在GAPS算法的基于组内偏好对组员进行筛选处理,因此执行时间最长.就ASATI值而言,GAA算法始终最低,因为GAA算法的Si值明显低于其它算法.值得注意的是,在K很小时其余两者的ASATI值接近甚至GAPS算法的ASATI值更高,这是由于当K值很小时,虽然采用GAPS算法建立的分组同组用户间属性及偏好相容度Fi较低,但采用PQBG算法的组饱和度Ni也很低造成的.随着K值的增大,采用PQBG算法的组饱和度增大,而采用GAA算法和GAPS算法建立的分组中同组用户间属性及偏好相容程度基本没有增长,因此PQBG算法的ASATI值将高于另两个算法. 4.2.3 组规模对分组查询算法性能的影响 为了分析查询组规模不同对分组查询算法性能的影响,分析K取值为30且查询用户数为3K,组规模增大时,算法的执行时间与ASATI值,实验结果如图4所示. 图4 组规模对算法性能的影响Fig.4 Performances with different group size 组规模的大小对于算法执行时间几乎没有影响,这是由于算法中组员选择的步骤对于整个算法的时间复杂度的影响可以忽略不计.GAPS与PQBG算法的执行时间会有略微提升,而GAA算法与组规模大小无关,因此执行时间基本保持不变.三个算法的ASATI值都会下降,这是由于随着组内成员的增多,同组用户属性相似度以及查询结果评分都会下降导致的.同时,对于GAA和GAPS算法,虽然组成员数可以一直达到饱和,但随着组内成员数的增多,同组用户间属性及偏好相容度下降加快.而PQBG算法随着组规模的增大,ASATI值的下降幅度由最初的较小突然变大,这是由于当组规模达到一定程度后,由于无法找到足够的组员,组饱和度的下降将导致的. 4.2.4 查询用户规模对分组查询算法性能的影响 图5 查询用户规模对算法性能的影响Fig.5 Performances with user size 文本从实际应用需求出发,研究基于用户分组的多用户偏好查询算法.在查询前对基于用户偏好对用户进行分组可提高用户满意度,如何对用户进行合理分组是解决该问题的关键,现有的分组查询算法在解决多用户偏好查询时,未考虑用户对组内成员之间的偏好对分组结果影响.基于此,本文提出一种考虑组内成员相互间偏好的分组查询算法PQBG.实验结果表明,PQBG算法能提升多用户偏好查询的查询性能.4 实验及分析
4.1 实验环境

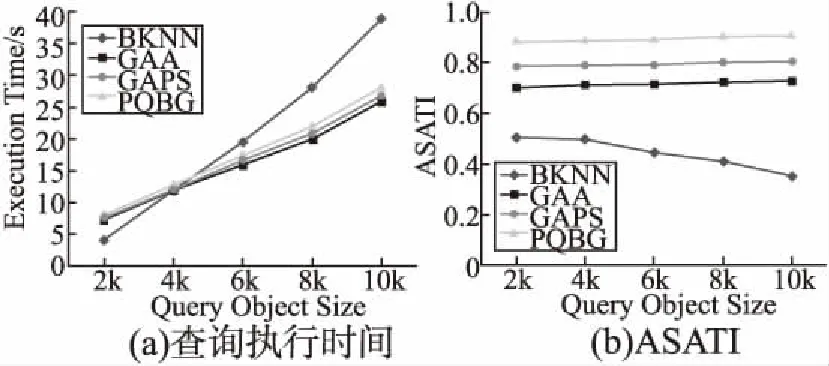
4.2 结果分析



5 结束语
