思维生长处的真合作——《真分数和假分数》的教学实践与思考

江苏南京市孝陵卫中心小学 张 蜜

缘 起

前段时间，笔者参加了南京市三城区连片教研活动，在同课异构中，所执教的《真分数和假分数》设计新颖、生成精彩。然而，在一开始试上的过程中，却不尽如人意。

看似简单的一节概念课，怎么能在40分钟的时间内上出新意？以学为中心的教学究竟要经历怎样的过程？哪种方式更能达到教学目标、体现数学思想呢？为此，笔者和所在的团队经历了试上、研磨和改进的过程。

试上中的困惑

笔者按照教材教学了例5和例6，先让学生分别用一个圆表示了四分之一、四分之三、四分之四，并理解了每个分数的意义；然后让学生用涂色的方式表示5个四分之一，初步理解四分之五；接着同样用涂色的方式表示，并在小组里交流例6；最后请学生按照分子和分母的大小关系分类，并揭示概念。

笔者试上时按部就班，规定了从分子和分母的大小比较去分类，所以学生没有太多的思考，更不会将图形和分数结合观察，这个现象导致学生被动接受。教师在处理时也过于急躁，分类出来后直接揭示概念。这样看似学生都会，其实思维已经僵滞。

接着，在练一练第一题“用分数表示涂色部分”中，此题（图1）学生的错误率极高，55%的学生都写成了八分之七。老师也做了预设，出示了下面那样的集合圈（图2），让学生对比区别，但学生并不关注“大括号”与“集合圈”的区别，然后老师告知学生“把许多物体看成单位1时，一般不会再把每一个去平均分”。这种解释的方式学生并不能够领会。

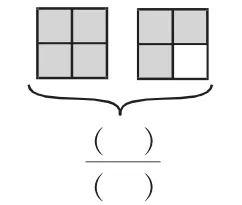
图1

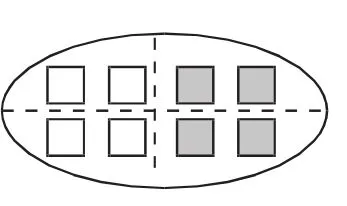
图2

研磨中的反思

课堂要想有新的突破，必须以学生的学为中心，深刻吃透教材，重新建构学习体系。

一、坚持自主合作的学习形式，培养深思的意识

因为考虑学生已学习了分数的基本知识，所以本节课在教学思路上突出学生学的过程，力求学生通过合作探索，对比、发现真分数和假分数的特点，并在思考的过程中比较准确地概括出真分数、假分数的意义。突出学生的合作意识，培养学生的数感，突出培养学生的创新精神和实践能力。

二、确立操作实践的学习主题，营造合作交流的氛围

实践是检验真理的唯一标准。实践操作是儿童智力活动的源泉，希望这节课能以实践操作为切入点，利用信息技术，从直观的图形入手，使抽象的概念具体化，对学生思维能力发展起着极大的推动作用，学生通过小组合作来观察、分类、交流等理解新知，在数形结合的基础上学生能具体地感受真分数、假分数。

三、利用合作中的动态生成，培养思维能力

练习中的那题到底是八分之七还是四分之七，试上时老师用扩线和集合圈来对比的效果并不理想。其实，纯粹老师解释学生未必能听懂，数学上很多东西都是这样，不是老师不会，也不是老师解释不清楚，而是用什么方式解释学生最容易接受，对学生冲击力最大。

带着这样的三点思索，便有了以下课堂内容的呈现。

改进中的呈现片段一：任务驱动下的真合作

师：（出示□/4）你觉得它有可能是四分之几？

生：四分之一、四分之二、四分之三、四分之四、四分之五……

师：（出示一张圆片）把一个圆片看作单位1，能用它表示出分母是4的分数吗？四人小组，每人表示的分数要与他人不一样。涂完之后，在小组里说说这个分数表示的意义。（指名一组汇报）

师：（课件出现学生汇报的四分之一至四分之四，见图3）继续观察，它们之间有什么相同之处？与前三个分数相比，四分之四有什么特别的地方？

师：老师有个疑问，刚才怎么没有人用这张圆片表示出四分之五呢？为什么？

师：很显然这已经超出了一个单位“1”的能力了，当一个人的能力有限时应该想到什么？和小组同学合作，用刚才表示出的这个分数一起来研究，看能不能表示出四分之五？（小组探究）

指名小组上台展示，学生能够展示出（如图4）两种方法在黑板上，并说说这里为什么表示的是四分之五。

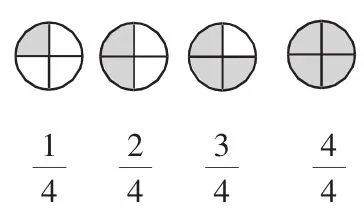
图3

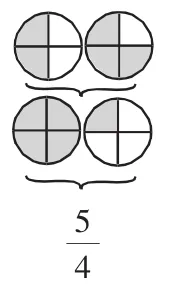
图4

【思考】四分之几，想一个分数，当一个学生说到四分之五时，有些学生惊讶：“啊？还有四分之五啊？”因为在有些学生的世界中，一个圆平均分，不管怎么分，怎么表示，它都没有超过单位1。这就是问题激活，学生的思维之门一下子被打开了，想去进一步学习。

接着学生动手操作，反馈都是四分之一到四分之四，得不到四分之五，通过这个现象，教师提问：“为什么没有人表示四分之五呢？”形成了问题意识，又形成了要研究的任务驱动。要想表示四分之五，这时1人手中的那个圆不够，需要合作，这种合作是真合作，在活动中进行了突破。前面四分之一到四分之四的复习变成了新学习的素材，出现了两种不同的方法：一种是第一个圆的四分之二和第二个圆的四分之三合起来，另一种是用四分之一和四分之四合起来。老师及时地把两种形式贴在黑板上，这个作品是学生合作出的作品，是新知识生长的地方，也是后面学习的需要。

片段二：合作中“分类多样化”渗透数学思想

师：（课件出示图5）仔细观察屏幕上的这些分数，你能不能按照一定的标准给这些分数分分类？（四人小组讨论分类方法）

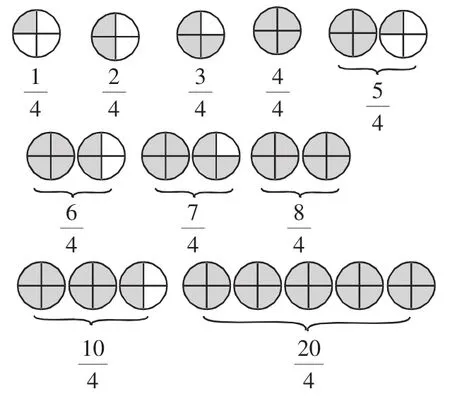
图5

生：我们小组是按照分子大于分母的一类，分子等于分母的一类，分子小于分母的一类。

师：他们是按照什么分类的？（根据学生回答，教师板书：分子与分母的大小关系）

师：这里的每一类都有哪些分数？（学生叙述，教师板书）

师：还有不同的分类方法吗？

生：我是看课件中的图形的，把用1个圆表示的放在一类，2个圆的一类，3个圆的一类，5个圆的一类。

师：那如果有7个圆、8个圆、10个圆的，岂不是我们要分好多类啊？在此基础上有没有更简单的分法？

生：这样可以将1个圆的分成一类，多于1个圆的分成另一类。

师：噢，我知道你是在和1的大小比较来分类的。（教师板书：和1的大小关系）

生：我还可以把涂满整个圆的放在一起，也就是分子是分母的倍数关系的分成一类，其他的分成一类。

师：分类是一种重要的数学思想方法，它给我们提供了进一步深入研究、学习的机会。这节课，我们重点研究按照分子与分母的大小关系进行的分类。这里的每一个类别你还能举例说出一些分数来吗？（学生回答，老师丰富板书）

师：其实，这些分数在数学上都有各自的名字，你们想知道吗？（学生翻开教材第59页，自学最后两行的内容，汇报真分数和假分数的定义，教师适时板书）

师：刚才在分类的时候，有同学提到了“与1的大小关系”。现在你们能结合课件图再来看一看，这些真分数、假分数与1相比各有怎样的关系？（学生回答，教师板书：真分数<1,假分数≥1。）

师：是否存在这样的关系，我们还将继续来学习！

【思考】在此片段中针对图5的分类，小组合作汇报想法，内涵丰富地展示了各种数学思想，如分类思想、比较思想、抽象思想、数形结合思想、归纳思想等。学生在交流分类时思维是开阔的，出现了各种方法，有分子与分母的大小比较，有与1的关系，还有与图形的个数做了比较。

我们在数学教学中经常会操作后比较，然后分类，得出结论。但常常是结论的意识很强，为什么会有这个结论，解释过程就比较弱了，用什么来解释就更弱。分类并不单纯为了获得结果，而是要体现学生怎么想的过程，促进学生间的相互学习。本片段中，有学生用以前学过的知识来解释，有通过操作过的学具和直观的演示解释，还有通过和别人讨论后形成观点。这个过程不仅是对分数意义的深度理解，对数形结合的一种分析，更使学生经历了用多样思维来分析和解决问题的全过程。

片段三：思维混乱处“合作作品”来纠错

对练一练第一题：“涂色部分可以用四分之七还是八分之七来表示？”指名2类不同填法的学生分别说出所填分数的道理，学生的争论焦点在于 “把谁作为单位1”，此时教师顺势引导学生看图2。

师：看这里，当时可没有同学认为这是八分之五哦！想一想，这里的四分之五是怎样产生的？

生：用1个圆表示的四分之四不够，再向另外一个圆借四分之一，合起来是四分之五。

师：这名同学关注了分数产生的过程，这里的大括号表示涂色部分的和。现在你知道把什么看作单位1了吗？

生：其中一个图形看作单位1。

对于下面练习学生便迎刃而解，真正弄懂了此类问题。

【思考】此片段中用了学生新授课时贴在黑板上的作品来解释，实践证明，用学生作品来解释学生问题最有力量，对他们的理解更有帮助。数学教学，其核心是培养学生的思维，学生合作时相互启发，生成出的各种“作品”为他们进一步学习铺垫了富有挑战性的互动环境，激发了学生的学习兴趣。

练习中如能充分利用生成的 “作品”，呈现学生的认知过程，能帮助他们真正高效地理解真分数和假分数的意义，突破了习题的难点，避免了很多错误，同时也体现了以学生为中心的课堂教学的价值。筻