从概念要素着眼，揭示面积概念的真义

山东临沂胜利小学（276000）

对刚学完“面积概念”的三年级学生进行测验，发现部分学生对面积概念一知半解。如，对“用什么形状的元件度量面积合适”认识不清，混淆周长和面积……

测验中有这样一道题：小黄用同样长的四根木棍围成甲、乙两个图形，那么（ ）。

A.甲比乙大

B.乙比甲大

C.一样大

D.无法比较

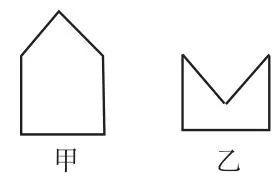
图1

一、对测验结果的分析

经认真研究和分析，我们一致认为这是学生认识的周长干扰了对面积认识的结果。有教师建议：“如果学生没学过周长，结果会好些吗？”于是，我们在二年级进行对照试验：在二年级A班采用举手表决的方式测试，结果全班都选A；在二年级B班采取单独问卷的方式测试，大部分学生选A。

这个结果很有趣：原来，学习知识多了还真能影响人的判断。因此，教学面积概念要抓住三要素：图形应封闭，无缺口，内容即为面积；面积大小与周线有关，周线越向四周扩张，面积越大；面积是可以随意划分为小块，然后密铺累加。

二、围绕两大基本要素展开的教学设计

围绕着面积概念三要素，我们设计了新的教学环节。

【要素一】封闭

片段1：暴露已有认知

师：举例说明什么是面积。

生1：教室地面的大小就是占地面积。

师：请指出教室地面的面积。

师（虚指一片区域）：这是教室的面积吗？

生2：太少了。

师：到底哪里是教室地面的面积？

生3：是所有铺着水磨石的地面。

在师生对话中能够暴露学生的原始经验，但这经验感知是模糊不清的，表现在学生无法正确表述教室地面的面积。

片段2：体会图形要封闭

师：几何图形的面积又指的是什么？

生1：图形内部（边界以内）的大小是面积。师：非常好。下面这些图形都有面积吗？

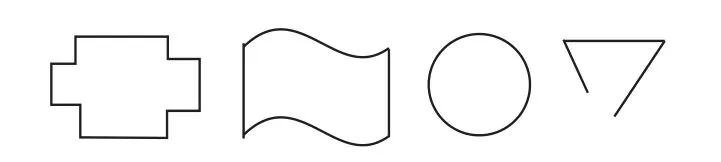
图2

（学生认为除了最后一个，其余图形都有面积。课件演示：给前三个图形内部涂色，并移除边框）

师：最后一个为何无面积？

生2：因为它有一个缺口，没有封闭。

师：没有封闭，能提取出面积吗？

生3：不能。

师：封闭图形的大小就是图形的面积。

【要素二】面积与周长有关系

片段1：探寻周长与面积之间的一般关系

师：猜想一下，被挡住的两个矩形（如图3，只露出部分）哪个面积大？为什么？

图3

生1：两个图形露出了宽，但上面的矩形可能会很长，远远超过下面的，这样一来，周长反而大一些。假如这样，面积也要大一些。

（课件演示：撤除遮挡物）

图4

师：比较下列各组图形，谁的面积大？

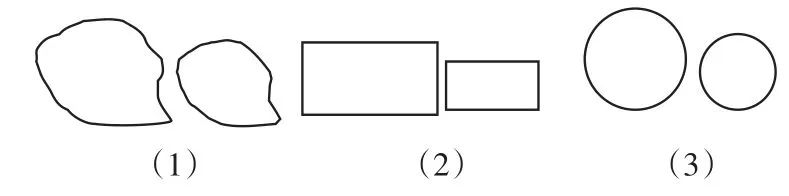
图5

师：谁能说说周长和面积之间的关联？生2：周长长的面积大。

片段3：探求周长面积之间的非一般关系

师：观察下述变化，你有什么发现？

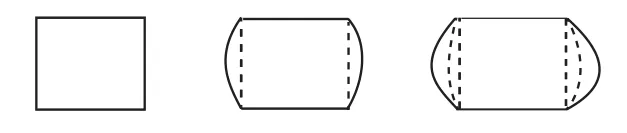
图6

师：再看看下述变化，又有什么发现？

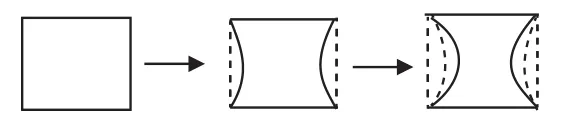
图7

师：再观察下述变化，这次又有什么发现？

图8

师：那么，之前的结论“周长越长，面积越大”对吗？再看这两个图，分割后的两个图形，面积和周长有什么关系？

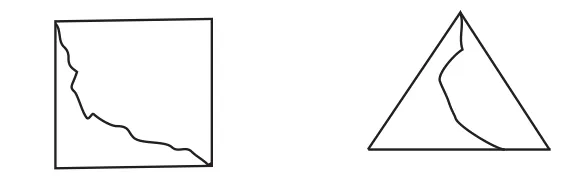
图9

为了厘清周长与面积的真实关系，观察活动分为两个层次，先是得出“周长越长，面积越大”的一般性规律；然后推翻和破除前述结论“周长越长面积不一定越大”——“周长变大，面积可能变小”“周长不变时，面积也会变大变小”等。通过揭示周长与面积的区别与关联，加深学生对面积概念的认识。

三、揭示面积单位的工具性和来历

【要素三】面积需要密铺

与“面积测量”结合起来：通过比较面积大小，创造“单位面积（工具）”，接着通过筛选各种面积单位卡片，确定“正方形”最合适。

师：比较图10中两个图形的面积。

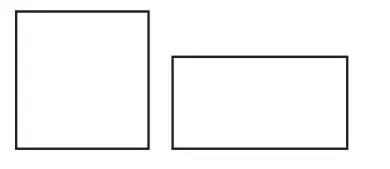
图10

图11

生1：重叠（如图11）。我认为正方形大。

生2：可用固定面积的小方块来密铺，看它们分别需要铺满多少个方块。

（教师提示学生找到合适的方块，学生测量后汇报）

生3：用方块度量，一个铺满9个，一个铺满8个，正方形的面积大。

师：用这个的方法（课件呈现：正方形铺满9个小方块，长方形铺满4个小长方形）行吗？

生4：因为不知小方块和小长方形的面积规格，所以无法比较。

生5：应统一度量单位。

师：比较各种方块的形状，用什么工具合适呢？

生6：用正方形最合适，可以密铺。

这样一来，既让学生理解“密铺”的必要性，又为“面积单位”的推出埋下了伏笔。

综上所述，关于面积概念的教学，不能让学生死记硬背，应该设计直观的操作活动，引导学生紧密围绕其内涵逐层分析，让学生做到心领神会。