发现差异 和声发展——小学数学解决问题教学中的发现差异策略

重庆渝中区人和街小学（400015）

《基础教育课程改革纲要（试行》指出：教师应尊重学生的人格，关注学生的个体差异，满足不同学生的学习需求，创设能够引导学生主动参与的教育环境，调动学生的学习积极性，培养学生掌握和运用知识的态度和能力，使每个学生都能得到充分发展。由于学生的学习环境、学习动机、学习兴趣、智力水平等方面存在很大的差异，同一种学习方法不可能适用于每一个学生。对于不同的数学问题情境，学生给出的解题策略自然会有所不同。因此，教师要在解决问题教学中实施发现差异策略，并在有限的时间内增加每个学生的知识输入量，提高学生知识输入的效率，从而促进学生数学素养的提高。

一、认同差异

美国学者戴安荷克斯指出：“实施差异教学意指教师改变教学的速度、水平或类型，以适应学习者的需要、学习风格或兴趣。”由此可以看出，差异教学主要关注的是学生的基本差异，既关注整体学生的进步，又注重每个学生的提高；不刻意按照学习成绩进行分组，而主要根据学生的个性差异进行教学，从而提高教学质量；以尊重学生的个性差异为基础，在教学内容设计、教育过程实践、教育结果评估中遵循差异化原则，达到所有人都能通过教育实现发展和进步的终极目的。

差异既发生在学生之间，也发生在师生之间，甚至师生之间的微妙差异更值得重视。教师要细心听取每一个学生的意见，既要在不同的意见中发现差异，也要在意见似乎基本一致的情况下发现差异。

二、解决问题发现差异策略

（一）搭支架策略

搭支架策略是在建构主义思想指导下，基于学生的最近发展区，给学生相应的帮助，以促进他们全面发展的师生互动、共同建构的过程。在解决问题的过程中，学生审题的能力存在着一定的差异，而缩小这种差异尤为重要。

1.两问改一问

如三年级上册71页例8“妈妈买3个碗用了18元。如果买8个同样的碗，需要多少钱？”，对于不能理解题意的学生，可以采用“两问改一问”的方式，即先出示两个连续的问题：“妈妈买3个碗用了18元，一个碗需要多少钱？”“如果买8个同样的碗，需要多少钱？”，在学生解答后拿掉第一个问题，使之成为两步问题。学生在解答的过程中就懂得，要解答第二个问题，必须以第一个问题为条件，拿掉的第一个问题，实际上就是中间问题。这样将题目简化，把两问改成一问，降低学生理解题目的难度，帮助学生完成审题过程。

2.搭提问“支架”

如三年级上册72页例9“妈妈的钱买6元一个的碗，正好可以买6个。用这些钱买9元一个的碗，可以买几个？”在学生不能及时想到解题策略时，教师可以给学生搭“支架”——“先求什么？再求什么？”“6元一个是单价，6个是数量”或“用这些钱是哪些钱？”，让学生找到中间问题“这些钱的总数=单价×数量”。在谈话的过程中，教师引导学生分析数量关系，使抽象问题具体化，从而让学生找到解决问题的突破口，形成解题的思路，突破思维的局限。

在解决问题中可以用到的“支架”工具有反馈、暗示、指导、解释、示范、提问等。教师对于支架工具的使用要立足于学生的差异，因为一个问题之所以会成为问题，是因为学生对其予以回应。

（二）动静转换策略

“动”与“静”相互转换、有效结合，既是数学的重要思想，又是解决问题的重要方法。教师要适时、适当地引导学生在“动”“静”转换中解决问题。

【案例】在教学三年级下册84页计算简单的经过时间时，教师设置情境“火车9：00开，下午6点到站，要坐多长时间的火车？”，除了留给学生足够的时间进行思考，还准备了钟面、直尺等学具供学生选择，降低问题的难度。

1.以动思题，建立表象

学生在探究过程中有着不同的差异：部分学生能够通过拨动钟面数大格子。此时，教师可追问：“为什么从9开始数呢？”然后引导学生再次经历拨钟后数数的过程。这样，学生可以看到时间经过留下的痕迹，体验到时间的长短，从而建立起“经过时间”的表象，真正理解“经过时间”。

2.以静思题，直观方法

大部分学生能够利用12时计时法分段计算或运用24时计时法计算，因此，在学生交流完方法后，教师可追问：“为什么用12-9=3（小时），就得到了上午参观的时间？为什么结束时刻减去开始时刻就等于经过时间？”结合学生的汇报出示“时间轴”并进行演示，让学生在静态的“时间轴”上理解原理，并建立数学模型“经过时间=结束时刻-开始时刻”。

3.以动静结合思题，拓展思维

教师再次动态展示两个钟面“一是从早上9时到晚上9时，二是从早上9时到下午6时”，并提出问题：“还有其他想法吗？”有学生利用钟面时针旋转一圈的规律来解决这个问题：从上午9时到晚上9时，时针刚好走一圈，也就是12小时；下午6时到晚上9时，距离12小时还差3小时，12-3=9（小时），所以要参观9小时。一个动态的钟面，由动到静，锻炼了学生的思维，提高了学生解决问题的能力。

在解决问题的教学中，教师要给学生积累丰富的表象，鼓励学生个性化地去分析和解决问题，注重对不同声音的倾听，避免用自己的思维去压制和取代学生的思维，从而使学生的主体性得到鲜明的体现。

（三）等价替换策略

波利亚认为：“解题就是在原先隔开的事物或想法之间去找联系。”等价替换策略的模型是指对条件关系复杂，没有直接的方法可解的问题，可尝试按问题中表示“倍数关系”或“相差关系”的条件去假设和替换，得到一个答案，然后把答案代入问题中去验证。面对学生的思维差异，等价替换能把复杂的数学问题简明化，问题也就顺理成章地得以解决。

1.转化句型，理解含义

二年级下册“用除法解决问题”求一个数是另一个数的几倍，实际就是求一个数里面有几个另一个数，两者仅仅是换了个说法。教师可将倍的概念和除法的意义联系起来，引导学生学会用转化的方法将“一个数是另一个数的几倍”转化成“一个数里面含有几个另一个数”，从而使学生会用除法解决“求一个数是另一个数的几倍”的问题。虽然进行了等价替换，但句子含义没有改变，学生还更容易理解。

2.等价替换，建构模型

六年级上册“解决问题的策略——替换”一课的教学目标是让学生完整地经历倍数关系替换策略的形成过程。在理解“小杯的容量相当于大杯的1/3”这句话时，教师可组织学生画图、操作、叙述、推想、验证、比较、概括等，这样，学生自然会想到一个大杯的容量就等于三个小杯的容量，大杯的容量是小杯的3倍。学生等价替换的思想一触即发：把1个大杯换成3个小杯或者把6个小杯换成2个大杯就可完成替换。在这个过程中，教师要追问“为什么要替换？”“替换的依据是什么？”“替换前后数量关系有何变化？”等问题，帮助学生理解等价替换的意义。

（四）数形结合策略

数形结合思想是根据数和形之间的对应关系，通过数和形的相互转化解决问题的思想方法。小学中的数形结合思想是把数学问题中的数量关系与空间形式结合起来进行思考，借助图形分析理解概念与数量关系，借助数的规律与计算量化形的特征，以数辅形，让数和形各展所长，使数学知识与问题化难为易，化繁为简，实现思维逻辑与形象思维的统一。

在一年级上册解决问题的建模过程中，教材呈现了很多“数与形”结合的方式。在解决问题中主要“以形助数”的方式解决第二步骤“分析与解答”，它的教学思路与策略为不同层次的学生提供分析问题的方法。

1.巧用点子图

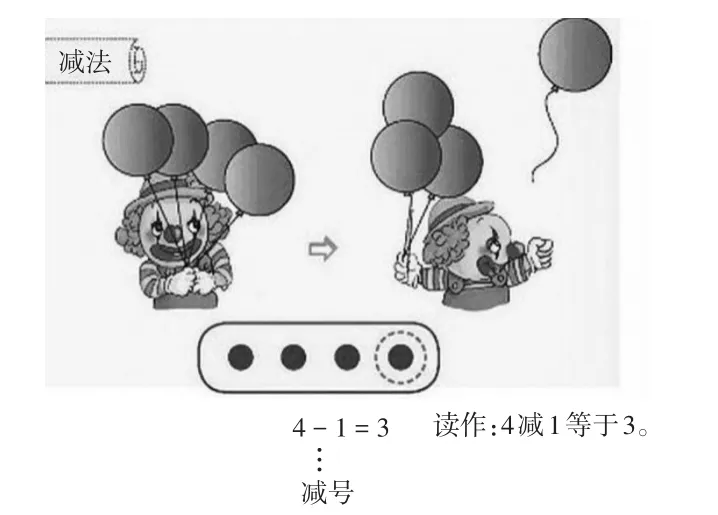
一年级上册P24、P25“加法”和P26、P27“减法”，注重引导学生在情境中理解加法和减法的含义，情境图里增加了表示“合并”或“去掉”含义的点子图，并将数与形、式与图联系起来。学生对减法含义的理解难于对加法含义的理解，但有了点子图的帮助，就会容易得多。如“减法”的含义：从4个气球中飞走（去掉）1个气球，求还剩几个气球，用减法计算。借助点子图理解：从4个点子中去掉1个点子，求剩下几个点子用减法计算。这样，学生的认知就能由直观情境向半抽象过渡。

2.借助线段图

在熟悉加法和减法的含义后，教材P46、P47、P57的“解决问题”的呈现形式主要是通过具体画面创设恰当的情境：用大括号“表示总数（或表示把两部分合起来），用问号“？”表示所要求的问题。情境图配以大括号和问号，呈现一个简单求和的数学问题，使学生明白：知道两个相关的信息和一个相关的问题，就构成一个简单的数学问题。如教材P46“求一共有几只？”和P47“求还剩几只？”，就让学生从情境中感知数学模型，形成解决问题的思路。

教师要引导学生仔细观察情境图，帮助学生排除图中不相干的因素，把目光聚焦于左边和右边的兔子的只数，并在讲清大括号和问号的含义后，请学生试着完整地表达数学问题：左边有4只小兔子宝宝，右边有2只大兔子，求一共有几只兔子？这样学生就在一个生动形象的情境中经历了建模的感知过程。在这个过程中，学生能够发现数学问题，把要求的问题与图里的条件联系起来，为接下来找出解答这道题的策略和数学问题的建模奠定了基础。

新教材中的“解决问题”重视情境创设，虽然内容喜闻乐见，图文并茂，但这些也会成为学生解决问题的障碍：有时会因为复杂信息的干扰使学生抓不住问题的主干。因此，在小学低年级的教学中，教师要引导学生学会认真看图，排除干扰因素，弄清楚图的意思，从而准确、快速地理解题意，为寻找解决问题的策略做好铺垫。

以形助数的关键是要抓住数与形的联系，依据数与形的一一对应关系，构建出图形，从而依据图形解决问题。

（五）变式练习教学策略

促进陈述性知识向程序性知识转变的主要策略是变式练习。变式练习教学的目的是，当学生对某个问题达成共识后，在其他有效学习条件不变的情况下，通过概念和规则例证的变化，缩小学生学习的差异。

1.运用“变式题”，培养学生解决问题的灵活性

例如，题目：一个长方形的长为0.8米，宽为0.3米，剪下一个最大的正方形后，剩下的长方形的周长是多少米？

在学生解决问题后，教师可以将“宽0.3米”分别改为0.1米、0.2米、0.4米、0.5米，再让学生去探究，最后将原题改为“一个长方形长为0.8米，剪下一个最大的正方形后，剩下的长方形的周长是多少米？”在这个过程中，教师只是一个“导演”，学生通过探究和概括，体验到一个“演员”“演出”的乐趣，而且还能探究出剩下的长方形的周长就是原来长方形的两条长的和，这对培养学生灵活选用解决问题策略的能力大有裨益。

2.运用“多解题”，培养解决问题的发散性

“多解题”是指可以从不同的角度去思考的一道习题，这类题目往往要求学生克服思维定式。

例如，题目：鸡兔同笼，一共有20个头和54只脚，鸡和兔各有多少只？

学生对鸡兔同笼问题常用直观画图法、列表筛选法、整体调整法、假设法、方程法，教师还可以引导学生运用比例分配法、矩形转换法、兔子添头法、代数消元法，以此来培养学生的发散性思维。

三、意义

雨果说：“每个人身上都有太阳，关键是让它发光。”毫无疑问，每个学生身上都有闪光点，学生的思考必然会有不同的差异。通过思想的碰撞、差异的融合就会产生新的知识、新的视野和新的智慧。此外，通过肯定学生的差异性，能赋予学生信心，培养学生乐学、善学、会学、学会的心理，且发挥学生的主观能动性，进而保证学生整体而有区别地发展。这样，每一个人都可以倾听不同的声音、获得不同的智慧、走出狭隘的自我、走向更加广阔的世界，最终人人都获得成长和发展。