离散时间多智能体系统群集运动的快速收敛
2018-09-04杨怡泽杨洪勇
杨怡泽,杨洪勇,刘 凡
(1.鲁东大学信息与电气工程学院,山东 烟台 264025;2.新南威尔士大学电气工程与信息学院,澳大利亚 悉尼)
0 引言
多智能体系统作为分布式系统的一个主要分支,在无人机编队、机器人控制、分布式传感器网络等多个领域的应用引起了众多研究者的广泛关注,多智能体系统群集运动已经成为分布式系统中非常重要的研究课题。研究人员主要关注多智能体系统的一致性、群集运动、动态编队等协调控制问题,分析多智能体系统在各种环境下实现协同一致的收敛条件。
针对多智能体系统一致性问题的研究很多[1-6],文献[1]研究了具有动态领航者的时延多自主体系统的一致性。文献[2]研究了具有输入时延的多自主体系统的一致性问题。文献[3]和文献[4]分别就基于均匀采样控制的二阶多智能体系统和基于事件的广义线性多智能体系统,讨论了跟随一致性控制问题。文献[5]研究了在脉冲控制策略下具有动态网络拓扑的多智能体系统的二阶一致性问题。文献[6]讨论了有向网络下带有不同时变时延的多智能体系统平均一致性。
前面文献的研究结果主要关注的是多智能体系统的无限时间渐近收敛,而在实际工程应用中,需要系统在有限时间内达到预期目标,也就是要求系统在有限时间内达到稳定。对于多智能体系统的有限时间收敛问题,文献[7]研究了一组相互作用的智能个体的有限时间一致性问题。文献[8]基于图论、矩阵理论、同质化的扩张和LaSalle不变性原则,设计了多自主体的控制协议,并详细分析了leader-following系统的有限时间一致性。文献[9]提出了一种连续时间非线性分布式协同控制协议,研究了异构多自主体系统的有限时间一致性。文献[10]给出有限时间一致性控制协议,并对所提出的网络协议进行了理论分析,证明了当通信拓扑为联合连通情况时,系统在有限时间可以达到一致。文献[11]研究了具有领航者的多自主体系统的快速有限时间一致性跟踪控制问题。文献[12]总结了有限时间控制系统的研究现状,给出了有限时间控制系统的多种判定条件。
实际工程应用中,系统性能会受到外部干扰的影响。考虑外部干扰等不确定因素的存在,要求多智能体系统的运动轨迹最终会稳定在预设的目标范围内。针对具有干扰的离散时间系统的一致性问题的研究,文献[13]利用网络通信协议和性能拉普拉斯矩阵,把连续时间线性多自主体系统的运动控制问题等价地转化为离散线性系统的稳定性问题。文献[14]研究了具有采样时延的离散时间系统,系统中每个智能体的控制输入只采用其邻域内的其他智能体的状态信息,得到了系统能够实现一致跟踪的充要条件。文献[15]研究了存在建模不确定和扰动项的离散时间系统的有限时间控制问题,给出了系统有限时间有界的充分条件。文献[16]研究了在脉冲控制策略下带有随机扰动的时滞多智能体系统的一致性。文献[17]研究了在网络拓扑结构下,对有外界干扰的二阶离散多智能体系统的均方有界一致性问题。
多智能体系统的包容控制问题,实际上就是一类网络化系统的群集运动。近年来,对离散时间多智能体系统群集运动的研究较少,尤其是对具有外部干扰的多领航者带领网络化系统的有限时间包容控制问题研究更少。本文利用现代控制理论和线性矩阵不等式,研究离散时间情况下具有干扰的多智能体系统的群集运动问题。设计了系统状态反馈控制器,分析了系统在双向通信网络结构下能够实现群体跟踪的有限时间收敛条件。最后对系统进行数值仿真,证明整个系统在有限时间内达到稳定。
1 代数图论及相关引理
本文研究动态多自主体系统的群集运动,智能个体之间通过传感器进行相互通信。假设智能个体为一个点,个体之间相互感应作为连线,这样动态多自主体系统组成了一个具有双向通信的网络拓扑图。

定义1:设集合X={x1,x2,…,xn}为实向量空间的子集,X的凸包定义为
注释1:具有多领航者的多自主体系统的群体跟踪,在多个领航者的引导下,动态自主跟随者在外部控制作用下可以收敛到由领航者所围成的几何区域内,该几何区域就是由多个领航者组成的一个凸包。

1)S<0;
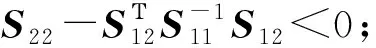
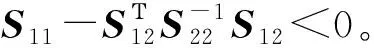
引理2:给定适当维数的矩阵Y,D和E,其中Y是对称的,则
Y+DFE+EΤFΤDΤ<0
对所有满足FΤF≤I的矩阵F成立,当且仅当存在一个常数ε>0使得
Y+εDDΤ+εΤEΤE<0。
2 离散时间多智能体系统包容控制算法分析

考虑如下形式的离散时间多智能体动态方程:
(1)
其中,xi(t)∈Rn是智能体i的位置状态,ui(t)∈Rn是系统的控制输入(即一致性算法/协议),ω(k)∈Rn为系统的外部干扰且满足ωΤ(k)ω(k)
(2)
其中,β>0为控制增益。
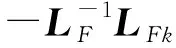
定义2:多智能体系统(1)被称为实现有限时间一致性包容控制,如果存在一个时间T0∈[0,+∞),使得各个智能体的最终状态满足
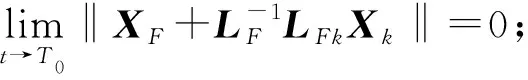
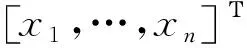
定义3:给定正数δ,ε,d,N,且δ<ε,R为正定矩阵,离散时间系统
x(k+1)=x(k)+u(k)+ω(k)
关于(δ,ε,R,d)是有限时间有界的,如果xΤ(0)Rx(0)≤δ2,都有xΤ(k)Rx(k)≤ε2成立。其中外部干扰ω(k)满足条件ωΤ(k)ω(k) 定理1:应用通信协议(2)的离散时间多智能系统(1)是有限时间有界的,如果存在两个正定矩阵P1,P2,标量γ>1,使得下列两个矩阵不等式成立 (3) (4) 证明:多智能体系统(1)的方程可变化为 (5) 其中控制器为 u(k)=-β(LFXF(k)+LFKXK(k)) (6) (7) 多智能体动态方程可以改写为 (8) 令A=In+(-βLF),得 (9) 假设 (10) 其中γ>1,有式(11)。 (11) (12) 其中 则有 由于 如果 (13) 由Suchur补引理1可得,式(13)等价于式(3),即 (14) 假设(10)成立。根据定义3,可得多智能体系统(1)有限时间有界。 注释2:由于式(14)不是线性矩阵不等式,所以将式(14)左右各乘式(15), (15) 令Q=P-1,得到式(16),即 (16) 矩阵不等式(16)为一个线性矩阵不等式,可以利用Matlab中的LMI工具箱求解计算。 当γ=1时,由定理1可得如下推论: 推论1:系统关于(δ,ε,R,d,N)是有限时间有界的,如果存在两个正定矩阵P1,P2,使得下列两个矩阵不等式成立 (17) (18) 注释3:假设系统中不存在干扰,也就是G=0。则多智能体系统是有限时间收敛的,如果存在一个正定矩阵P1,使得下列两个矩阵不等式成立 (19) (20) 图1 多自主体系统拓扑图Fig.1 The topology of multi-agent system 在连通条件下,考虑2个领航者和3个跟随者组成的连通网络(见图1),图中智能个体4、5为领航者,其余为跟随者。假设拓扑图所有边的权重都是1,系统对应的Laplacian矩阵为 应用Matlab的LMI工具箱计算可得: 图2 离散时间多智能体系统在干扰条件下的运动轨迹Fig.2 The motion trajectory of a discrete multiagent system under disturbance 可见各跟随者在有干扰的情况下,系统的运动轨迹最终渐近收敛到了两个领航者所围成的平面区间[2,3]内,在采样时间k=[4,7]时,跟随者进入两个领导者的平面区间;在采样时间k=[7,12]时,跟随者的运动轨迹逐渐收敛;最终,多领航者运动系统实现了有限时间包容控制。 本文考虑了离散时间多智能动态系统有外部干扰存在下的多领导者带领跟随者在有限时间内达到一致性的问题。本文设置了多领导者的网络系统来重新设计控制协议,结合线性矩阵不等式有限时间收敛理论,给出了离散时间多智能体系统达到领导者有限时间内收敛的充分条件。实验结果显示,本文提出的算法可以快速达到系统稳定,更符合实际工程要求。最后通过数值仿真,验证了本文所提出算法的有效性。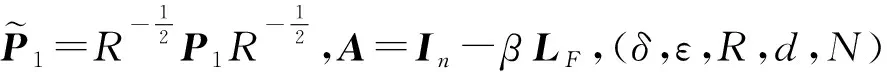
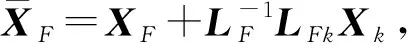

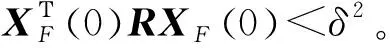

3 仿真验证

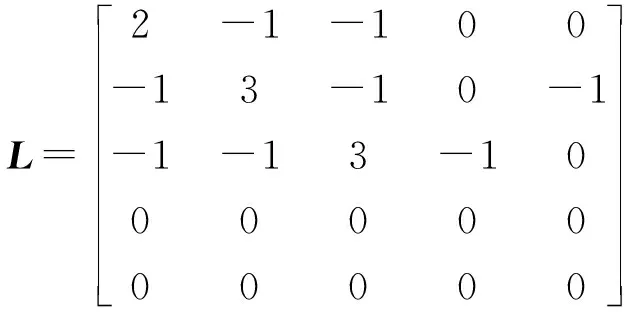


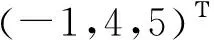
4 结论
