离散Hopfield神经网络的手写数字识别研究

潘园园，张 力，段玲玲，段法兵

(青岛大学复杂性科学研究所，山东 青岛 266071)

0 引言

自1943年McCulloch和Pitts首次提出了人工神经元模型以来，新的神经元模型及其组成的神经网络不断被提出[1-2]，已成为目前非线性科学和计算智能研究的一个主要研究方向。其中，神经网络图像识别技术随着当代计算机技术、图像处理、人工智能、模式识别理论等快速发展，是传统图像识别方法与神经网络算法相融合的一种图像识别方法[3-4]。利用神经网络进行字符识别在计算机识别领域占有越来越重要的地位，并且广泛应用于雾天或者夜晚的交通车牌识别、机器视觉等实际应用领域。近些年来，利用Hopfield神经网络识别噪声字符、汽车牌照字符等实例表明这种方法识别率高、鲁棒性好且具有很好的实用性：例如朱献文[5]研究了基于遗传算法Hopfield神经网络的字符识别方法；魏武[6]等人对车牌字符识别模板匹配的神经网络方法进行改进；丘敏[7]等人在汽车牌照字符识别的应用中将Hopfield和BP网络结合使用提高了识别率；Tatem[8]等人利用了Hopfield神经网络识别遥感图像中的土地覆盖目标。

以上关于字符识别的研究都把噪声作为有害因素，专注于噪声的消除，而忽视了噪声的有益作用，实际上噪声可以增强神经元信息处理能力，即神经科学中的随机共振现象[9-11]。最近，Hopfield神经网络的随机共振现象研究已取得了重大进展，如Katada[9]等人研究了Hopfield网络中随机共振现象，并扩展到包含156个神经元的网络中；Pinamonti[10]等人研究了复杂网络中多峰随机共振的重要特征；Nishimura[11]等人研究了由3个神经元构成的神经网络中随机共振型反馈，将它作为有效的混沌动力学的双势阱模型。

本文主要利用离散Hopfield神经网络识别手写数字，将被识别的图像二进制编码变成串行编码，根据信号在稳态间回环往复的规律输入到Hopfield神经元网络中，不仅研究输入信号幅值调制，码间间隔以及神经元耦合个数对于网络识别图像的影响，还研究了传输过程中噪声强度与图像识别误码率的非线性特性。

1 离散Hopfield神经网络模型与误码率

Hopfield神经网络是由Hopfield[12-13]于1982年首先提出的一种单层的、输出为二值的全连接型的反馈神经网络。离散Hopfield神经网络只有一个神经元层，第0层仅作为网络的输入，并无计算功能，而第1层是神经元层，用于对输入数据和权系数的乘积求累加和，并经非线性激活函数处理后产生输出信息。该网络模拟生物神经网络的记忆机制，具有联想记忆的功能。3个神经元构成的离散Hopfield神经网络可以用加权无向图表示，如图1所示。

图1 离散型Hopfield神经网络结构Fig.1 Architecture of discrete neural networks

从图1可以看出神经元间是相互联系的，并且网络中每一个神经元的输出都反馈到其他神经元上，每条边上权值表示有关神经元之间的连接强度，每个节点代表一个神经元且附有一个阈值，当某神经元所受到的刺激超过其阈值时，神经元就处于激活状态，否则神经元就处于静息状态。我们取神经元激活函数[9]为

(1)

其中,Xi(t+1)表示神经元i的输出(-1≤Xi(t)≤1)，gi表示外部输入信号，ε表示陡度参数，内部电压为

(2)

式中,N表示神经元耦合个数，突触权重ωij是由基本记忆表示为{ξμ|μ=1，2，…，M}的二进制向量集合生成的，Fi(t)为神经元的内部噪声，神经元的组态与网络中储存模式信息的能量值E有关。

(3)

其中,ωii=0表示神经元没有自反馈，令W表示网络N×N的突触权值矩阵，它决定了Hopfield神经网络相应的动力学状态且生成方式为

(4)

(5)

误码率是指二进制码元在数据传输系统中被传错的概率，即传输中的误码和所传输的总码数比值。仿真中将选取的特定图片的像素值输入网络,然后得到相应的信号输出值，网络输出错误信号与图像二进制信号总数的比值得到误码率，误码率越小说明图像传输效果越好，恢复图像就越清晰。

2 仿真和结果

2.1 仿真算法过程

1)读取图像信息：扫描手写的字符图像，得到其灰度矩阵，并进行二值化处理得到BM×N，其中Bij∈{0,1}，其中黑色像素为0，白色为1[14-16]。

2)处理信息：将矩阵改编成一个M×N的二进制字符串，再将其调制成幅值为s，码间间隔为Tb，脉冲持续时间为T的二值幅值脉冲信号S(t)。

3)网络初始化：把t=0时刻的信号S(t)以及噪声初值作为每个神经元的初始值X(0)输入到Hopfield神经网络中，得第1步的输出信号Y(1)。

4)循环更新：将输出按照权重ωij反馈到每一个神经元，同时加入噪声强度为σ的Gauss白噪声，连同下一时刻的信号作为输入，进入Hopfield神经网络，得到输出信号。

5)按照步骤(4)不断更新，得到最终的输出信号Y(t)。

6)计算误码率：将Y(t)进行抽样判决得到解码二进制信号，与初始输入信号比较，计算误码率Pe。

图2 手写数字的图片Fig.2 Picture of handwriteen Character

2.2 仿真结果

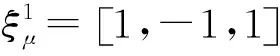
图3～图5就是得到的仿真效果图，可以看出：当网络中没有噪声的时候，网络的输出译码后为空白图像，随着噪声强度的增加，译码图像出现随机共振现象：当噪声强度达到0.25时，译码图像如图3所示，此时选取特定区域的数字渐渐显现；当噪声强度达到0.8时，网络输出数字图像较为清晰，如图4所示；而当噪声强度达到2.8时，噪声强度过大，图像如图5所示，网络输出状态几乎都处于激活的状态(黑色)。

已知生成的神经网络的权系数矩阵是一个对称矩阵，并且对角线元素都为0，由网络的充分条件可知这个网络是稳定的，它可以从任一初态收敛到一个稳态。离散Hopfield神经网络的稳定性可用能量函数即式(3)进行分析，并且满足上述条件的神经网络都有一些共同的特点：在网络信息传输过程中，能量会不断减少。仿真中初始状态确定后使得网络状态向着能量递减的方向转移，最后接近或者达到平衡点，也就组成了仿真最后的稳定性输出状态。图6给出了不同幅值调制信号情况下误码率随着噪声强度变化的曲线，从中可以看出随着调制信号幅值增大，调制信号的能量越大，网络输出图像的误码率也越低。给定信号幅值，误码率随着噪声强度的变化出现非周期随机共振现象，在噪声强度0.6-0.9区域达到最小值4.7×10-3。给定噪声强度下，图7给出了误码率与调制信号码间间隔的变化曲线[17-20]，可以看出增大信号调制长度有利于减小误码率，使得网络输出信息的正确率增加。图7是关于神经元耦合个数对于误码率影响的仿真分析，当Hopfield神经网络神经元耦合个数增加时，网络的误码率产生明显的递减趋势。由式(3)可知神经元网络中每个状态的能量值，在稳定状态时均小于0，其余状态均大于0。随着时间的演化，网络状态总是在能量值最小的稳态之间运动，当网络耦合数增加时，双稳态之间的转换区域增大，神经元输出状态的转换需要更大的码间间隔时间，在传输编码方案不改进的情况下，实验表明增加神经元个数无法进一步减小误码率。

图3 网络在噪声强度为0.25时输出的图像Fig.3 Output Image for the noise intensity of 0.25

图4 网络在噪声强度为0.8时输出的图像Fig.4 Output Image for the noise intensity of 0.8

图5 网络在噪声强度为2.8时输出的图像Fig.5 Output Image for the noise intensity of 2.8

图6 不同幅值信号的误码率Fig.6 Error rate versus different signal amplitudes

图7 不同神经元耦合个数的误码率Fig.7 Error rate versus different neuron coupling numbers

3 结论

本文利用离散Hopfield神经网络模型进行了识别手写数字研究，将手写数字保存为二值图像，由基本记忆形成的神经网络模型对二值图像的像素值矩阵作为输入调制信号进行了处理，通过改变输入信号的幅值大小和信号调制长度，从而对网络输出产生不同影响，从而得到不同识别率下的识别数字图像。研究结果表明，信号调制长度和信号幅值与误码率成负相关，噪声强度对于译码图像识别效果的影响是非线性的，并且合适的噪声强度可以使网络得到清晰的数字图像。进一步地，分别把信号放在不同个数神经元耦合的神经网络里进行传输，研究发现小规模Hopfield神经网络非常适合二进制图像识别问题。本文虽然对不同噪声强度下的离散Hopfield神经网络的随机共振现象进行了证实，但是神经元模型的耦合矩阵是给定的权矩阵，不具有自适应性，因此需要对自适应的耦合系数或随机耦合网络作进一步的动力学分析，对于今后复杂神经系统的研究更具有实际意义。