实现量子异或门的一种新方案

任恒峰,王清亮

(忻州师范学院 物理系,山西 忻州 034000)

0 引言

为了解决计算机中的能耗问题,产生了可逆计算机的概念,在此基础上,物理学家提出了量子计算机理论,并进行了进一步的诸多研究[1-7]。相较于经典计算机,量子计算机最重要的优越性是量子并行计算,利用量子并行处理功能,可以使一些经典计算机中只能进行指数算法的问题,在量子计算机中利用多项式算法就能处理,这说明量子并行算法大大提高了量子计算机的效率,可以完成经典计算机无法完成的工作[8-10]。在经典计算机中,逻辑门是实现基本逻辑运算的单元电路,复杂的逻辑运算可以借助逻辑门的功能来实现。与之相类似,在量子计算机中尤其是量子线路的计算模型中,量子逻辑门是一个基本的量子位元逻辑运算单元,因此研究量子逻辑门理论对于实现更为复杂的量子逻辑计算具有非常重要的基础意义[11-13]。量子异或门是量子基本逻辑门之一,可以操控多输入数位对于输出的逻辑关系,因而从理论上研究量子异或门的实现是实现量子计算机必须要攻克的课题之一[14-15]。在本论文中,我们将结合量子硬币博弈和量子逻辑门领域的相关理论,力求提供一套实现量子异或门的可行理论方案。

1 单硬币量子博弈

首先回顾一下经典博弈的过程[4-7]。A、B两人做一经典的硬币游戏:A将一枚硬币放进一个不可透视的盒子中,此时两人都知道硬币状态(头朝上或尾朝上);密封好后将盒子交给B,此后直到盒子打开之前,两人都不知道硬币的状态。B摇晃盒子后交给A;A接到盒子后也将其晃动;再次交给B,B晃动后将盒子打开。起初可约定,假如人头向上则A获胜,否则B胜出。根据概率理论知识可知,两人都有百分之五十的获胜概率。

在量子博弈中,若B所选用的晃动均为量子操作,而A仍采取经典晃动,那么B就完全可以根据自己的意愿采用量子策略来控制此游戏的胜负。

(1)A起初向盒子中投入的硬币为人头面朝上,即其初态可表示为|1〉;则其密度矩阵可表示为:

(1)

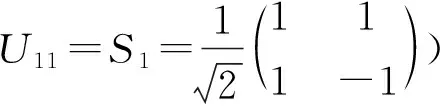
(2)

(3)A的经典晃动将不会改变硬币的密度矩阵,

(3)

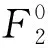
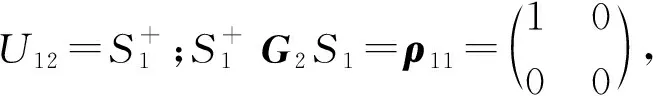
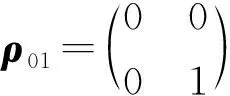
通过以上的过程我们可以得出,B进行首次量子操作后其密度矩阵变成了G2,之后由于A采用的是经典操作，此操作并不会使G2发生改变,那么B就可以采用合适的量子操作来控制游戏的胜负。

2 经典异或门

经典计算机从物理上可以描述为对输入信号序列按一定算法进行变换的机器,其算法由计算机的内部逻辑电路来实现[1-3]。在数字逻辑电路中,可以用1位二进制数码0和1表示一个事物的两种不同逻辑状态。异或是这样一种逻辑关系:当A、B不同时,输出Y为1,而当A、B相同时输出Y为0。只有当每一组输入都不全是1时,输出Y才是1。其真值表如表1所示。

表1 经典异或门真值表

3 量子异或门的实现

3.1 量子异或门的定义

早在20世纪90年代,文献已报道多种实现量子逻辑异或门的方案,比如忽略退相干而考虑冷离子集体量子化行为使离子相互耦合的离子阱方案[9],利用激光对分子的相关控制来实现逻辑异或功能的方案[10]等等。量子异或门的研究一直受到了物理学家的关注,近期,无论是在理论和实验上关于此方面的研究均有了很大程度上的发展,尤其是实验方面,利用激光束控制铍离子实现了并行传输的量子异或门[11],利用纳米尺度的Ge晶体管替代Si晶体管实现了量子异或逻辑功能[12]等等。在这些基础上,我们将提出一种利用量子博弈模型实现量子异或门的可行理论方案。

首先,在定义量子异或门之前,我们做一个规定:

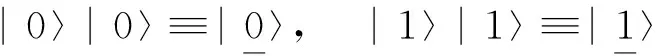
(4)

因而,在经典异或运算的基础上，我们定义的量子异或门就是要实现:

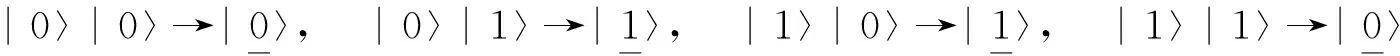
(5)

其中箭头表示量子异或逻辑操作。异或门的每一位信息与单个量子硬币博弈有类似之处,由此可以用两个单硬币量子博弈游戏中的幺正操作来实现量子异或门。

3.2 量子异或门的具体实现

这里,由于量子异或门的输入是两个独立态所组成的信息,因而可以将该逻辑功能与两个单硬币所组成的系统进行类比,利用单硬币量子博弈理论实现量子逻辑功能。在此只需将两个单硬币组合起来即可,其中硬币向上的态来表征|1〉,向下的态来表征|0〉。

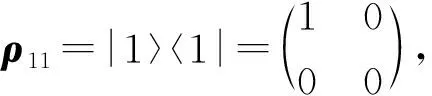
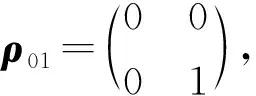
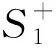
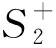
3.3 实现量子异或门的量子系统

由于电子自旋具有的本征态数目与硬币的可能状态数均为两个,我们可以借助两相互独立的电子自旋系统来充当单量子硬币从而实现量子异或门。在实现量子信息传输的诸多方案中,具有经过修正的Heisenberg XX模型的自旋链是一种独具优势的方案,其哈密顿量具体形式为[13],

(6)

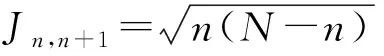
Fig.1 Realization of single-coin quantum game transformation图1 单硬币量子博弈的变换实现

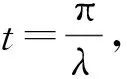
(7)

其中μ0是电子自旋的回转磁比率。当时间t分别取

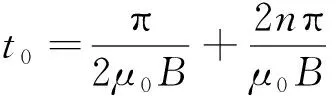
(8)

时,体系的密度矩阵变为ρ2=G2,表明上述磁场作用t1或t0时间后撤去,即是分别对ρ1=|1〉〈1|或ρ1=|0〉〈0|起到了U1的作用。

对于ρ2=G2而言,经典的扰动不会改变最右端格点处电子自旋的状态,为了满足量子异或门的要求,我们需要控制单硬币最终的状态,此时只需给最右端格点处加上一个沿y方向同等大小的磁场,作用t1时间后撤去即可得到ρ1=|1〉〈1|,作用t0时间后撤去即可得到ρ1=|0〉〈0|,这里反方向同大小的磁场分别给最右端格点作用t1或t0时间即是起到了得到两种末态的U2的作用。

4 结论

量子逻辑门是量子计算机的基本元件,量子逻辑功能的实现完全基于量子力学的基本原理。我们基于单量子硬币博弈理论,将经济学中的博弈理论与量子信息中的逻辑门相结合,通过相关的幺正变换实现了量子异或逻辑功能,为量子异或门的实现提供了一套较为可行的理论方案。在我们所采取的方案中,根据量子博弈理论,经典摇动不会改变量子操作的结果,因而表明我们的方案可以很好地避免经典扰动的影响。值得一提的是,本文所提方案可用于解决多个输入信号的量子异或逻辑功能问题。