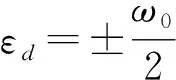温差驱动下正常金属-量子点-超导体系的发热特性

王强,解海卿,薛乃涛

(太原师范学院 物理系,山西 太原 030031)

0 引言

近年来,由于热产生会影响纳米装置工作性能的稳定性和使用寿命,而且还可以提供电流无法探测的电子输运信息,纳米尺度隧穿结中的发热特性受到了实验和理论上的许多关注[1]。多种含电子-声子相互作用的纳米隧穿结用来探索纳米尺度下的发热规律和寻找减小发热量的方法。其中,耦合局域声子库的量子点与正常电极或铁磁电极相连组成的体系因其具有实验上完全可调的系统参数被广泛研究[2-8]。理论研究发现了许多不同于宏观导体的新奇发热现象。比如,零温下发热量存在临界电偏压而电流不存在[2-3],共振隧穿区域为电流很大而发热量很小的理想散热工作区域[3];外加微波场作用下发热量的微分会出现负值[5];外加铁磁电极可以增强电流引起的制冷效应,而且发热量可以通过电极磁化方向来调节[6]。特别是,当电极间存在温度差时,吸收声子的隧穿过程会导致大的电流制冷效应,且存在热电效应很大而发热量小的理想工作区域[7-8]。

最近,在量子点与一端正常电极和一端超导电极组成的隧穿结中,人们发现了新奇的声子辅助的Andreev隧穿和直接隧穿过程[9-10]。当电偏压小于超导能隙时,声子辅助的Andreev隧穿占主导。当电偏压大于超导能隙时,声子辅助的Andreev隧穿和直接隧穿过程同时参与输运。电偏压下相关体系的发热特性也开始受到关注[11-13]。理论研究发现,当量子点与电极弱耦合时,吸收一个声子的Andreev隧穿会引起大的热产生,而吸收一个声子的直接隧穿会使得声子制冷[12];声子辅助的Andreev隧穿引起的发热受超导能隙的影响很大[13]。如果电极间存在温度差,发热除了电流产生的热量外,还可能会有由电声子系统温差引起的热传导能量,发热特性将更加丰富。另外,量子点与正常电极和超导电极耦合体系在温差驱动下的热电效应研究最近取得了重大进展[14-15]。由于超导能隙的存在,量子点耦合超导体系的热电效率会远远高于量子点仅耦合正常电极体系[15]。为了保证量子点耦合超导体系作为热电装置能够稳定工作,也需要研究体系在温差驱动下的发热特性。因此,本文将展开对正常电极-量子点-超导电极隧穿结在温差驱动下发热特性的研究,着重探索在弱耦合情形下不同能级区域的发热规律并揭示热产生的物理机制,找出可能的理想工作区域。

1 理论模型和方法

考虑由单能级量子点与左端正常电极和右端超导电极相连而成的输运系统,整个体系由下面的哈密顿量描述:

H=HN+HS+Hd+HT

(1)

其中:

(2)

(3)

(4)

(5)

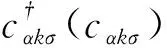
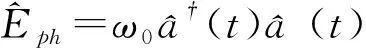
(6)

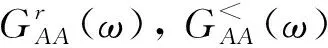
(7)

(8)

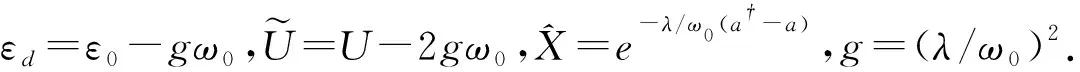
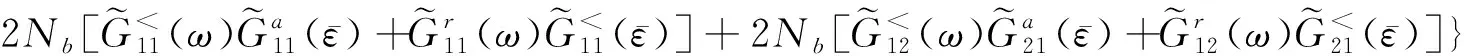
(9)

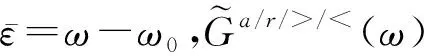
(10)

(11)

2 数值结果与讨论

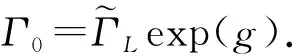
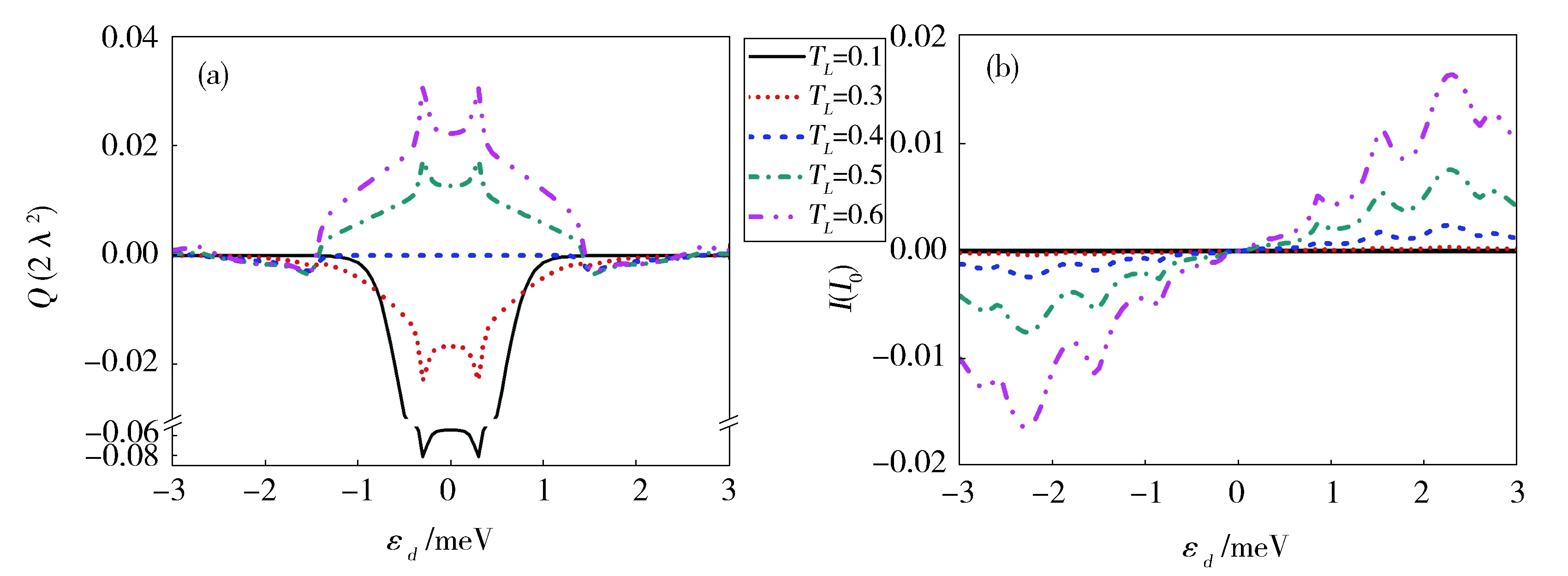
Fig.1 The heat generation Q (a) and current I (b) as a function of the dot’s effectivelevel for different temperature of the left normal lead.The other parameters are chosen as The heat generation and the current are scaled by 2λ2 and I0, respectively.The other parameters are scaled by the energy unit meV其它参数选取为:发热量和电流分别以2λ2和I0为标度,其他参数单位都为能量单位meV图1 (a) 发热量Q和(b)电流I在不同正常电极温度情形下随有效能级的变化情况

Fig.2 The heat generation Q as functions of other system parameters for specific dot’s levelwhen the normal lead is hotter.From left to right panels,the parameter is temperature of the normal lead, the temperature of superconducting lead,the coupling between the quantum dot and superconducting lead, respectively. (a1), (a2), (a3),εd=0.6;(b1), (b2), (b3),εd=0.3;(c1), (c2), (c3),εd=1.55. The unit of each parameter is the same as that in Fig.1从左图到右图,变量分别为正常电极温度、超导电极温度和量子点与超导电极耦合强度。(a1),(a2)和(a3)对应能级εd=0.6;(b1),(b2)和(b3)对应能级εd=0.3;(c1),(c2)和(c3)对应能级εd=1.55。相关参数单位选取与图1相同。图2 正常电极作为热端情形时,特定能级处发热量随相关系统参数的变化情况

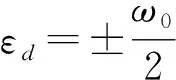
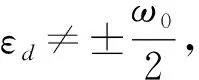
在能级处于超导能隙附近Δ-ω0<|εd|<Δ+ω0的区域,当右端超导电极温度较低时,热传导过程也由正常电极与声子库间温差产生。但是,当左端电极温度超过声子库温度时,发热量仍为负值,如图1(a)所示,这说明此能级区域内流过量子点的电流产生的热量有了很大的贡献。当Δ-ω0<εd(-Δ+ω0>εd)时,左电极上的电子(空穴)可以吸收一个声子直接隧穿到右端超导电极,产生较大的正(负)电流,如图1(b)所示。吸收声子过程引起的电流产生的热量为负值。电流产生的热量和声子库与正常电极间温差产生的热传导能量相互竞争决定着量子点的发热。当左端电极温度TL很低时,被激发到与能级对应化学势处的电子很少,热传导能量和电流产生的热量都很小。如果声子库温度较低,吸收声子的直接隧穿被抑制,热传导过程占主导,发热量随TL升高单调增大并且TL>Tph时发热量为正值,如图2(c1)中实线所示。如果声子库温度比较高,吸收声子的直接隧穿被激发。当TLTph时,热传导能量为正值,但是电流产生的热量开始占主导,导致发热量仍为负值。此时热传导能量会随TL的增大而增大,所以发热量随TL非单调地变化,如图2(c1)中虚线和图1(a)所示。当超导电极温度升高时,大量电子(空穴)被激发到超导能隙上方(下方),粒子的直接隧穿过程被抑制,电流产生的热量减少导致发热量的绝对值相应减小,如图2(c2)所示。从图2(c3)中还可以看出,量子点与正常电极耦合越大,热传导过程越剧烈,而量子点与超导电极耦合越大,电流产生的热量越重要。与冷端耦合越强负发热量的绝对值越大,这一行为与温差驱动下量子点耦合正常电极体系发热特性相同[7-8]。在此能级区域内,电流流过量子点时发热量可以为负值,即热量可以从声子库流向量子点,意味着体系可以作为制冷装置来使用。此外,由图1可知,在εd=±1.4和εd=±2.35附近,电流很大而发热量很小,表明此时温差驱动下的量子点装置可以工作在理想状态。

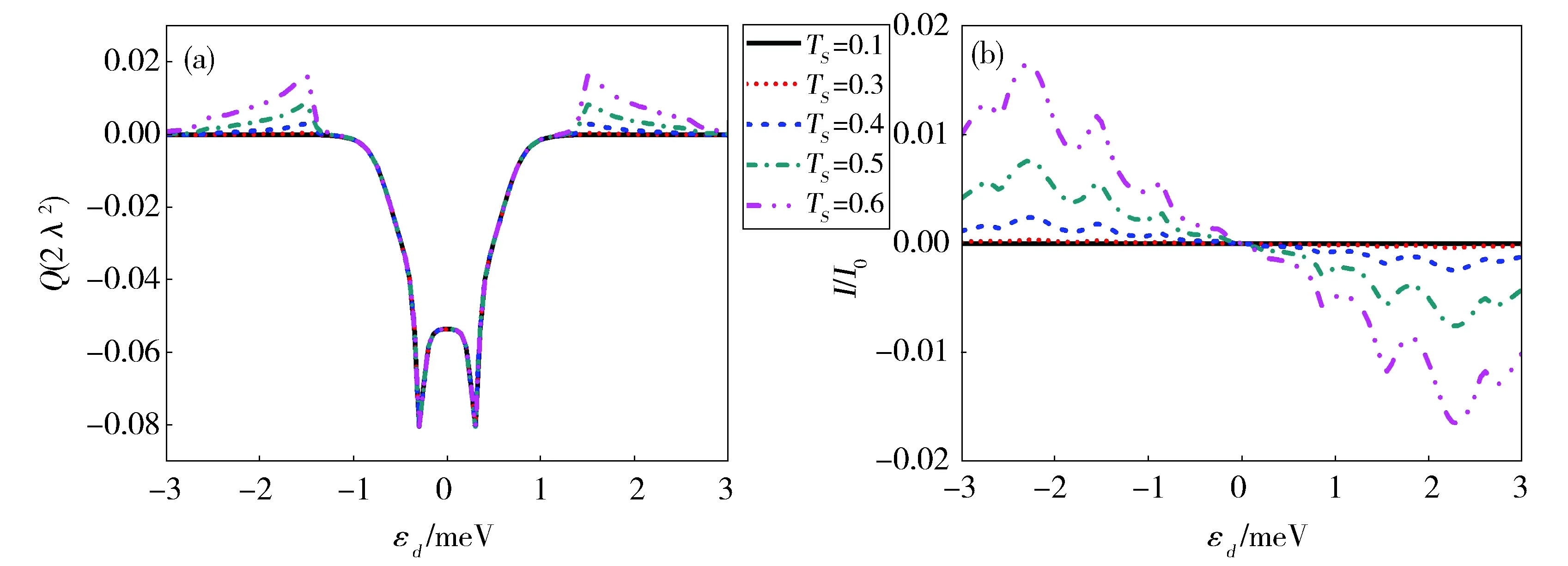
Fig.3 The heat generation Q (a) and current I (b) as a function of thedot’s effective level for different temperature of superconducting lead.The temperatures of the normal lead and phonon bath are chosen as TL=0.1,Tph=0.4,other parameters are the same as those in Fig.1 The unit of each parameter is the same as that in Fig.1电极和声子库温度为TL=0.1,Tph=0.4,其它参数与图1相同。相关参数单位选取与图1相同。图3 (a)发热量Q和(b) 电流I在不同超导电极温度情形下随有效能级的变化关系

接下来,我们考虑右端超导电极作为热电极、左端正常电极作为冷电极的情形。图3给出了给定正常电极和声子库温度时不同超导电极温度下发热量和电流随量子点能级的变化关系。在处于超导能隙深处的能级区域,与正常电极作为热端情形相比,从正常电极隧穿到量子点的粒子由空穴(电子)变为电子(空穴),但是粒子隧穿机制相同,发热还是由正常电极和声子库间温差产生的热传导能量,因此超导电极温度的改变不会影响发热量。在超导能隙附近Δ-ω0<|εd|的区域,发热量随超导电极温度的升高单调地增大。与正常电极作为热端情形相比,此能级区域发热量的绝对值要大很多。这是因为此时超导电极中被激发到超导能隙上方(下方)的电子(空穴)比正常电极多。当能级满足Δ-ω0<εd(εd<-Δ+ω0)时,超导电极上的电子(空穴)可以放出一个声子直接隧穿到左端正常电极,产生了负的(正的)电流,如图3(b)所示。放出声子过程导致电流产生的热量为正,而当超导电极温度较高时由超导电极和声子库温差产生的热传导能量也为正值,二者的贡献叠加导致了大的发热量。不同于正常电极作为热端的情形,此时在超导能隙附近的能级区域量子点发热量由电流产生的热量占主导地位。对于较高的超导电极温度,当声子库温度越高时,尽管热传导能量减小,但是放出声子过程越剧烈,电流产生的热量显著增大,所以发热值越大,如图4(a)所示。当正常电极温度升高时,电流的减小会导致发热量也减少,如图4(b)所示。从图4(c)中还可看出,量子点与超导电极耦合越强,放出声子过程越容易,发热量会越大,而量子点与冷端正常电极耦合越弱,发热量增大的趋势越明显。此外,比较图2(b)和图3(b)所示超导电极作为冷端和热端两种情形下的电流可发现,两电极间温差相同时,相同能级处的电流大小相当,但是由于参与直接隧穿的载流子不同而符号相反。而且,当超导电极作为热端时,在εd=±1.4附近,电流值比较大而发热量很小,也是装置工作的理想区域。

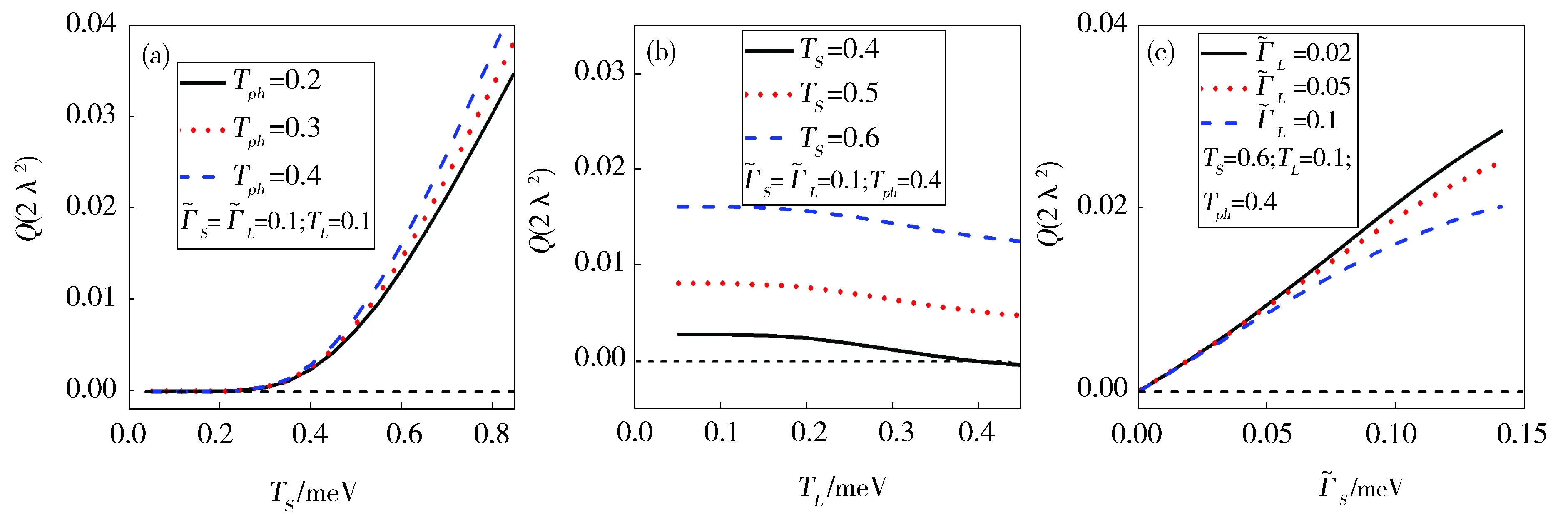
Fig.4 The heat generation as functions of system parameters for εd=1.55 when the superconducting lead is hotter.From left to right panels, the parameter is temperature of superconducting lead, the temperature of the normal lead,the coupling between the quantum dot and superconducting lead, respectively.The unit of each parameter is the same as that in Fig.1从左图到右图,变量分别为超导电极温度、正常电极温度和量子点与超导电极耦合强度。相关参数单位选取与图1相同图4 超导电极作为热端情形下,能级εd=1.55处发热量随相关系统参数的变化情况

3 结论