基于BP网络的产品质量预测-控制模型的研究

张 蕾

(陕西国防工业职业技术学院机械工程学院，陕西 西安 710302)

提高产品质量、降低生产成本是所有企业极力追求的目标，有效控制产品质量是实现这一目标的关键。目前，常见的产品质量控制方法有3种[1]：1)抽样检验法，对随机抽取的产品进行检验，剔除废品，保留合格品；2)统计过程控制法，通过统计、分析产品的质量特征数据来获取产品的质量状态，并对生产过程进行预警；3)智能控制法，建立准确、合理的预测模型并对产品质量进行预测，为优化生产工艺提供参考。

3种方法中，第一、二种方法存在质量控制延后问题；第三种方法虽能提前预测质量参数，却无法实现加工过程的自动调整。为了解决上述问题，本文提出了一种基于BP网络的产品质量预测-控制模型。该模型能提前预测出工件误差，并能根据需要对加工参数进行调整，为优化加工工艺、提高产品质量提供了保障。

1 确定关键参数

机械产品质量的好坏取决于各零件几何参数的加工精度，用误差来衡量。零件几何参数的误差总是随机存在于整个加工过程中，彼此间相互关联、互相渗透，极具复杂性。因此，准确确定影响产品质量的误差因素并对其进行有效控制是提高产品质量的关键。本文结合某制造车间的实际生产过程，将引起加工误差的主要因素[2-7]总结如下：

1)工艺系统刚度K。工艺系统的受力变形会影响零件的加工精度。

2)工件材料硬度HBS。材料硬度不同，加工误差就不同。

3)进给量fi。fi(i=1,2,3)影响工件的变形量，进而影响加工精度。

本文将K，HBS，f1，f2，f3等加工因素作为关键参数，研究产品质量控制方法。

2 基于BP网络的产品质量预测-控制模型

实际生产中，人们不仅希望能提前获知工件的加工误差(质量预测)，还希望在出现超差时系统能自动调节加工参数(质量控制)，以便将工件误差控制在规定的范围之内。考虑到BP网络的非线性映射能力[8-11]，本文将采用BP网络来实现产品质量的预测控制功能，并构建基于BP网络的产品质量预测-控制模型。

2.1 产品质量预测模型

2.1.1网络结构

产品质量预测模型主要用来对生产过程的可靠性进行判断，而可靠性主要取决于误差大小。在构建预测模型时可将加工后的工件误差Eb作为输出，将与工艺过程相关的加工因素K，HBS，f1，f2，f3及加工前误差Ef作为输入，隐含层节点数根据经验选为10。至此，构建出的基于BP网络的产品质量预测模型如图1所示。

2.1.2算法实现

产品质量预测模型中，隐含层和输出层分别采用tagsin函数和purelin函数，具体算法如下：

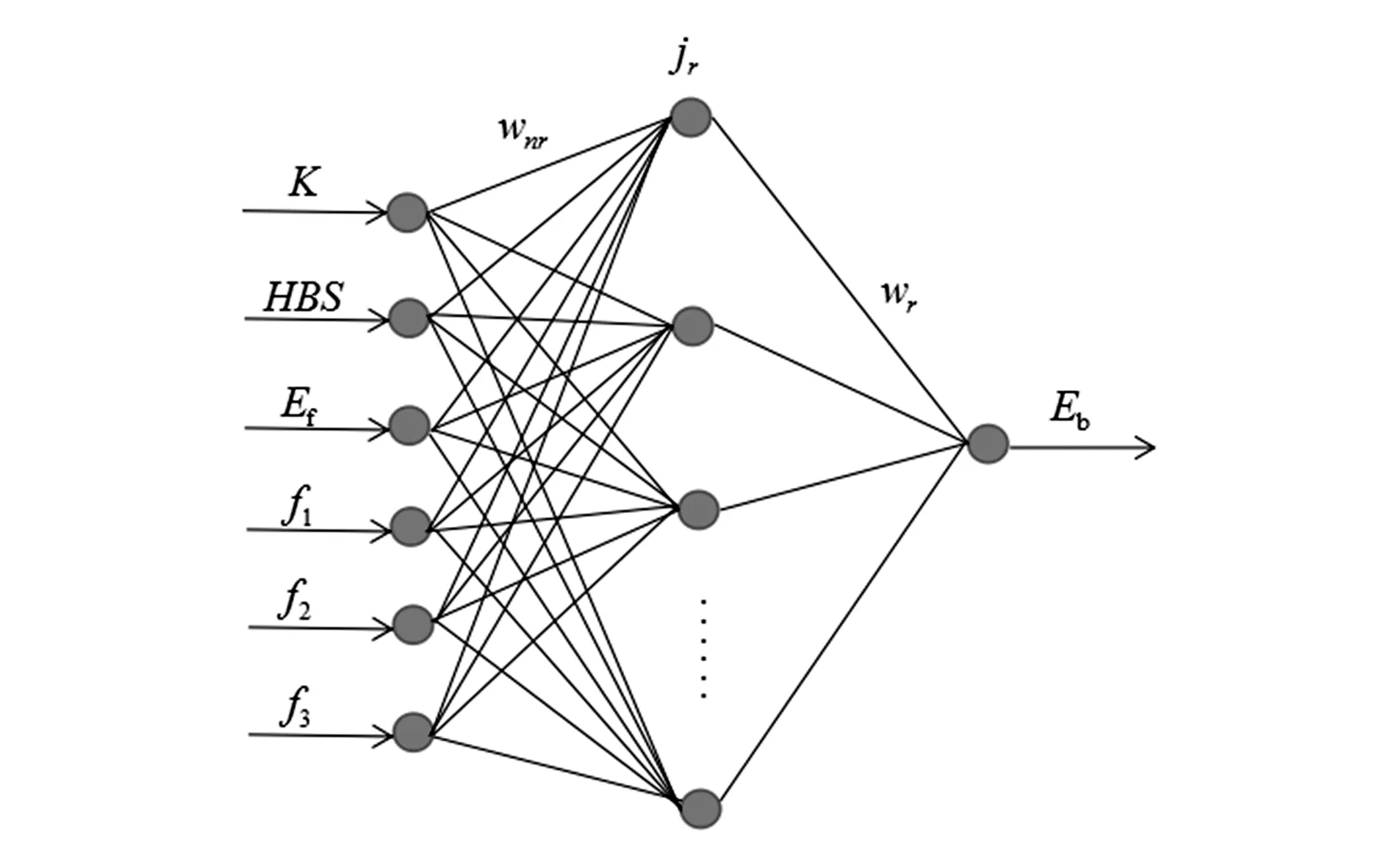
图1 预测模型的网络结构

1)初始化。创建BP网络，将随机非零值赋给连接权值wnr和隐层到输出层的权值wr，n=1,2,…,6；r=1,2,…,10。

2)读入样本数据。给出样本集Xm和工件误差允许值ε。

3)样本归一化。为了避免不同数量级变量间的相互影响，需对样本数据按式(1)进行归一化处理[10]。

(1)

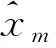
5)判断收敛性。若误差平方和e≤ε，或达到最大迭代次数，学习结束；否则执行误差逆向传播。

6)误差逆向传播。采用批量学习方式，按式(2)修改权值[11]。

w(k+1)=w(k)-[JTJ+μI]-1JTβ

(2)

式中：w(k)和k(k+1)分别为迭代第k次和第(k+1)次时的权值向量；J为雅可比矩阵；β为误差向量；μ为调整因子；I为单位矩阵。

2.1.3网络训练与测试

采用文献[6]中的数据对质量预测模型进行训练，误差曲线如图2所示。

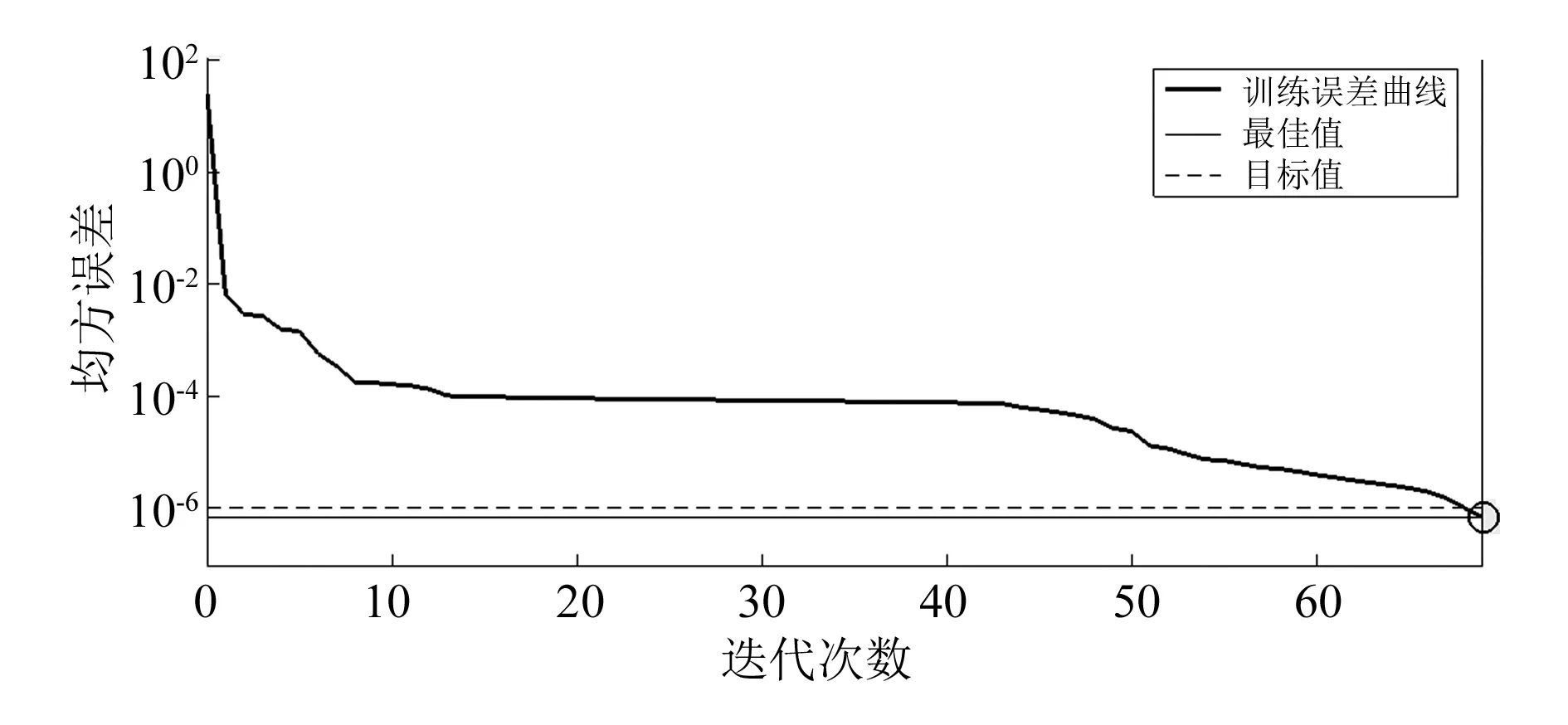
图2 预测模型的误差曲线

由图2可知，经过69次训练后预测模型的输出达到了目标误差1E-6，说明该模型性能稳定，可以用来进行产品质量的预测。

为了验证预测模型的有效性，本文选用某车床的15组加工数据(表1)进行测试。其中，前10组为正常数据，后5组为超差数据，测试结果见表2。表中Eb为误差目标值，Eyb为误差预测值，δ为误差率。

表1 测试样本

表2 预测结果

由测试结果可知，前10组数据的最大误差率为5.3%，后5组数据的最小误差率为9.9%。可见，基于BP网络的产品质量预测模型能较准确地预测出工件的尺寸误差。

2.2 产品质量控制模型

预测模型只能预测出工件的误差大小，无法改变超差结果。要想减小误差，就要借助控制模型对加工参数进行有效调整。

2.2.1网络结构

考虑到加工参数的可控性，本文拟采用调节进给量的方法来对产品质量进行控制，从而可构建出以f1，f2，f3为输出，以K，HBS，Ef和Eb为输入，隐含层节点数为10的产品质量控制模型，如图3所示。

图3 控制模型的网络结构

2.2.2算法实现

由于控制模型的网络结构及误差影响因素与预测模型相似，因此对预测模型的学习算法稍作修改(输入输出、样本集等)即可形成控制模型的学习算法。这里就不再一一赘述。

2.2.3网络训练与测试

采用文献[7]中的超差数据对质量控制模型进行训练，误差曲线如图4所示。

由图4可知，经过118次训练后控制模型的输出达到了目标误差1E-6，说明该模型性能稳定，可以用来进行产品质量的控制。

为了进一步验证控制模型的有效性，本文用表1中的后5组数据进行了测试，结果见表3。表中f1，f2，f3为进给量初始值，fk1，fk2，fk3为进给量输出值。

表3 进给量控制结果 mm/r

由表3可知，fk1，fk2，fk3的每组数据较f1，f2，f3都发生了变化。因此，基于BP网络的产品质量控制模型能有效调整刀具进给量，从而为降低超差率、提高产品质量提供了可能。

2.3 基于BP网络的产品质量预测-控制模型

产品质量的预测模型只能预测出工件的尺寸误差大小，控制模型只能给出一定误差条件下的刀具进给量。因此，要真正实现对产品质量的有效控制，就必须将预测模型和控制模型进行集成，形成产品质量预测-控制模型。

产品质量预测-控制策略如图5所示，预测结果满足质量要求时，正常输出；否则，调用控制模型进行质量控制。

图5 产品质量预测-控制策略

根据预测-控制策略，可确定出基于BP网络的产品质量预测-控制流程，如图6所示。

3 应用实例

本文以某车床加工不同材质的工件为例来验证预测-控制模型的有效性。加工数据见表4，预测-控制结果见表5。

表4 加工数据

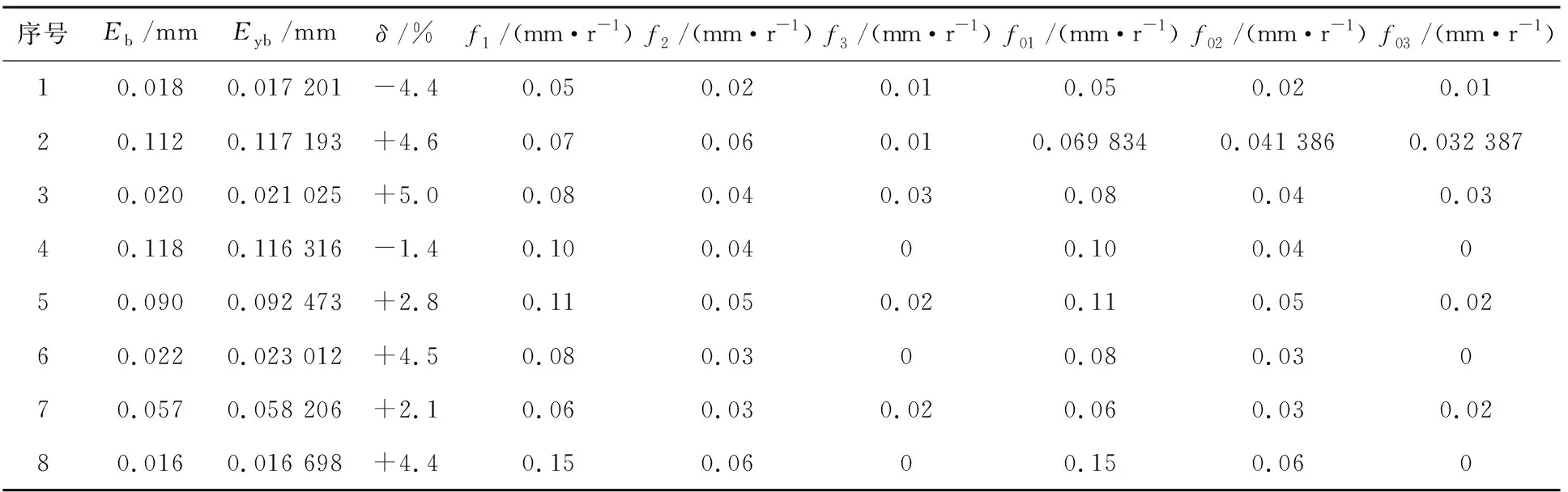
表5 预测-控制结果

图6 预测-控制流程

由表5可知，8组数据的最大误差率均不超过5%，说明其刀具进给量设置都比较合理，加工可靠性较高。

将8组数据中的f1，f2，f3和f01，f02，f03进行对比后发现，第2组f1，f2，f3的数据与f01，f02，f03不符，说明控制前第2组数据是超差数据，预测-控制模型对其进给量进行了调整。最终在新进给量的控制下，第2组数据的Eyb落在了规定的范围之内。可见，基于BP网络的产品质量预测-控制模型能有效降低超差率，为提高产品质量、降低生产成本提供有力保障。

4 结束语

本文构建了一种基于BP网络的产品质量预测-控制模型。该模型通过预测工件的尺寸误差来实现对加工参数的调整和对加工工艺的优化，并最终达到有效控制产品质量的目的，从而为制造企业优化加工过程、降低生产成本、提升企业竞争力提供了较为可靠的参考依据。