不同的视角 别样的精彩*
2018-08-31山东省滨州市北镇中学初中部邢成云
☉山东省滨州市北镇中学初中部 邢成云
“横看成岭侧成峰,远近高低各不同”.苏轼的《题西林壁》富有哲理地道出了观察视角的不同,观察的结果会迥异.解题亦然,由于解题者知识储备的不同、认知结构的差异,对相同问题的思维视角可能相异,从而出现了解题思路的多向性.本文拟通过3个典型题目,多方联想,广开思路,转换视角,追求从另一角度观察与思考问题,在不同的路径中演绎不一样的精彩,藉此为载体,立足数学的核心素养,发展学生思维,提高学生学力.
例1 现行人教版八下教材《勾股定理》一章复习题17(P39)加进了一道拓广探索题(14题),题目如下:
设直角三角形的两条直角边长及斜边上的高分别为a,b及h.求证
视角一(勾股定理):如图1,由勾股定理知,a2+b2=c2,
将其代入a2+b2=c2得a2+b2,=,
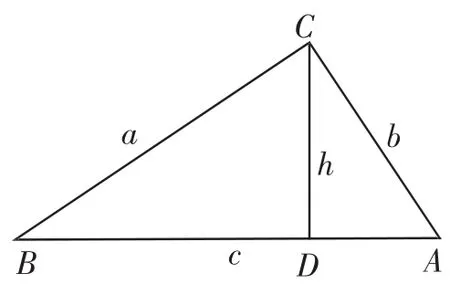
图1
说明:由直角三角形的图形,另由求证的结果中的平方关系,联想到勾股定理应该说是顺乎其理;又由求证结论中出现h,不难想到面积的关系,通过“ab=ch”把勾股定理中的c代换掉(亦即“消除差异”法).以上实践见证了勾股定理与面积关系携手的作用.另外,本题可以衍生出几个问题:
(1)求证:AC2-BC2=AD2-DB2;
(3)求证:以边长分别为a+b,c+h,h的三角形是直角三角形.
视角二(射影定理):设BD=m,则a2=mc,b2=(c-m)c,h2=m(c-m),
即左边=右边,故得证.
说明:笔者通过课程整合,现任的初二学生已经完成了相似性的学习,为了与高中接轨还引入了射影定理,鉴于此,由求证结论的外在结构(出现a2,b2,h2这恰是射影定理的三个“冠头”)联想,射影定理派上用场.从证明过程可见,这个证明从等式的两端分别入手计算,殊途同归,用到的仅是分式的运算,这无疑是自然的思路、大众化的思路,但前提是要学过射影定理.可见,所谓自然思路一定是基于学生的现实的思路,这个现实又与课程标准的基本要求和执教者在教学定位下促成学生的“数学现实”有关.
由于sin2B+cos2B=1,又A+B=90°,则有sin2B+sin2A=1,
两边同时除以h2,得
说明:这一思路同样是较高要求下的产物,三角关系式在新课标中明令不再学习,但笔者带领学生研究三角函数时,很自然地获得这一关系,非刻意求之而得,可见,把这一关系式淡出笔者认为没有必要,实践证明,学生完全可以接受它、学好它.本思路源自“1”的联想以及锐角三角函数的定义式——线段之比.
点评:三个视角,三个思路,各有千秋,且均基于“自然生成”:有结论的平方关系,广泛联想与之相关的数学知识有勾股定理、射影定理、三角函数关系式等,由于注目点的不同、主观意识的差异等,导致了思路的相异.实践证明,在教学中适时抛给学生去思考、去解决,除了巩固现实所学的成果外,更重要的是扩展了学生的思路与视域,使得面对同样的问题,思路不至于逼窄于一隅.广泛的联想产生相异的思路能助推学生想象的积极性,给学生以信心.因此,通透题目的条件展开广泛联想至关重要.
例2 如图2,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
解:(1)证明:略,如图3.
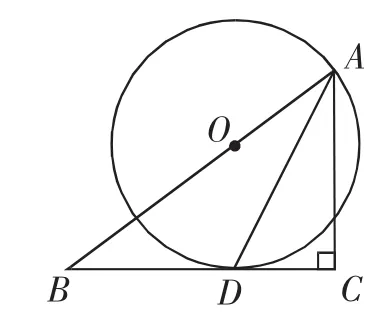
图2
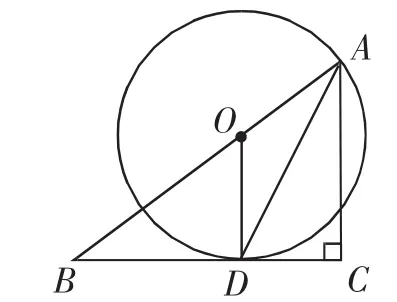
图3
(2)视角1:构造对称.
方法1:如图4,过D作DE⊥AB于E.所以∠AED=∠C=90°.
又因为AD=AD,∠EAD=∠CAD,所以△AED≌△ACD.所以AE=AC,DE=DC=3.
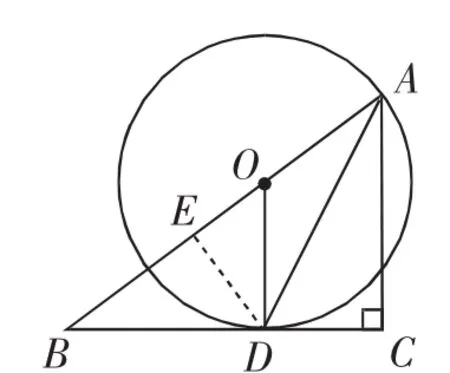
图4
在Rt△BED中,∠BED=90°,由勾股定理,得BE==4.
在Rt△ABC中,(BE+AE)2=AC2+BC2,解得AC=6.
方法2:如图5,延长AC到E,使得AE=AB.
因 为 AD=AD,∠EAD=∠BAD,所以△AED≌△ABD.所以ED=BD=5.
在Rt△DCE中,∠DCE=90°,由勾股定理,得CE=4. 在Rt△ABC中,∠ACB=90°,BC=BD+DC=8.
由勾股定理,得AC2+BC2=AB2,
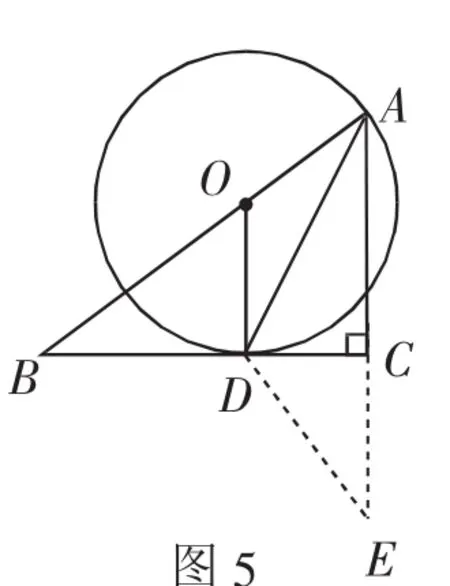
图5
即AC2+82=(AC+4)2.
解得AC=6.
方法3:如图6,记AB与⊙O的交点为E,连接ED并延长交AC的延长线于点F(等价于通过点D作AD的垂线构造对称,其实也是由直径想到直径所对圆周角的构成图的进一步完善).

图6
视角二:构造等腰.
方法4:①如图7,过点C作CE∥AB交AD的延长线于点E,易证△ECD∽△ABD,AC=EC,得,设AC=3k,则AB=5k,由勾股定理得AC2+BC2=AB2,即(3k)2+82=(5k)2,解得k=2,故AC=6.
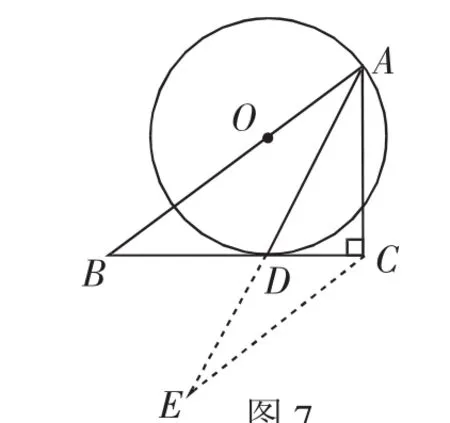
图7

图8
方法5:②如图8,过点B作BE∥AC交AD的延长线于点E,过程基本同于①,略.
方法6:③过点B作BE∥AD交AC于点E,过程略.
方法7:④过点D作DE∥AC交AB于点E(说明:等同于下面的视角三).
视角三:直接利用图中已有的相似模型,如图3.
方法8:由(1)得OD∥AC,易证OD=OA,设OD=x,则AO=x,可有(AB-x)∶x=5∶3,x∶AC=5∶8,则AB=x,AC=x,根据勾股定理得 (x )2= (x )2+82,解得x=,故AC=6.
点评:基于角平分线问题解决的基本视角有二:一是构造等腰三角形视角(源于“角分线+平行线=等腰三角形”,再借助相似);二是对称视角(借力全等的三类构造).另有直接利用图中已有的模型切入,不需要构造其它的辅助线.这是最基本的视角,在一定意义上,这是最经济的思路.可见,视角不同,视点不同,均可生发不同的思路.
(1)构造对称的路径.因为角的平分线就是轴对称图形角的对称轴的一部分,把它复原成对称的形态就会显露内蕴的特性,给解题带来转机或生机,打开思路.而构造的具体方式多样,常见的有三个:由角平分线上的关键点向角的两边作垂线段;过角平分线上关键点作它本身的垂线;根据需求沿对角线翻折等.例2第(2)问题的解答(视角一)作了较好的注解.
(2)构造等腰的路径.由于角平分线的存在,若选择好节点作平行线,可呈现出等腰三角形的模型,同时一条平行线托出了相似基本图,两个模型的联手,外加勾股定理的助力,形成多姿多彩的思路.
所谓第三个视角,无非是一种基于现有图形的直接利用,可归入视角二.
总之,基于角平分线的两个视角都是大众的、常规的、朴实的、自然的,不是高蹈玄妙的杂技.这些返璞归真之法,便于促进学生“基本数学活动经验”的积累,是好的“念头”.
例3 已知两个有公共顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)如图9,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图9,若CB=a,CE=2a,求BM,ME的长;
(3)如图10,当∠BCE=45°时,求证:BM=ME.(只解答第(1)问)
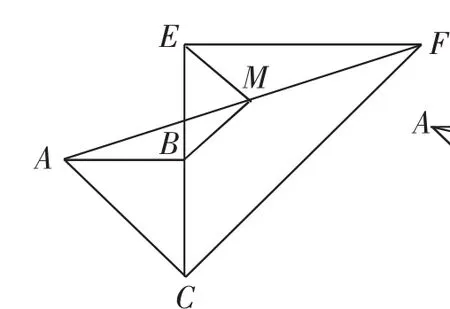
图9
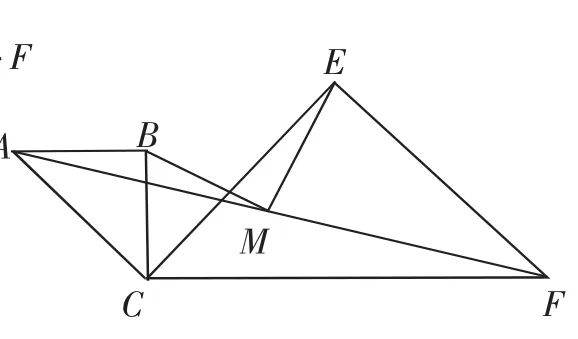
图10
思路一(见中点试旋转):延长BM交EF于D,如图11.
因为∠ABC=∠CEF=90°,所以AB⊥CE,EF⊥CE,所以AB∥EF,所以∠BAM=∠DFM,
因为M是AF的中点,所以AM=MF,
所以△ABM≌△FDM(ASA),所以AB=FD,
因为BE=CE-BC,DE=EF-DF,所以BE=DE,
所以△BDE是等腰直角三角形,
所以∠EBM=45°.
因为在等腰直角△CEF中,∠ECF=45°,所以∠EBM=∠ECF,所以MB∥CF.
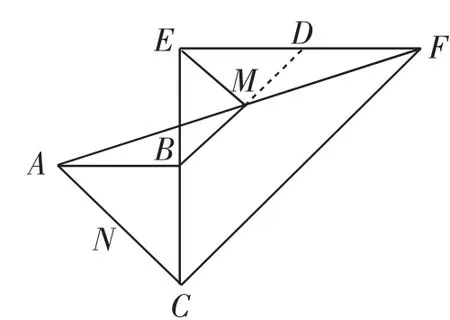
图11

图12
思路二(构造中位线):如图12,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,所以AB=BC=BD,所以点B为线段AD的中点.
又因为点M为线段AF的中点,所以MB为△ADF的中位线,所以MB∥CF.
思路三(斜边中线):连接CM,如图13.
在等腰Rt△ABC和等腰Rt△CEF中,AB=BC,∠ACB=∠ECF=45°,
则∠ACF=90°,所以AM=MC=MF,所以∠MCF=∠MFC,
所以∠AMB=∠CMB.
又∠AMB+∠BMC=∠MCF+∠MFC,所以∠BMC=∠MCF,所以MB∥CF.
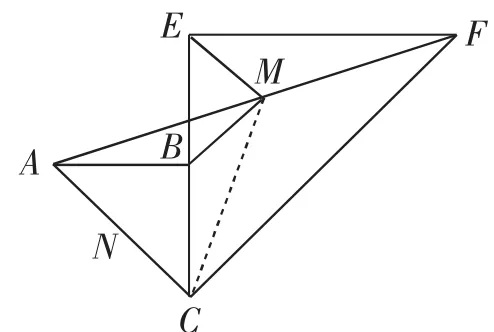
图13
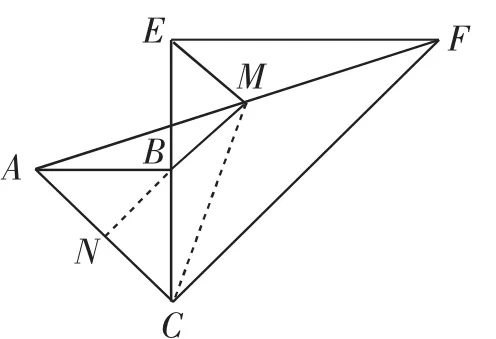
图14
思路四(借助斜边中线,构造中位线):延长MB交AC于N,如图14.
同思路三知,△ABM≌△CBM,所以∠AMB=∠CMB,所以MN⊥AC(三线合一),即∠ANM=90°.
又∠ACF=90°,所以∠ANM=∠ACF,所以MB∥CF
点评:纵然四个思路的视角不同,但都是基于条件中的核心——“M是AF的中点”而展开的联想.作为一个孤零零的中点,其作用是有限的,但让中点变成相关的线,作用就不同了,笔者带领学生总结出了相关中点的基本策略:“有中点试旋转,莫要忘了中位线,直角三角形,斜边中线试试看.”对本题而言,这一基本策略屡试不爽,形成了别样的景观.
一题一世界,一解一菩提.当找不到解题思路,或者只按照常规思路来思考,可能会生发“山重水复疑无路”的困惑,升腾起“独上高楼,望尽天涯路”的茫然;而在“衣带渐宽终不悔”的苦苦追索之下,一旦找对了思路,或换一个视角来思考,就会获得“柳暗花明”“豁然洞开”的愉悦.当此,就有了“蓦然回首,那人却在灯火阑珊处”的惊喜!
写在最后:从不同的角度、不同的方位、不同的层次去审视分析同一题目中的逻辑关联或数量关系,往往会有别样的思路或解法.课堂教学中,努力去营造一个接纳的、支持性的、宽容的课堂氛围,释放学生的智慧潜能,若再适当安排上文的案例活动,给足学生思维的空间,可以激发学生去发现、去创造的强烈欲望,加深学生对所学知识的深刻理解,训练学生对数学思想、数学方法的有效运用,培养学生思维的广阔性和深刻性、灵活性和独创性等思维品质,进而发展学生的学力及创造性思维,使得学生数学核心素养的培养落地.
