从开课情境创设走向“问题驱动”研究——由“直线和圆的位置关系”情境创设说起

☉江苏省泰兴市西城初中 钱 洋

近读《中学数学》（下），王梨洁老师以一节勾股定理应用“青优课”为例对“非数学本质伪情境”的商榷引发笔者感慨和共鸣，一是在当前不少教研活动中的“点赞”式的教研氛围下，能提出作者独立观点，并有理有据的商榷评课，值得敬佩；二是就很多“非数学本质伪情境”来说，确实应该成为“过街之鼠”，影响了高品质数学教学的追求.受到王老师的启发，本文也从一节“青优课”的教学情境说起，对教学情境提出自己的一些实践与思考，提供研讨.

一、“直线和圆的位置关系”的情境创设概述

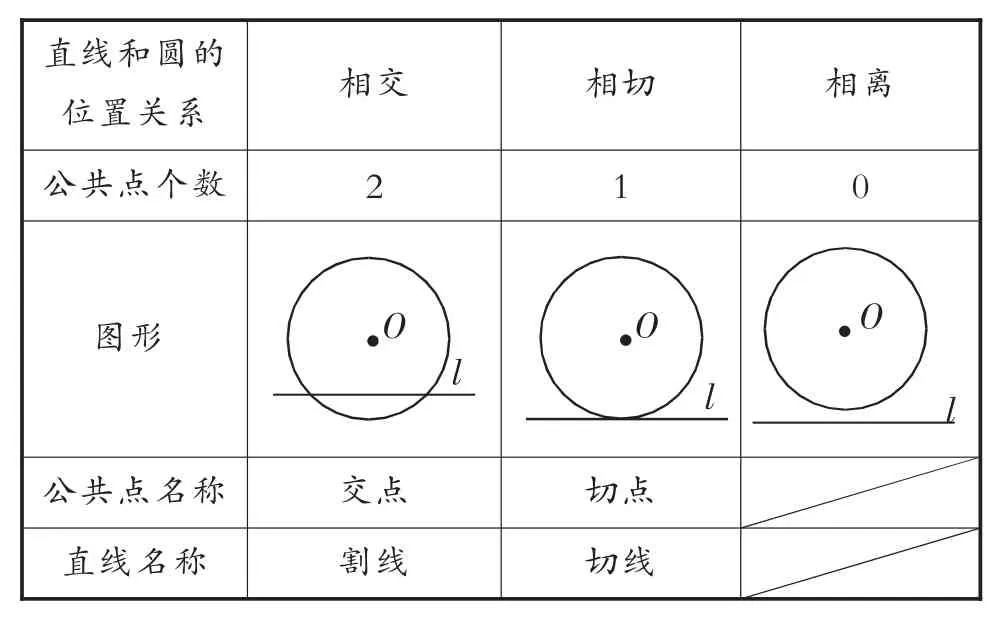
直线和圆的位置关系 相交 相切 相离公共点个数 2 1 0图形 l O O O l公共点名称 交点 切点直线名称 割线 切线l

情景导入：欣赏博鳌美景和《海上日出》视频，如果把太阳看成一个圆，把地平线看成一条直线，太阳升起的过程就体现了直线和圆几种不同的位置关系，直线与圆到底有哪几种位置关系呢？

教学组织：以欣赏视频开课，通过学生观赏亚洲论坛、玉带滩的美景和“海上日出”视频，让学生体会数学来源于生活，增强学生热爱家乡的情感.

构建新知，提出问题：①直线和圆有几种位置关系？

②类比点和圆的位置关系，思考“直线和圆的位置关系可以用哪些量的数量关系来表示”？

③怎样判断直线和圆的位置关系？

教学组织：以设“问”的方式让学生自学，让学生在自学过程中解决问题，从而提高学生的自学能力.在教师问题引导之下学生应该可以回答出直线和圆有相交、相切、相离三种位置关系；进而师生合作归纳出下表：

类比探究：上面从“形”的角度表示了直线和圆的位置关系，那么，还可以用哪些量的数量关系来表示直线和圆的位置关系呢？

引导问题：想想点和圆有几种位置关系？点和圆的位置关系对应了怎样的数量关系？

我们也可用圆心到直线的距离d和圆的半径r的数量关系来表示和对应直线和圆的位置关系，

类比点和圆的位置关系中d与r的数量关系，为探究直线和圆的位置关系中的数量关系做铺垫.

师生活动：请大家在直线和圆的三种位置关系的图形中，画出圆心到直线的距离，然后小组合作探究，当直线和圆相交、相切、相离时，圆心到直线的距离d与半径r有怎样的数量关系？

学生探究后归纳（教师板书）：

直线和圆相交⇔d＜r；直线和圆相切⇔d=r；直线和圆相离⇔d＞r.

接着进入验证、证明、例习题应用与讲评，不是后文关注的重点，限于篇幅，这里略去.

二、关于教学情境创设的一些思考

第一，基于数学知识逻辑连贯的视角优选“开课情境”

以文1批判的“非数学本质的伪情境”来看，本文所选课例中的开课情境（播放视频、欣赏风景）也属于一种非数学本质的生活情境.从章建跃博士前几年一直倡导的基于数学知识的逻辑连贯的视角来看，直线和圆的位置关系是承接点和圆的位置关系而来，开课情境可优选从点和圆的位置关系出发引导学生研究直线和圆的位置关系.更“上位”来看，涉及平面几何所研究图形的三个要素：形状、大小和位置.从七年级几何入门阶段就研究了点和点的位置关系，点和直线的位置关系，直线和直线的位置关系.举例来说，有些学生对尺规作图中的过一点作已知直线的垂线适应性不好，究其根本，是对点与直线有两种位置关系没有辨明，所以当提出过一点作已知直线的垂线时，往往没有先进行分类讨论，想清有两种不同的位置，而两种不同的情形作垂线的作法步骤是有区别的.这样来看，就直线和圆的位置关系来看，也就属于两种图形之间的位置关系，在这基础上还可引导优秀学生继续拓展思考圆和圆的位置关系.

第二，从“数形结合”的观点看直线和圆的位置关系

我们知道，中学数学与小学数学相比有很多不同的学段特点，比如小学更多的是常量数学，而初中开始有变量参与，突出体现在代数、方程、函数这些知识领域；还有，以函数为例，突出体现了“数形结合”的数学思想，这是中学数学最具学段特征的数学思想方法，将原来的方程、方程组、不等式或不等式组都在平面直角坐标系中以函数图像得到高观点的理解.从“数形结合”的观点来深刻理解点和圆和位置关系、直线和圆的位置关系以及圆和圆的位置关系，就能获得一个更高观点的概念理解.因为学生在高中阶段还会继续研究圆的解析式，将圆放置在平面直角坐标系中，从“数”（圆的方程）的角度进行研究.从这个角度来看，虽然是在平面几何的体系下研究圆，但教学时要十分重视“以数驭形”的数学思想的渗透.

第三，从“开课情境”的创设走向“问题驱动”的研究

南京大学哲学系郑毓信教授新近在文4中指出：“问题引领”与“问题驱动”应当被看成“中国数学教学传统”十分重要的一个方面，更为广大一线教师改进教学指明了努力方向.从这个角度来看，很多初任教师把教研精力都过多的放在所谓“开课情境”的设计上，结果像上文课例中一样以一些视频或图文引入新课，看是“有趣”、活跃了课堂的氛围，吸引了学生的眼球和兴趣，但是却弱化了与本课教学内容的联系，有些视频的内容甚至会对学生“静心”于本课所学内容产生干扰作用，比如有些视频中有一些优美、激昂的音乐，有些有一些故事情节夹杂情境之中，学生没有能随着老师的眼光抽象出本课需要学习的数学概念，却还沉浸、陶醉于视频其他内容之中，这就适得其反了.我们的建议是，认真倾听郑毓信教授关于“问题驱动”的教学研究，即精心选取那些能够驱动全课教学进程的问题情境，具体来说，以直线和圆的位置关系为例，返朴归真的问题情境可以这样设计：课前先在黑板上画出三个圆，开课阶段安排学生复习点与直线的位置关系，并让学生到黑板上画出示意图以及点到圆心的距离与点和圆的位置关系之间的对应关系，在此基础上，引导学生思考从点到线，自主探究直线与圆的位置关系，再安排学生类比点和圆的位置关系“数形结合”的进行小结归纳.

值得一提的是，“问题驱动”并不是一个新的理念，恰恰相反，问题驱动、任务驱动在我国数学教育课例实践研究中已有很多比较成熟的做法，这里不妨列举两个典型的研究方向：其一，全国著名特级教师、南通市启秀中学李庾南老师及其团队倡导的“单元教学”，往往也是以一个典型问题驱动新课，实施“先见森林、再见树木”的单元教学；其二，华东师范大学汪晓勤教授及其团队倡导的HPM课例研究，也是基于数学史的考证研究，精选历史上一些数学概念或性质或典型问题的历史源流，恰当改编融入到数学教学之中，成为驱动整节课或某个单元数学知识的有效背景与载体.

三、写在后面

教学情境是一个很大的话题，我们从一个具体的直线和圆的位置关系的“开课情境”说起，阐释了一些个性化认识，既不一定准确，更不一定正确，只是想表明，在情境创设这个大话题面前，我们还有很多值得思考的视角，包括一些知名数学教育学者的观点值得我们借鉴和践行.