充液压电液阻俘能器理论分析与实验

李 征 杨志刚 阚君武 李 升 闫 铂

(1.吉林大学机械科学与工程学院， 长春 130022； 2.吉林建筑大学土木工程学院， 长春 130118; 3.浙江师范大学精密机械研究所， 金华 321004； 4.辽阳庆阳特种化工有限公司， 辽阳 111001)

0 引言

随着科技的发展，含有大量微机电系统、无线传感系统、嵌入式系统、无线通讯等技术的小巧、轻便的可穿戴智能设备及便携式产品得到迅速普及和应用[1]。在这些系统中，系统寿命并不取决于系统内机械零件的磨损程度，而是取决于电源装置的使用寿命，特别是在电源更换困难的机电系统中。尽管微小智能设备本身占用空间较少，但这些系统中的电子元件数量众多、分布复杂，要消耗更多的能源，供能问题面临重大挑战，为这些智能元器件提供能源的传统电源尺寸较大，能量密度较低，使用寿命有限，且不能集成于微小系统中，难以满足便携式电子设备的使用需求。虽然微型高性能电池在使用寿命、能量密度等方面性能不断提高，但是其供电寿命终究有限，限制了目前发展迅速的MEMS产品、无线传感器网络和嵌入式系统的应用[2-7]。如何把环境中的能量转化为电能进而全天候地为各种低功耗的电子元件供电[4,8-10]，如何进一步提高微小智能元件的隔振和减振能力也越来越受到人们的重视，现已成为国内外研究热点和急需解决的关键问题[11-13]。

文献[14-31]研究了液体与压电俘能器间相互耦合对各自的影响，并为自供能压电液压振动控制技术提供了前期基础。

针对压电俘能器的研究现状和自供电振动控制的新需求，笔者提出了基于气体/液体耦合作用的压电振动俘能器[31]，其优势在于：流体具缓冲性，可避免压电振子受刚性冲击、可靠性高；易通过流体背压调节降低系统刚度及基频，可实现低频、宽带振动能量回收；易于实现多压电振子同步工作，发电能力强。此外，该类俘能器在发电的同时具有振动抑制效果。

本文通过了解液体振动和压电驱动领域所取得的研究成果和发展动态，在总结和吸收前人经验的基础上，提出一种新型压电液压阻尼减振器，它利用载流压电材料的共振来衰减流体的脉动，通过压电与流体相互耦合作用来实现振动能量回收，并用理论分析与数值仿真相结合的方法来研究该阻尼减振器的吸振和能量回收特性。

1 充液压电液阻俘能器结构与工作原理

充液压电液阻俘能器的结构原理图如图1所示，其中采用圆形质量块和活塞杆作为放大机构，利用振源驱动液压缸上下振动，把液体的这种振动通过放大机构作用到压电片上，由于流体、弹簧和压电液阻俘能器都具有吸振及缓冲作用，导致液压缸活塞振动与压电片的振动不一致，从而使液体振动通过被隔振物体得到控制；液体将这种变化通过传递到换能器的压电振子致使压电振子产生往复交替变形，压电振子将机械能转换成电能。与传统由单纯的压电振子所构成的振动俘能器不同，利用压电体与流体的相互耦合作用来实现运动的传递与能量转换，能实现多个压电振子协同工作，尤其可用于低频、大振幅振动环境的能量回收。

图1 基于脉动流体减振的压电发电装置原理图 Fig.1 Principle sketch of piezoelectric power generation based on pulsating fluid damping 1.活塞 2.压电陶瓷片 3.橡胶压块 4.弹簧 5.金属基板 6.附加质量

根据板壳理论，图1中压电发电装置的每层压电复合板可以简化为图2所示的模型。

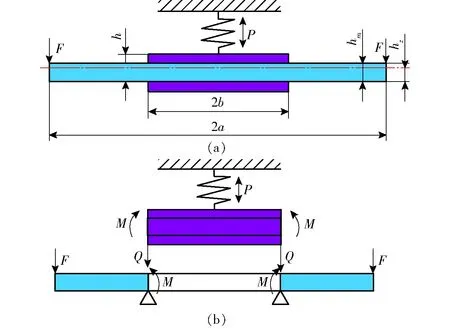
图2 中间支承圆形压电振子的结构及受力图 Fig.2 Structure and stress diagrams of circular piezoelectric vibrator with middle support

图中a——金属基板半径

b——压电陶瓷半径，b=λa

h——圆形压电振子总厚度

对于在内圆半径(r=b)处简支，外边界半径(r=a)为简单边界的整圆板，可将振型表达为两部分：在内圆0≤r≤b区，按中间受集中载荷，周边自由整圆板求解；在外圆环b≤r≤a区，按内圆简支外圆自由的整圆环板求解。

参考文献[32]可知金属基板底部到中性层的距离为

(1)

其中hp=βhhm=(1-β)h

式中hp——压电陶瓷片厚度

hm——金属基板厚度

λ——圆形压电振子的半径比

β——圆形压电振子的厚度比

Em——金属基板弹性模量

Ep——压电陶瓷弹性模量

νm——金属基板泊松比

νp——压电陶瓷泊松比

令

其中ζ=Em/Ep

式中ζ——压电振子的弹性模量比

式(1)可简化为

hz=αh

参考材料学以及压电学相关知识，外力作用下压电陶瓷的内部应力及电场强度分别为

(2)

(3)

(4)

(5)

E3=-g31(T1+T2)+β33TD3

(6)

其中β33T=1/ε33Tε33T=1 300ε0

式中S1——径向应变S2——切向应变

T1——径向应力T2——切向应力

g31——压电常数r——曲率半径

z1、z2——位移w——压电振子挠度

D3——Z方向电位移

E3——Z方向电场强度

β33T——恒应力下介电隔离率

ε33T——恒应力下介电常数

ε0——真空介电常数

图3为压电液阻俘能装置的物理模型简图。

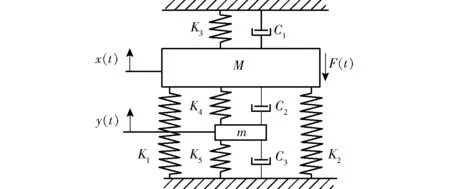
图3 压电液阻俘能装置物理模型 Fig.3 Physical model diagram of a piezoelectric hydraulic energy trapping device

图中M——系统驱动端附加质量和液体质量之和

m——压电振子和振子周边附加质量

K1——承载弹簧刚度

K2——液体等效刚度

C1——液体等效阻尼

C2、C3——串联压电振子等效阻尼，C2=C3

n——鼓型压电振子数量

kp——压电振子等效刚度

F(t)——外部激励

如图3所示，用x1(t)表示质量块的绝对位移，x2(t)表示压电液阻俘能装置中周边质量的绝对位移，F(t)为激振力，则可得运动方程

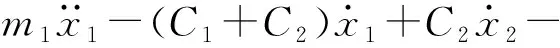
(7)

(8)

式中m1——系统驱动端附加质量和液体质量之和

m2——压电振子和振子周边附加质量

选取外部激振形式为正弦谐波激振形式，即F(t)=Fsin(ωt)，M的稳态响应为

(9)

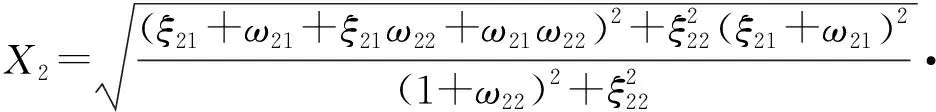
(10)

b=ξ22-ξ11-ξ11ω22-ξ12ξ21-ξ12ω21+ξ22ω11

式中ω——振源的振动角频率位移

压电液阻俘能装置中各个压电振子结构相同，质量块m位移均匀分布于各个压电振子，它们的中心变形量

(11)

根据电荷与电压的关系，得压电振子在外力作用下产生的开路电压

(12)

式中Qg——电荷量Cf——压电振子电容

Dc——内部复合圆板的等效弯曲刚度

令各压电振子的等效刚度为kp、中心点变形量为δ，则有P=kpδ，代入式(12)可得

(13)

单个压电振子发电量

(14)

压电液阻俘能装置的总发电量

(15)

式(15)表明，压电液阻俘能装置的发电性能不仅受圆形压电振子结构、材料特性参数影响，还受到质量块质量、鼓型压电振子组数以及外界激振频率影响。

2 发电性能仿真分析

通过对充液压电液阻俘能器的发电特性进行研究发现，针对外部振动情况要使俘能器的发电性能达到最优，需要对其发电性能进行频响分析，找到各因素对俘能器发电电压频响特性曲线的影响规律，进而在外界振动已知的情况下，通过调整各参数的方法使其发电性能达到最优。下面重点分析激振振幅A、系统背压Pb对俘能器发电电压的影响。

不同激振幅值下电能的频响曲线如图4所示， 图中曲线表明，该俘能器为低频发电装置，当外部激振频率小于20 Hz时，俘能器的发电能力受激振幅值的影响较为明显，通过增大外部激振幅值的方式，可以很明显地提升俘能器的发电能力。外部激振幅值几乎对峰值频率不产生影响。为了确定外部激振幅值是否对峰值频率产生影响，将在后续研究中对其进行讨论。

图4 不同激振幅值下电能的频响曲线 Fig.4 Frequency response curves of electric energy under different exciting amplitudes

对于系统背压Pb分别为0、0.1、0.2、0.3、0.4 MPa时，激振振源频率ω在0～25 Hz之间变化，得到电能的频响曲线如图5所示。

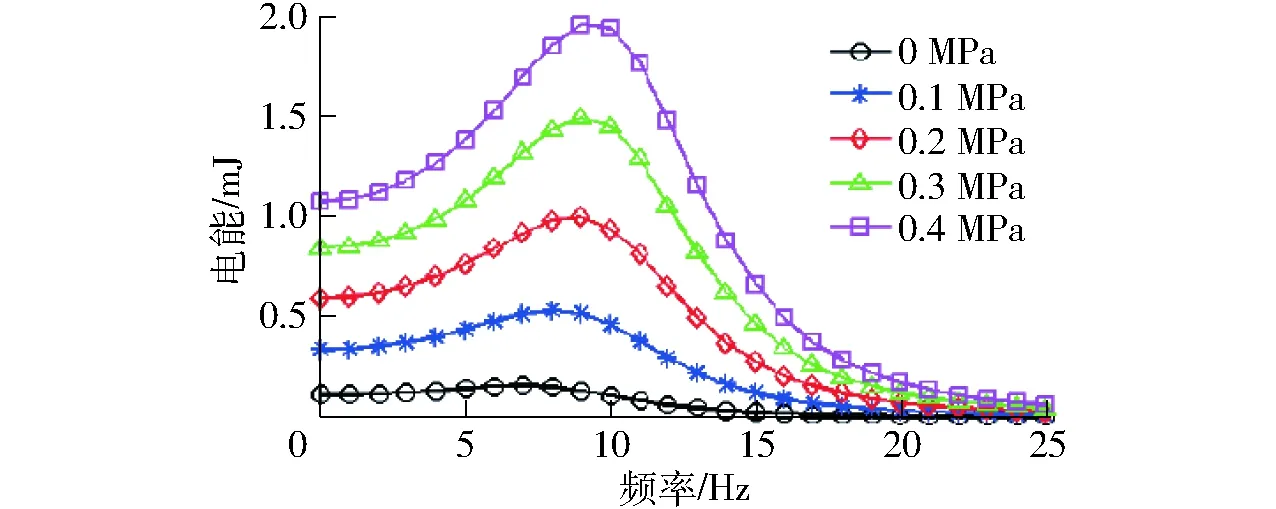
图5 不同系统背压下电能的频响曲线 Fig.5 Frequency response curves of electric energy under different system back pressures

通过对比不同系统背压下电能的频响曲线可知，激振振源的频率在0～20 Hz区间时对俘能器发电能力影响较为明显。并随着系统背压的增加俘能器发电能力也得到提升，其中频响曲线峰值提升较大。图中曲线对比分析后可得到，增大蓄能器中的预置压力可以降低流体的可压缩性，进而减小能量损失，提高俘能器的发电电能。

3 机电等效模型仿真分析

由前面分析可知，机械系统模型可以与电路模型等效，所以充液压电液阻俘能器的机械结构模型可以用电路模型进行等效分析。

系统简化成为具有一个等效质量、一个等效刚度和一个等效阻尼的动力学模型后，整个系统的计算模型和机械线路图如图6所示。如果把机械阻抗取为位移阻抗，图中各要素的位移阻抗为

(16)

式中i——虚部单位

mf——等效质量

Z6和Z7并联为

Z61=Z6+Z7

(17)

Z6、Z7和Z8并联为

Z71=Z8+Z9+Z10

(18)

Z61和Z71串联为

(19)

Z1、Z2、Z3、Z4、Z5、Z62并联为

Z11=Z1+Z2+Z3+Z4+Z5+Z62

(20)

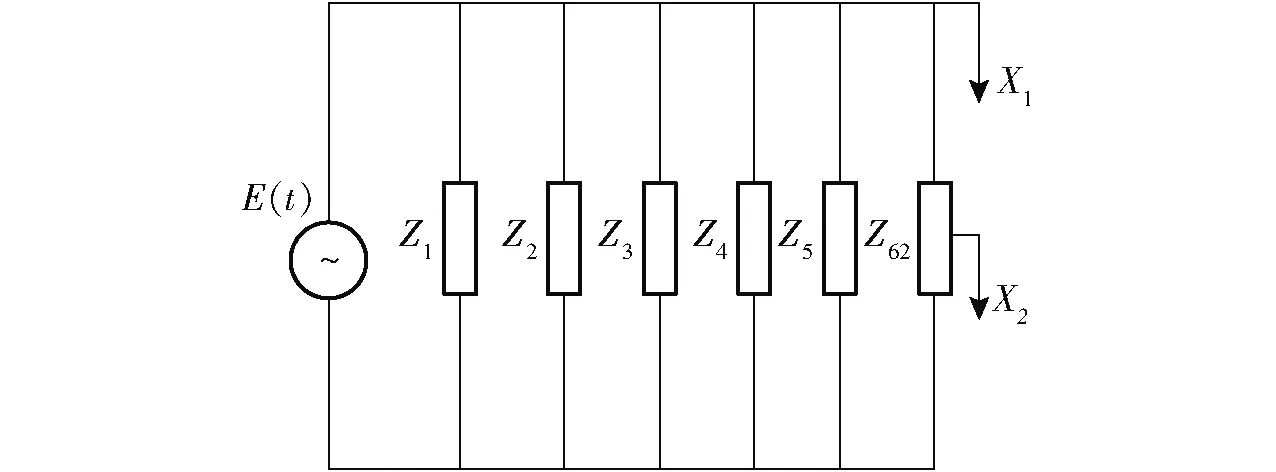
图6 系统模型和系统等效线路图 Fig.6 System model and system equivalent circuit diagram

由图6可知，节点1的位移X1为

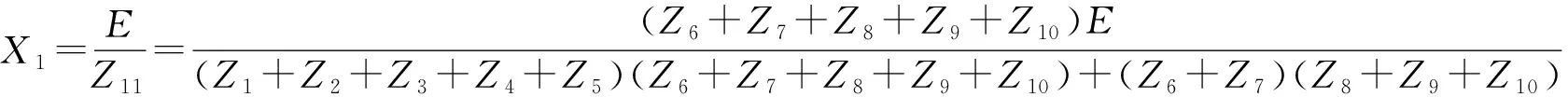
(21)

由公式FZ1=X1Z1得节点1处力

(22)

于是得到传递率Va的表达式为

(23)

具体等效电路图如图7所示。

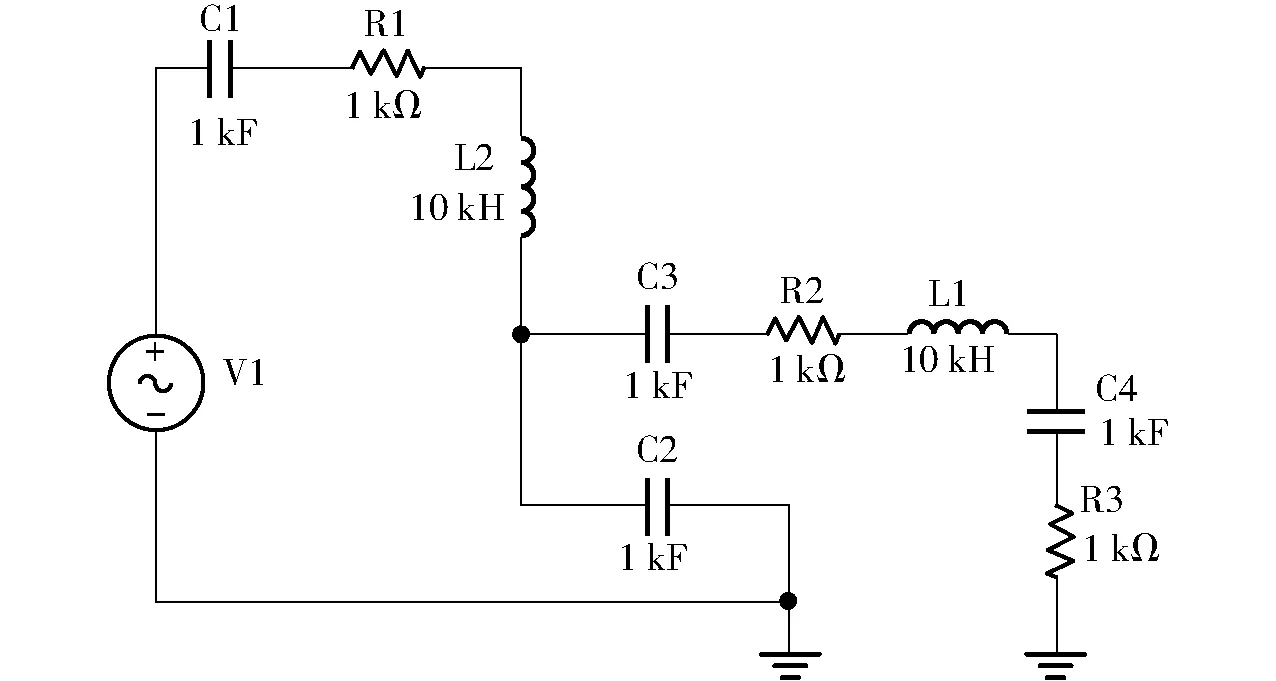
图7 等效电路图 Fig.7 Equivalent circuit diagram

图8 电压-电容特性曲线 Fig.8 Voltage and capacitance characteristic curve

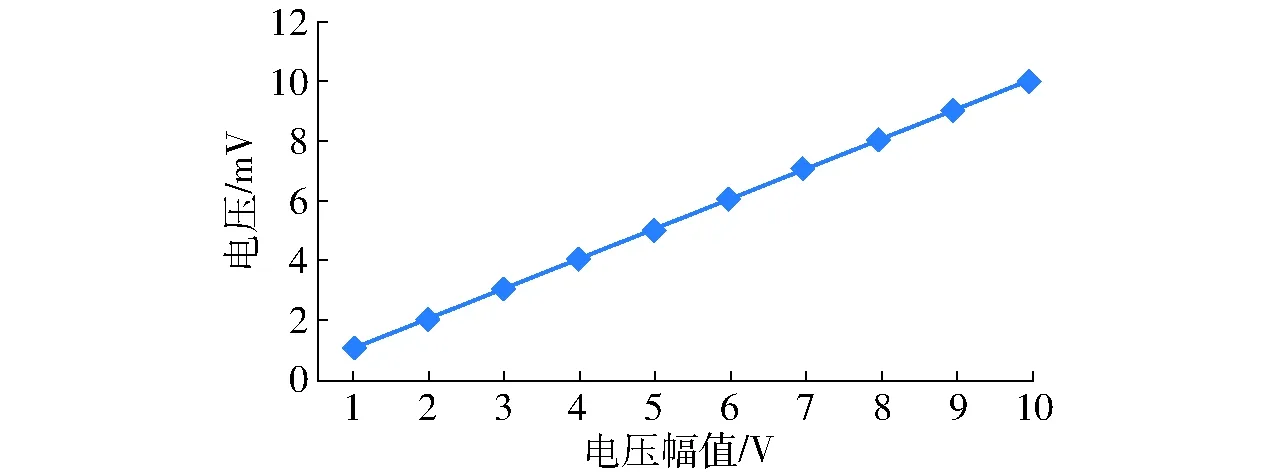
图9 电压-幅值特性曲线 Fig.9 Voltage and amplitude characteristic curve

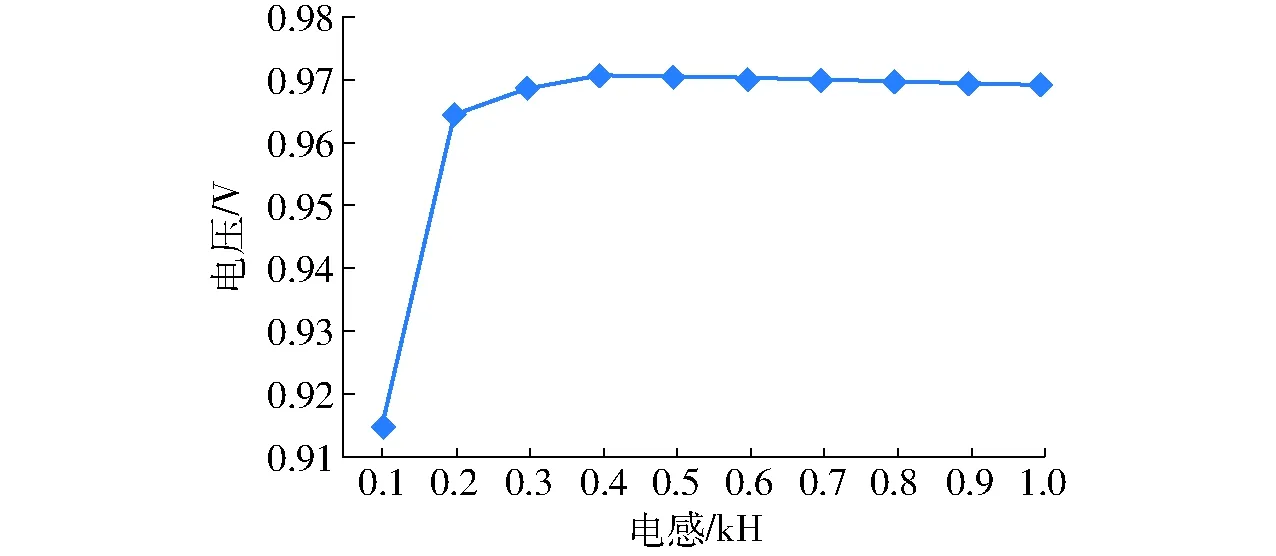
图10 电压-电感特性曲线 Fig.10 Voltage and inductance characteristic curve

由图8不同电容C1下电压曲线可知，电容在1～50 kF区间，电压随电容先增加后减小，有最佳电容使电感(L2)发电电压达到最大，电容为5 kF时，最大发电电压为35.178 mV；图9中曲线表明，在1～10 V区间，电压随着幅值的增加而增加；图10中的电压曲线可知，电感在0～2 kH区间，电压随电感先增大后减小，存在最佳电感使电压达到最大，当电感为0.4 kH时，电压为0.970 55 mV，这与上面仿真分析得到的结论一致，说明设计的电路等效电路图能反映系统机械系统模型图。

4 充液压电液阻俘能器设计与实验

搭建压电液阻俘能器发电实验平台(图11)并进行实验研究。激振器与单头液压缸缸体固定，以水为介质，通过进口1和泄压口对压电液阻俘能器的背压进行调节。通过控制仪控制功率放大器驱动激振台使液压缸振动，并用示波器采集圆形双晶压电振子的电压峰值。

图11 压电液阻俘能器及实验测试平台 Fig.11 Real diagram of piezoelectric liquid trap and experimental platform 1.液压缸 2.压力计 3.蓄能器 4.俘能器 5.示波器 6.功率放大器 7.手动阀 8.激振器

本实验主要对低频运动下的两种情况进行研究分析：第一种是未加质量时如图12所示，激振振源频率在2～15 Hz区间变化时，输出电压变化较为明显，所以在这个区间中任取3个频率作为分析频率。设定系统背压为0.4 MPa，分别在激振振源频率为2.5、3.7、15 Hz下改变激振电压，得到输出电压与激振电压之间的关系曲线如图12所示。

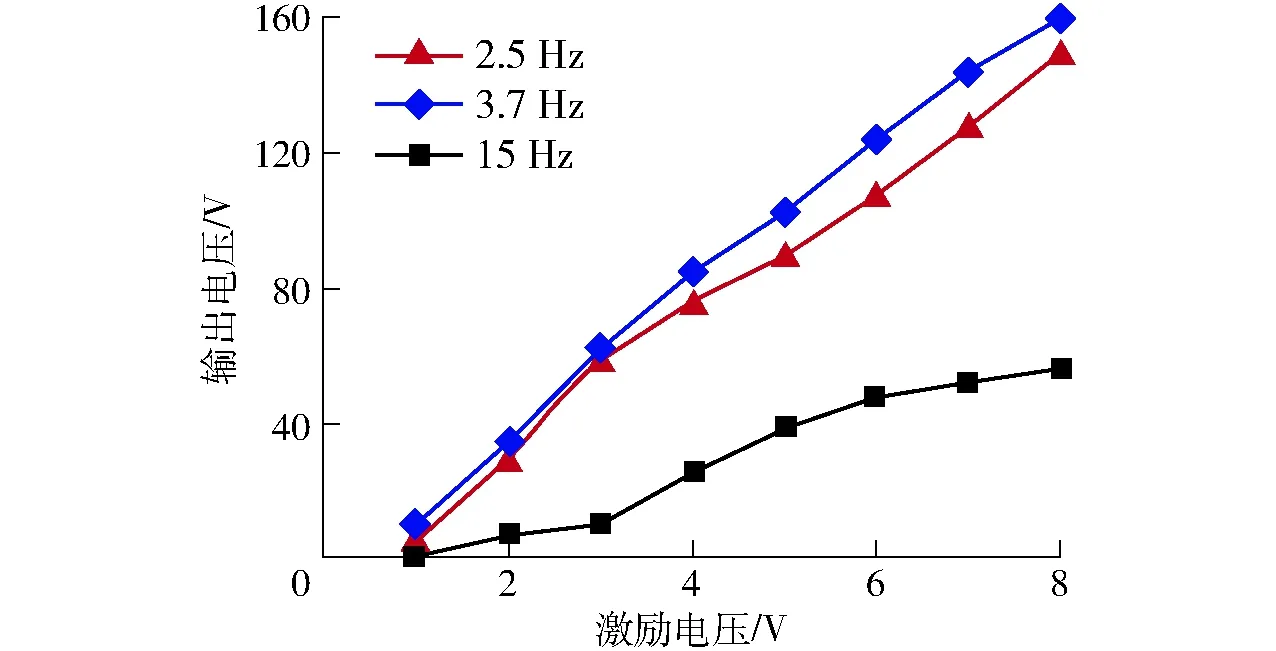
图12 俘能器输出电压与激振器激振电压关系曲线 Fig.12 Relationship curves between output voltage of exciter and exciter excitation voltage

图12中曲线表明，俘能器所受激振电压越大其所对应的输出电压越大，这与仿真分析结果吻合；输出电压与激振电压的关系因激振频率不同而不同。当激振频率为最佳工作频率(3.7 Hz)或靠近最佳工作频率(2.5 Hz)时，输出电压与激振电压之间呈现较好的线性关系；但当激振频率远离最佳工作频率(15 Hz)，输出电压与激振电压之间呈现非线性关系。

另一种情况是加载质量，激振频率在2～15 Hz区间变化时，输出电压变化不明显，而在20～50 Hz区间变化时，输出电压变化较为明显，便于分析，在这个区间中任取了3个频率作为分析频率。质量为10 kg，在实验时采取恒定的激振频率20、40、50 Hz，激振振幅为1 mm，流体介质为水，其他试验条件与前面保持一致不变，以系统背压为自变量，得到的输出电压变化曲线如图13所示。

图13 不同激振频率下输出电压与系统背压的关系曲线 Fig.13 Relationship curves between output voltage and system back pressure at different excitation frequencies

从图13中各曲线的变化趋势可以看出，频率固定的情况下，俘能器的输出电压受系统背压影响很大，随系统背压的增加，发电电压先增加后减小，存在最佳背压使电压达到最大，而且最佳背压还受频率影响；当激振振源频率为20 Hz时，背压为0.7 MPa时产生最大电压100 V；频率为40 Hz，背压为0.6 MPa时产生最大电压为86 V；50 Hz时，背压为0.8 MPa时产生最大电压为81 V。

5 结束语

利用薄板变形的叠加理论建立了集中载荷作用下圆形压电振子位移曲线及发电能力的计算模型。研究结果表明，通过建立机电等效模型，得到结果与理论仿真结果一致，说明所建立的电路模型能够真实反映理论模型的特性。并建立包含了圆形压电振子的尺度及材料性能参数等的模型，可用于该类压电发电装置发电特性的预测、分析及结构优化设计。