并串混联稳定克令吊运动学与动力学建模

李二伟 赵铁石 胡强强 王 唱 耿明超

(1.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004； 2.燕山大学先进锻压成形技术与科学教育部重点实验室, 秦皇岛 066004; 3.河北建筑工程学院机械工程学院， 张家口 075000)

0 引言

近年来随着我国海洋经济的快速发展，海上风电、油气开采及可燃冰开采等海上平台得到了迅猛发展。高海况下，作业船会产生较大的摇荡运动[1]，这些运动会严重影响其上货物向海上平台的安全吊驳。稳定克令吊可以主动补偿作业船的摇荡运动，使吊机末端相对地球稳定，增加海上吊运的作业时间。国外已有具有运动补偿功能的稳定克令吊试验样机和产品[2]投入测试和使用，而国内在海上稳定克令吊这一领域尚未见相关报道。

并联机构[3]具有刚度大、承载能力大、精度高的优点，串联机构具有工作空间大、灵活性高的优点，并串混联机构可以结合两者的优点[4]，因此得到了众多学者的研究。在混联机构构型综合方面，基于不同的理论，很多学者[5-8]综合出了多种混联机构构型。在运动学分析方面，HU[9]提出一个由两个Tricept并联机构串联而成的混联机构，并运用矢量法建立了其完整的解析运动学模型。郭希娟等[10]利用矢量直接求导法建立了一种共轴混联机构的运动学模型。GALLARDO-ALVARADO等[11]把2个3-RPS并联机构串联一起并运用螺旋理论建立了其运动学模型。混联机构的动力学建模方法主要有牛顿-欧拉法[12]、拉格朗日法[13]、凯恩法[14]和虚功原理法[15]。张东胜等[16]基于虚功原理对一个由2R1T并联机构和TR串联机构混联而成的5自由度混联机器人进行了逆动力学分析。MOOSAVIAN等[17]结合牛顿-欧拉法和拉格朗日法建立了一个由平面并联机构和Puma型串联机构混联而成的轮式机器人的解析动力学模型。GUO等[18]提出了一个由3T并联机构和2R串联机构混联而成的5自由度混联机构，并运用具有高效求解速度的基于牛顿-欧拉方程的RNEA方法[19]建立了该混联机构的动力学模型。上述工作推动了混联机构构型分析的发展，为混联机构的工程应用奠定了理论基础。本文提出一种并串混联稳定吊机构，并联部分采用具有虚拟连续转轴的2-DOF RPM[20-21]，其具有静载平衡特性且有较大的载物空间，可以为其上的PRRP串联运动链提供足够的安装空间。

1 并串混联稳定克令吊机构构型分析

1.1 机构选型

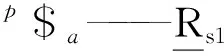
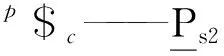
稳定克令吊机构不仅需要补偿作业船的横摇、纵摇和垂荡，且还需实现吊运货物时的变幅、升降和回转。变幅、升降和回转机构采用伸缩式克令吊串联机构Rs1Rs2P，Rs1、Rs2和P分别实现克令吊的回转、变幅和伸缩。作业船横摇、纵摇和垂荡的补偿机构可采用两转一移并联机构或在两转动并联机构的上平台或下平台串联移动单元构成混联机构。

考虑到船上每处的摇摆角度是相同的，但由于“摇”和“荡”的耦合作用，甲板上的垂荡随离转轴的距离不同而有很大差别，而两转一移并联机构三轴之间一般相互耦合，会额外增加驱动单元的行程。因此本文并联部分采用具有虚拟连续转轴的2-DOF RPM，用以补偿船的横摇和纵摇运动。甲板上较大的垂荡运动通过在并联机构的上平台或下平台串联单自由度移动机构来补偿。

如果把单自由度移动机构串联于下平台，则移动机构驱动需承受整个机构及负载的重力和惯性力，这会增加移动机构的驱动功率和制造的复杂性；另一方面，这种布置在补偿状态下只能补偿较小的伴随移动，如图1a所示，上平台仍会产生较大的伴随移动。而把单自由度移动机构串联于上平台，可避免上述问题，另外串联的移动机构可以内嵌到并联机构的载物空间，可以使结构更加紧凑；另一方面，这种布置在补偿状态下，可以补偿较大的伴随移动，如图1b所示。

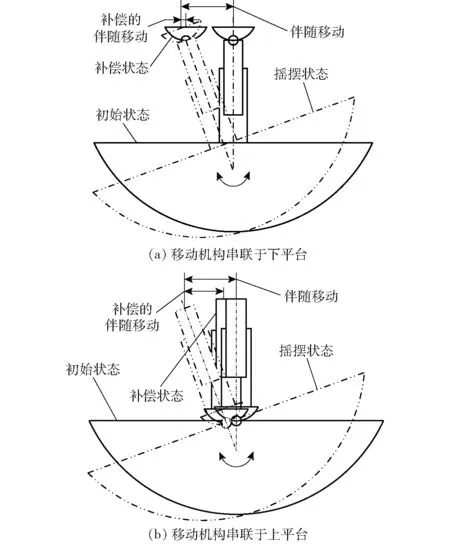
图1 移动机构的布置位置 Fig.1 Arrangement location of prismatic mechanism

1.2 机构描述

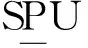
图2 并串混联稳定克令吊机构简图 Fig.2 Schematic diagram of hybrid stabilizing crane 1.下平台 2.上平台 3.中间平台 4.克令吊基座 5.位置可调配重 6.吊点 7.货物

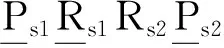
2 位置解

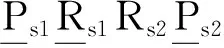
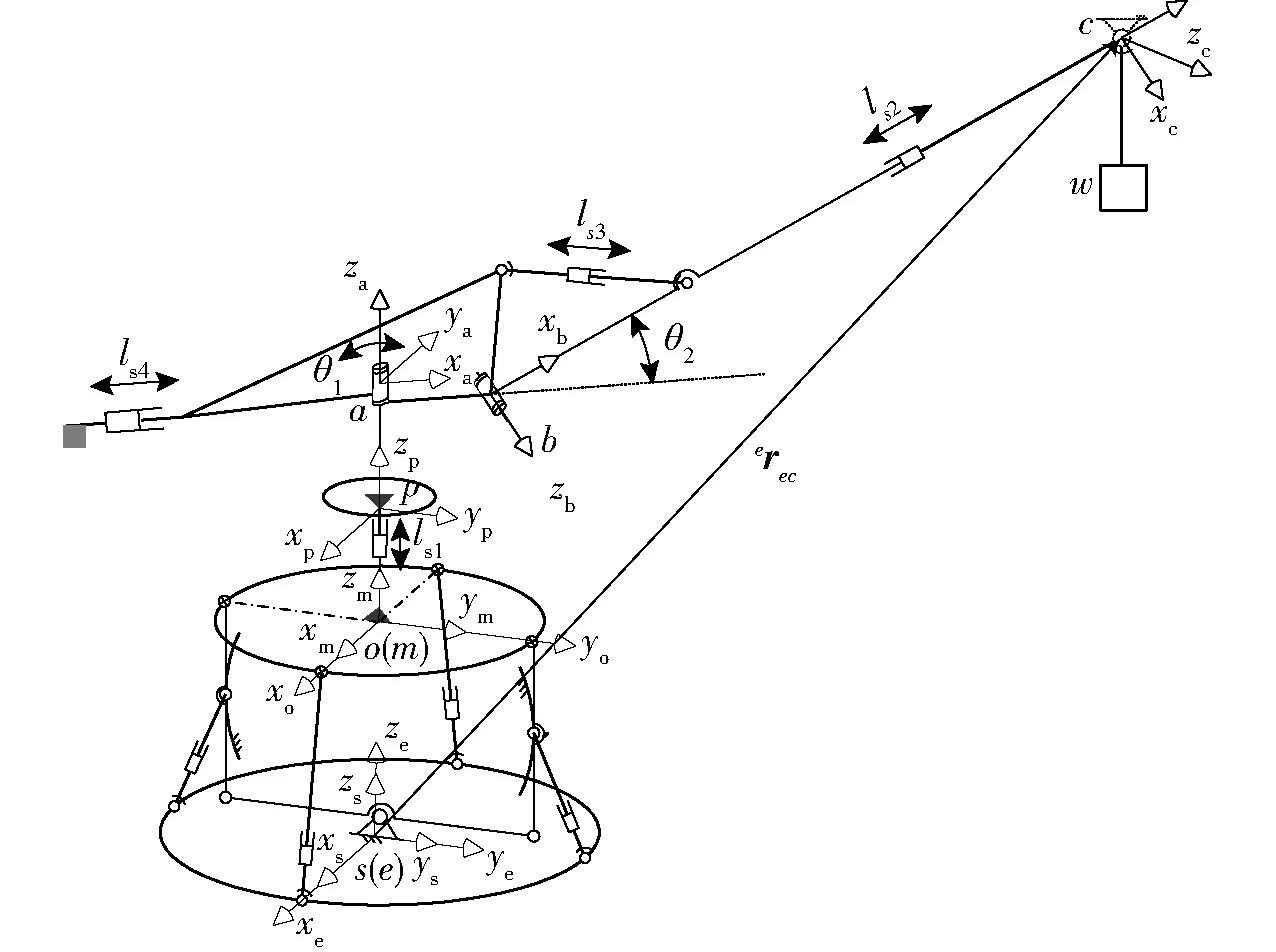
图3 稳定克令吊坐标系 Fig.3 Coordinate system of stabilizing crane

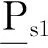
2.1 并联部分的位置解

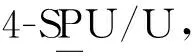
(1)

其中

ori1=ori3+oL(i=1, 3)

式中oli0——初始位置时驱动分支首尾两铰链点的向量

Rom——{m}系相对{o}系的旋转矩阵

Roe——{e}系相对{o}系的旋转矩阵

Res——{s}系相对{e}系的旋转矩阵

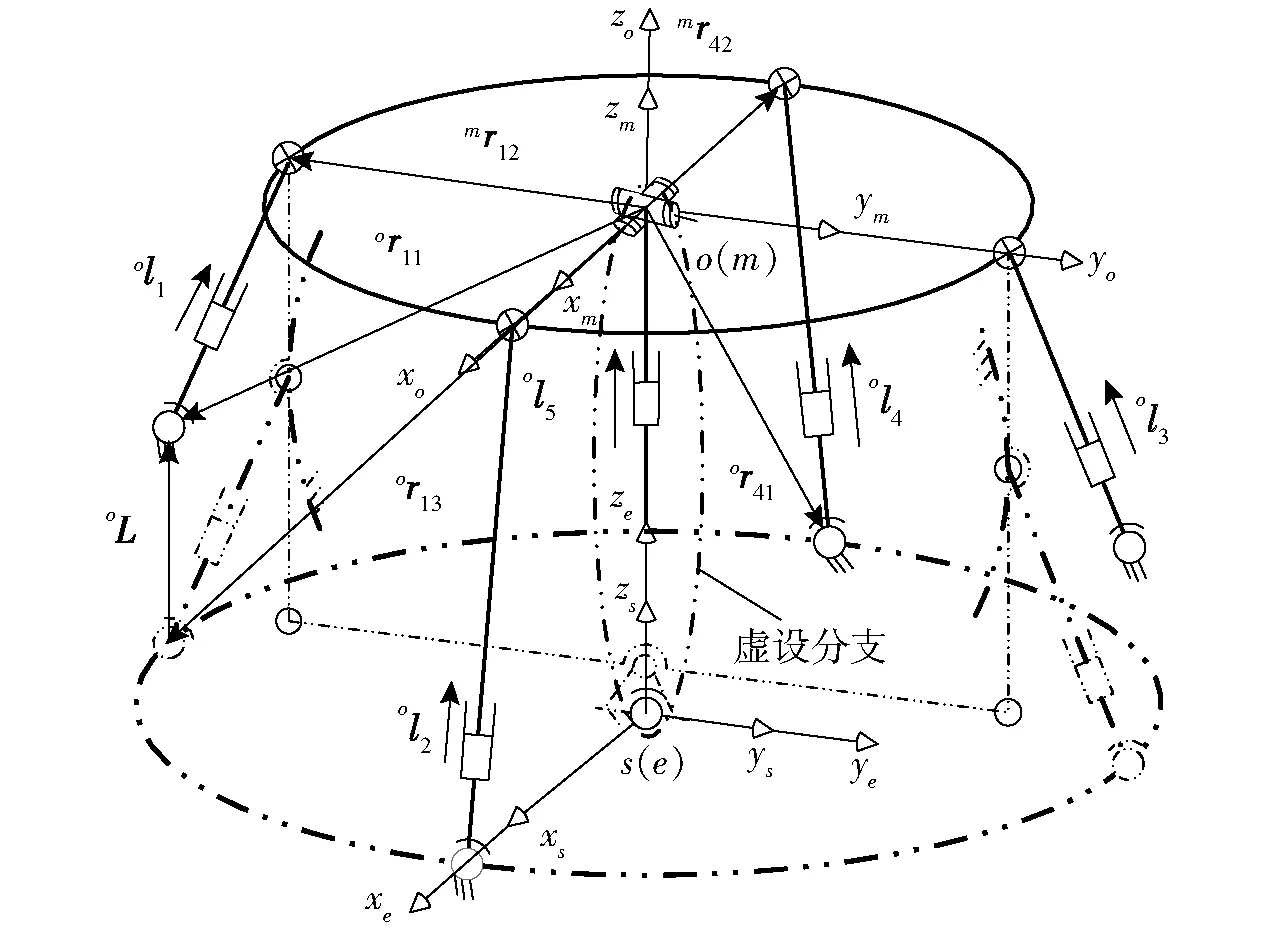
图4 并联部分的等效机构及其虚设机构 Fig.4 Equivalent and virtual mechanism of parallel part

2.2 串联部分的位置解

在补偿模式下，为使稳定克令吊末端吊点相对地球静止(即erec恒定)，则

erep=eres+Reoorso+mrmp

(2)

erec=erep+Rep(prpa+Rpaarab+Rpbbrbc)

(3)

式中Rep——{p}系相对{e}系的旋转矩阵

Rpa——{a}系相对{p}系的旋转矩阵

Rpb——{b}系相对{p}系的旋转矩阵

3 速度与加速度分析

(4)

(5)

由于{o}系与{s}系都与船固结，则eωeo=eωes，eεeo=eεes。结合旋量速度和旋量加速度的物理意义，可得{o}系相对于{e}系的旋量速度eVeo及旋量加速度eAeo分别为

(6)

式中 “^”——矢量的反对称形式或叉乘算子

3.1 并联部分的速度与加速度分析

因为{o}系与{m}系原点一直重合，且补偿模式下，{m}系相对{e}系保持水平，则{m}系相对{o}系表示在{o}系的旋量速度oVom及旋量加速度oAom分别为

(7)

式中O——零矩阵

(8)

式中oex——{o}系x轴的单位向量

oey——{o}系y轴的单位向量

oez——{o}系z轴的单位向量

(9)

3.2 串联部分的速度与加速度分析

根据{m}系、{o}系和{e}系三者之间的旋量速度、旋量加速度关系并结合式(6)、(7)可得{m}系相对{e}系的旋量速度eVem和旋量加速度eAem为

(10)

其中

式中 [* #]——6维旋量*与#的李括号运算

geo——{o}系相对{e}系位姿矩阵

Adgeo——geo的伴随矩阵

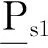
由{p}系、{m}系和{e}系三者之间的旋量速度、旋量加速度关系可求得{p}系相对{m}系表示在{m}系的旋量速度mVmp和旋量加速度mAmp为

(11)

其中

mωmp=O3×1mεmp=O3×1

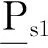
补偿模式下，稳定克令吊末端吊点相对地球系动态静止，相当于稳定克令吊在吊点处通过球铰与地球相连，如图3所示。设{c}系相对{e}系的绝对角速度和绝对角加速度分别为

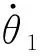
(12)

其中evec=eeceωeceaec=eeceεec

(13)

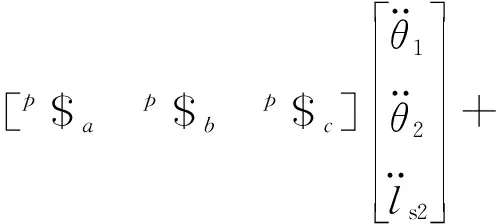
(14)

(15)

式中pVpc——{c}系相对{p}系表示在{p}系的旋量速度

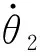
4 动力学分析

mbwmrmac2=-mmmrmmc-mpmrmpc-

mamrmac1-mbmrmbc-mcmrmcc-mwmrmc

(16)

其中

mG#=m#mg

式中mGbw——配重在{m}系的重力矢量

mGm——上平台在{m}系的重力矢量

mGp——中间平台在{m}系的重力矢量

mGa——基座在{m}系的重力矢量

mGb——伸缩臂固定部分在{m}系的重力矢量

mGc——伸缩臂移动部分在{m}系的重力矢量

mGw——货物在{m}系的重力矢量

m#——各相应构件的质量

mg——{m}系的重力加速度矢量

由式(16)可算出稳定克令吊在吊运货物时配重需移动的距离ls4。

图5 稳定吊各主要部件质心 Fig.5 Barycenter of main part of stabilizing crane

4.1 串联部分的动力学分析

(17)

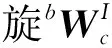
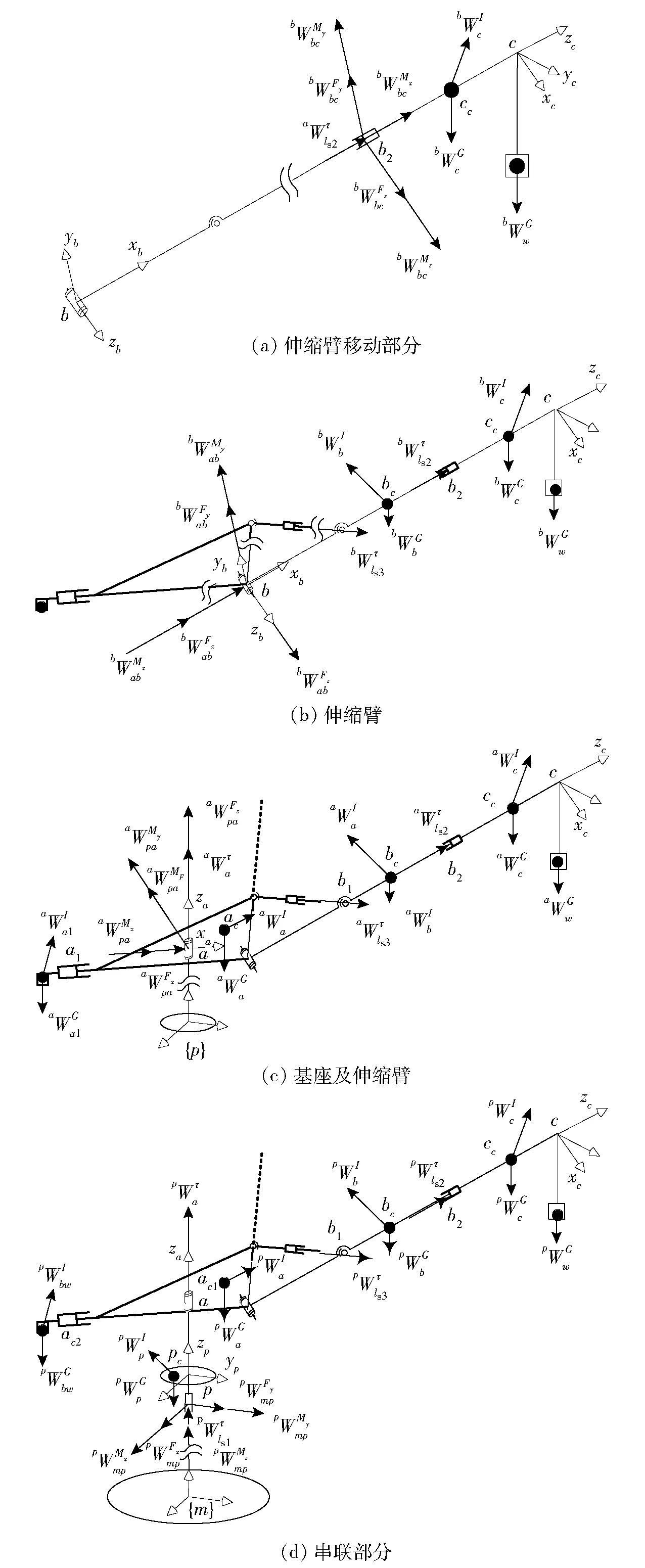
图6 稳定克令吊串联部分受力分析 Fig.6 Force chart of serial part of stabilizing crane

4.2 并联部分的动力学分析

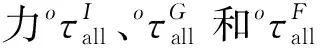
(18)

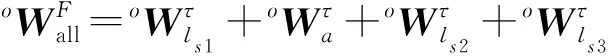
则稳定克令吊并联部分虚设机构的广义驱动力为

(19)

稳定克令吊并联部分第1、第2分支驱动副的驱动力f1、f2分别为oτA的第1、第2个元素。

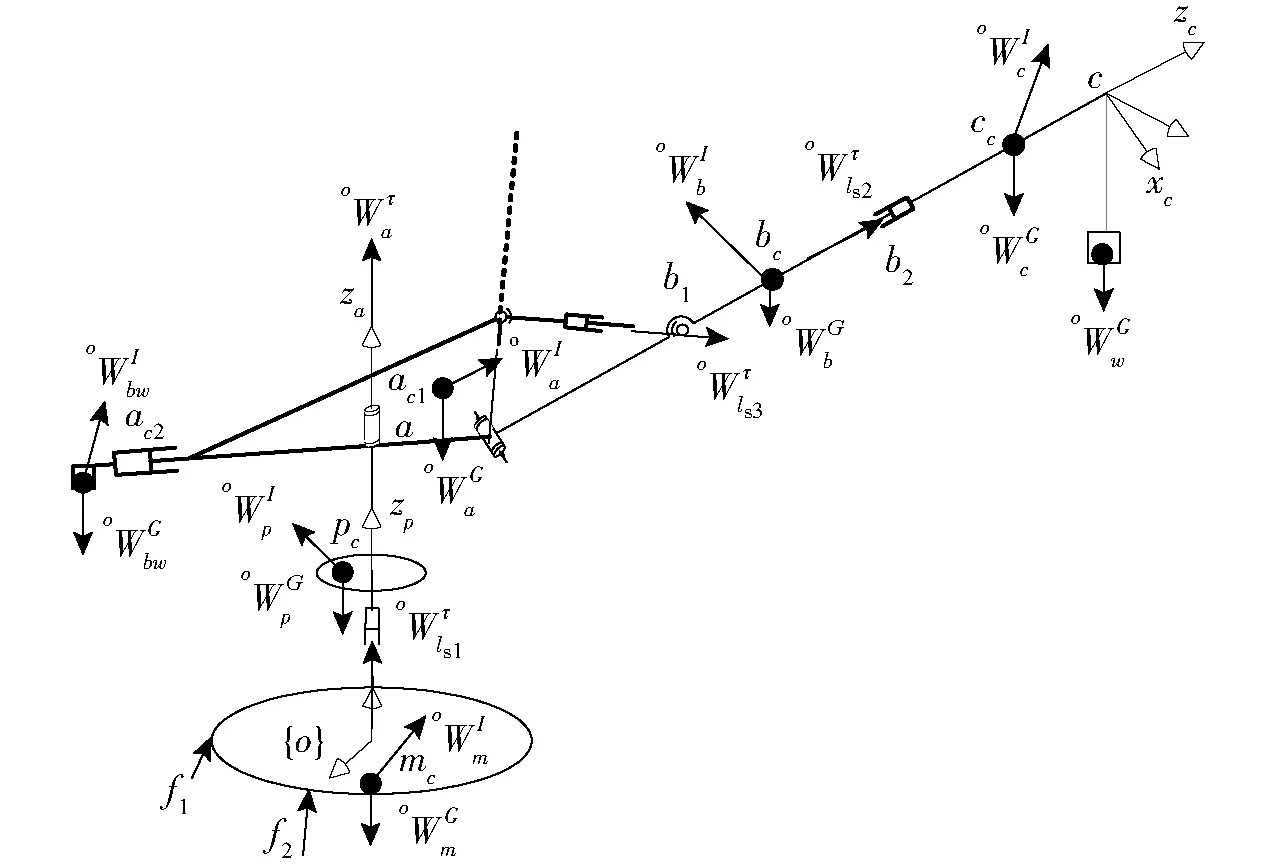
图7 上平台及串联部分整体受力图 Fig.7 Force chart of upper platform and whole serial part of stabilizing crane

5 数值算例

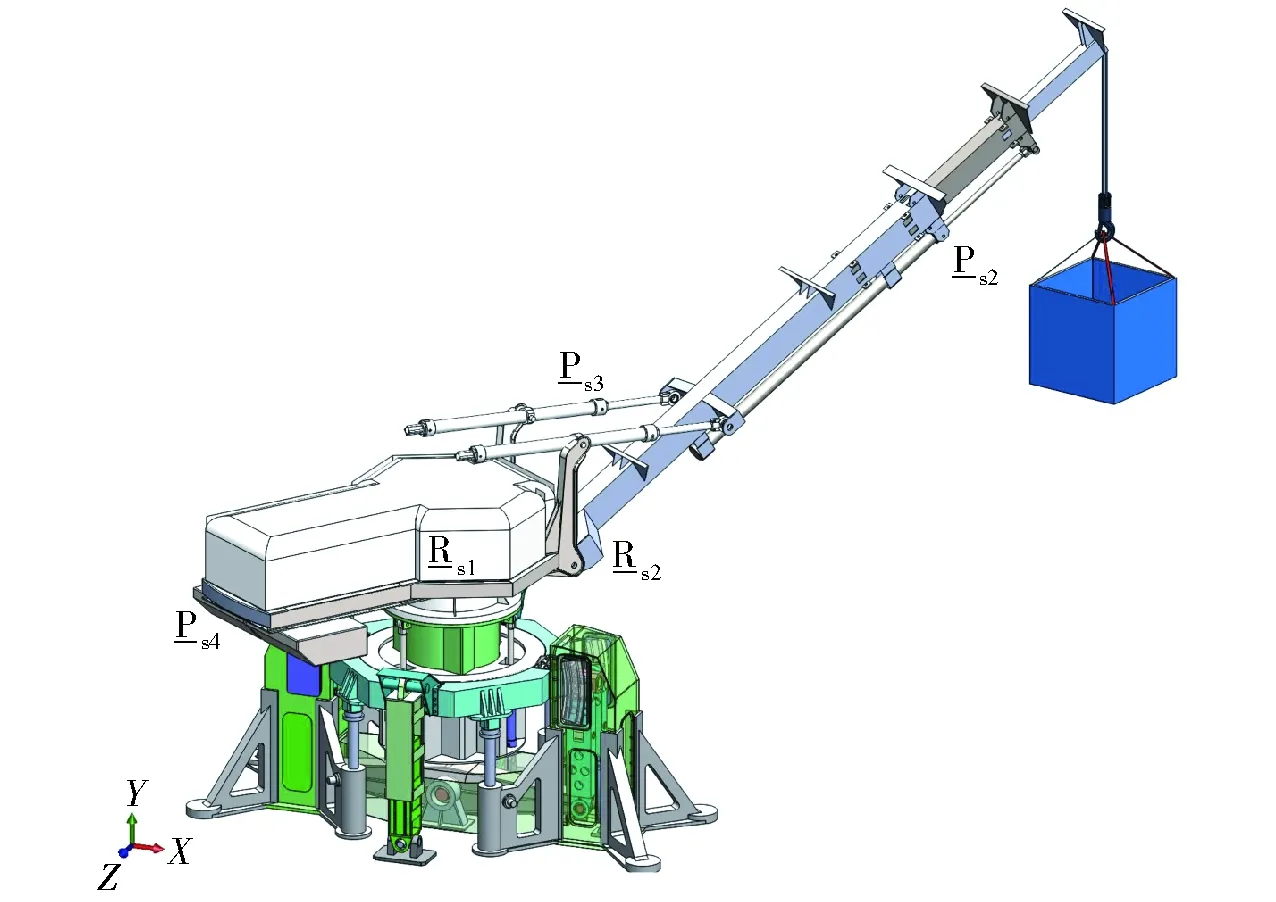
图8 混联稳定克令吊三维造型 Fig.8 3-D model of hybrid stable crane

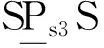
不考虑各驱动的质量及惯性力，忽略摩擦力，给定重力加速度为g=9.8 m/s2。由于作业船的运动由多阶谐波组成，并可近似用不同正弦波的叠加来描述。为简化起见，假设惯性元件测得其安装处作业船的横摇满足α(t)=6sin(2πt/12)、纵摇满足β(t)=3sin(2πt/12)和垂荡满足h(t)=1.5sin(2πt/12)规律。用Matlab编程可得到一个运动周期内稳定克令吊补偿模式下稳定于吊点时各驱动副的位移、速度、加速度及驱动力随时间变化的曲线，如图9所示。

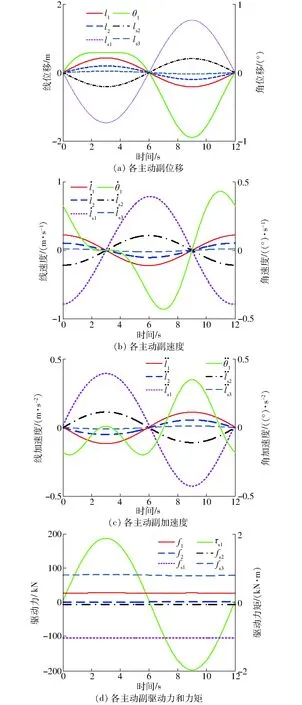
图9 Matlab计算所得曲线 Fig.9 Curves calculated by Matlab

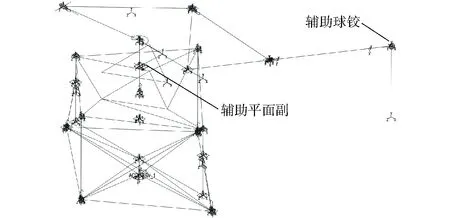
图10 ADAMS稳定克令吊线条模型 Fig.10 Polyline model of stabilizing crane in ADAMS

根据三维造型，在ADAMS中绘制稳定克令吊机构的线条模型，如图10所示，并添加相应的运动副约束、质量和惯量。在下平台{s}系原点与地面之间添加MOTION运动(α(t)，β(t)，h(t))，在中间平台{p}系原点与地面之间添加平面副辅助约束，在伸缩臂吊点与地面之间添加球铰辅助约束，则可实现稳定克令吊稳定于吊点的运动仿真，测出各驱动副(并联部分的第1、2分支)的位移、速度和加速度曲线，与图9a～9c所得曲线对比，可看出两种方法所得运动学曲线完全一致；在后处理界面中把位移曲线创建成样条曲线，去除平面副和球铰辅助约束，在各驱动副处添加相应的驱动，驱动参数采用标准三次样条曲线函数获得。进行动力学仿真，测得各驱动副(并联部分的第1、2分支)的驱动力曲线如图11所示，可以看出两种方法得到的驱动力大致相同，这是因为ADAMS中的动力学仿真，每个构件都必须有质量和惯量，而本文建模只考虑了主要构件的质量和惯量。

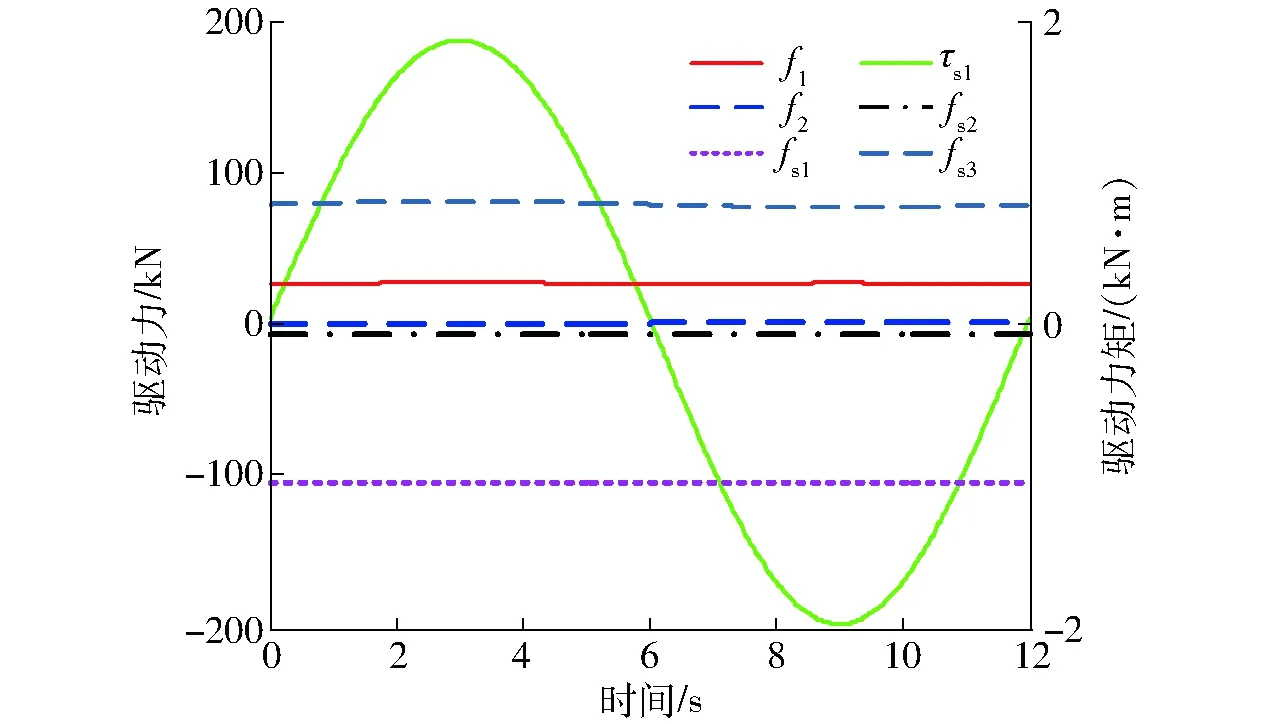
图11 ADAMS仿真所得各主动副驱动力和力矩 Fig.11 Driving force curves measured by ADAMS

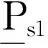
6 结束语

针对船-海上平台之间的货物吊运，提出了一种并串混联稳定克令吊机构，其可以补偿作业船的摇荡并实现吊点处的稳定，保证货物的安全吊运并提高作业窗口时间。建立了稳定克令吊稳定于吊点的运动学及动力学模型，并用数值仿真验证了所建模型的正确性，为此稳定克令吊的工程化应用奠定理论基础。