基于CDM的复合材料缺口强度三维数值仿真模型
2018-08-31王颀吴富强
王颀,吴富强
(南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
0 引 言
复合材料结构应用时,经常需要打孔或开口。缺口的存在破坏了纤维的连续性,改变了结构的传力路线,致使结构因为局部刚度的突变而在缺口附近区域产生应力集中,应力集中处的材料损伤会降低复合材料的结构强度和使用寿命。对于结构设计者来说,理解这种含缺口的纤维增强复合材料的力学性能至关重要。
三维有限元模型可预测复合材料层合板层内和层间不同的损伤模式,可模拟损伤起始、扩展直至层合板失效的整个过程。但预测结果的好坏取决于损伤模式的组合与区分、损伤失效判定准则的选择以及不同模式损伤发生后材料属性的退化方式。
国内外引用较多的三维渐进失效分析数值建模方法主要有:
国内,鲁国富等[1]建立了复合材料含孔层合板的三维有限元模型,模型考虑了剪切非线性,损伤起始判定采用修正后的Hashin-3D准则,采用弹性常数直接折减策略对材料属性进行退化;王跃全等[2]为了模拟含中心圆孔层合板的拉伸失效分析,建立了三维复合材料层合板渐进损伤非线性分析模型;李沛城等[3]建立了基于连续介质损伤力学的三维复合材料层合板模型,并用于复合材料开口层合板的损伤破坏分析;关志东等[4-5]建立了复合材料含开孔层板拉伸和压缩的三维分析模型,采用Hashin-Rotem准则判定失效,失效发生后对相关材料属性采用瞬间退化的策略,层间插入界面单元模拟分层损伤并引入A.Turon等[6]的界面单元网格尺寸处理技术;唐玉玲等[7]建立了三维模型,对双边半圆切口、中心开孔和双边V型切口三种结构进行了静态拉伸试验和有限元模拟分析,比较了不同开孔/切口形式C/C编织型复合材料的破坏行为;崔海坡等[8]应用三维渐进损伤分析技术,对含孔复合材料层合板在压缩载荷下的破坏过程进行了分析;刘魏光等[9]针对具有明显剪切非线性的复合材料,提出一种考虑剪切非线性影响、能够分析和预测复合材料层合板极限承载能力的损伤模型。
国外,B.G.Falzon等[10]根据复合材料单层失效机理,提出了一个三维分析模型,该模型基于连续损伤力学,采用Puck理论判定材料损伤起始,建立了基于能量释放率表达的材料属性退化模型;S.R.Hallett等[11]研究了含中心圆孔的准各向同性层合板,测试了改变铺层次序和几何尺寸时,试件失效强度和失效模式的变化;D.C.Pham等[12]建立了渐进失效模型来模拟准各向同性双边开口层合板,模型采用了材料属性退化和内聚力模型结合的方法,同时比较了应用Tsai-Wu准则、Christensen准则、细观力学准则、损伤力学准则、改进后的损伤力学准则和改进后的Christensen准则等不同层内失效准则对预测最终失效强度的影响;B.N.Nguyen[13]应用三维渐进损伤方法分析了复合材料层合板的破坏过程,失效分析采用了最大应变准则;K.I.Tserpes等[14]以P.P.Camanho的研究为基础,在对螺钉接头的失效分析中,提出了拉伸载荷作用下的三维渐进损伤模型,该模型分别考虑了纤维断裂、基体开裂和分层,但没有考虑基纤剪切破坏(脱胶)等失效模式。
本文基于连续介质损伤力学提出一个预测复合材料缺口强度的三维数值模型,用内聚力接触属性模拟层间损伤,完成[0/902/0]S和[0/90/±45]S开孔层合板拉伸强度数值分析,并将模拟结果与文献中的仿真结果和试验结果进行对比。
1 传统CDM模型的局限性
为了模拟各损伤模式的起始和演化,国内外已探究了大量基础本构模型和数值仿真方法,且取得了丰硕成果。在连续损伤力学(CDM)框架内,对层间损伤模式进行初步的研究,研究广泛应用于界面建模技术,例如粘聚区模型和虚拟裂纹闭合技术(VCCT)[15-16]。尽管在渐进式损伤建模方面取得了一些进展,但最近的研究表明,连续损伤力学[17-18]模型在判定包含粘聚区模型模拟的分层失效时,很难准确地表示出基体开裂与分层之间存在的相互影响、耦合现象。在CDM方法中,用局部刚度退化的方式模拟裂纹产生,而在现实情况中,当裂缝起始时,应力传递本不应该穿过裂缝表面。E.V.Iarve等[19]表示,由于存在虚假的应力转移,局部应力分布在损伤附近没有准确预测。此外,K.Song等[20]指出,由于剪切锁死,网格排布会影响基体裂纹扩展方向,即基体开裂更倾向于沿着网格边缘或网格对角线方向扩展,如图1所示。
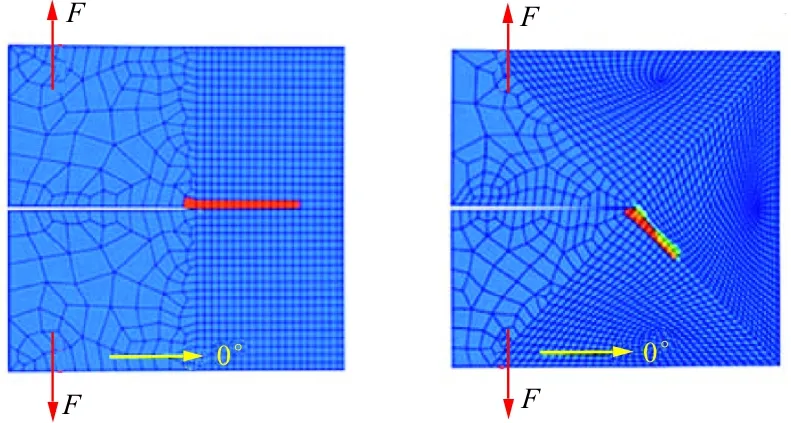
(a) 正向裂纹网格 (b) 斜向裂纹网格
基于均质化建模的特点,模型消除了纤维和基质之间的区别,传统的CDM模型难以预测裂纹路径,无法判别沿纤维方向扩展的裂纹。在采用损伤定位的CDM模型中,任何积分点的损伤状态只依赖于该点的应力场,而不是相邻点的损伤状态。因此,损伤演化的方向只能由瞬时局部应力分布来决定。即损伤判据也许可以正确预测局部的裂纹方向,但是如果在损伤模型中没有恰当地解释材料形貌,那么在宏观上,裂纹路径就可能会被错误地预测。CDM模型的网格依赖性也导致了预测裂纹路径的困难。在有限元模拟中,损伤倾向于沿网格边缘或对角线扩展。在研究中观察到的剪切锁死、虚假应力传递和网格依赖性问题,可以通过将网格边缘与裂纹方向对准来缓解。J.Wang等[21]实验观测到基体裂纹平行于纤维方向。因此,为了更准确地模拟基体裂纹,应使每层网格排布与纤维方向一致,这就要求各层网格结构需不一样。本文采用光透法观察玻璃纤维增强树脂基复合材料开孔层板在拉伸加载过程中的损伤起始及演化(如图2所示)。配合微距拍摄、光透法等手段重点观测孔边开裂路径及演化方式。

(a) [±45]4S (b) [0/90]4S
分别划分放射形网格和对齐网格,在应力集中区域内预测的损伤区域如图3所示,可以看出:两种网格模型都能预测出与孔边的纵向劈裂,采用放射形网格预测的峰值负荷明显低于对齐网格预测的峰值负荷,其原因可能是放射形网格没有准确地描述复合材料开孔件的应力松弛区;所得结果与排列的网格表明,孔边沿纤维方向的纵向劈裂对孔的应力集中有缓解作用。利用放射形网格对描述孔边缘的应力松弛现象有所欠缺,而对齐网格可以较好地模拟由应力松弛区与材料拉紧区之间的剪切力造成的缺口尖端纵向劈裂,也能较好地模拟这一现象对孔边应力集中的缓解作用。
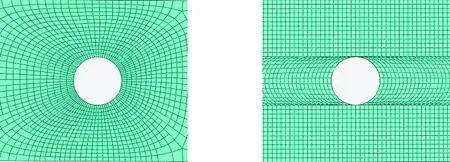
(a) 放射形网格 (b) 对齐网格
2 三维数值仿真模型
2.1 有限元仿真分析流程
对于含缺口层合板的失效分析,由于其层内损伤和层间损伤耦合存在、相互影响,导致其层内和层间三维应力分析、单元损伤起始判定、单元损伤演化同时进行;其失效过程可看作是一个准静态加载下的损伤演化过程,在有限元模拟过程中施加位移载荷;层内采用三维实体单元建模,层间引入内聚力接触属性。由此可得本文含缺口复合材料层合板渐进损伤数值分析流程,如图4 所示。
2.2 层内损伤分析模型
层内的起始破坏准则选用区分失效模式的三维Puck准则[22],损伤演化准则采用基于能量的线性退化方式,由VUMAT用户子程序来预测纤维拉伸失效(FFT)、纤维压缩失效(FFC)、纤维间拉伸失效(IFFT)和纤维间压缩失效(IFFC)四种失效模式。对于纤维断裂损伤,考虑到纤维脆性较强,在断裂时能量会瞬间释放,本文采用直接折减策略对复合材料的弹性常数进行退化。对于纤维间失效的预测,采用A.Puck基于Mohr和Coulomb理论提出的具有物理含义的纤维间失效准则判定,该准则认为纤维间失效与否与潜在断裂面上的应力相关。对于纤维间失效,材料释放能量的过程相对缓慢,本文采用逐渐卸载模型中的线性软化[23]模型描述失效后的材料性能。模型认为损伤起始后,材料的性能服从线性等效应变-软化行为,且损伤演化速率取决于损伤区域内材料的临界应变能量释放率。
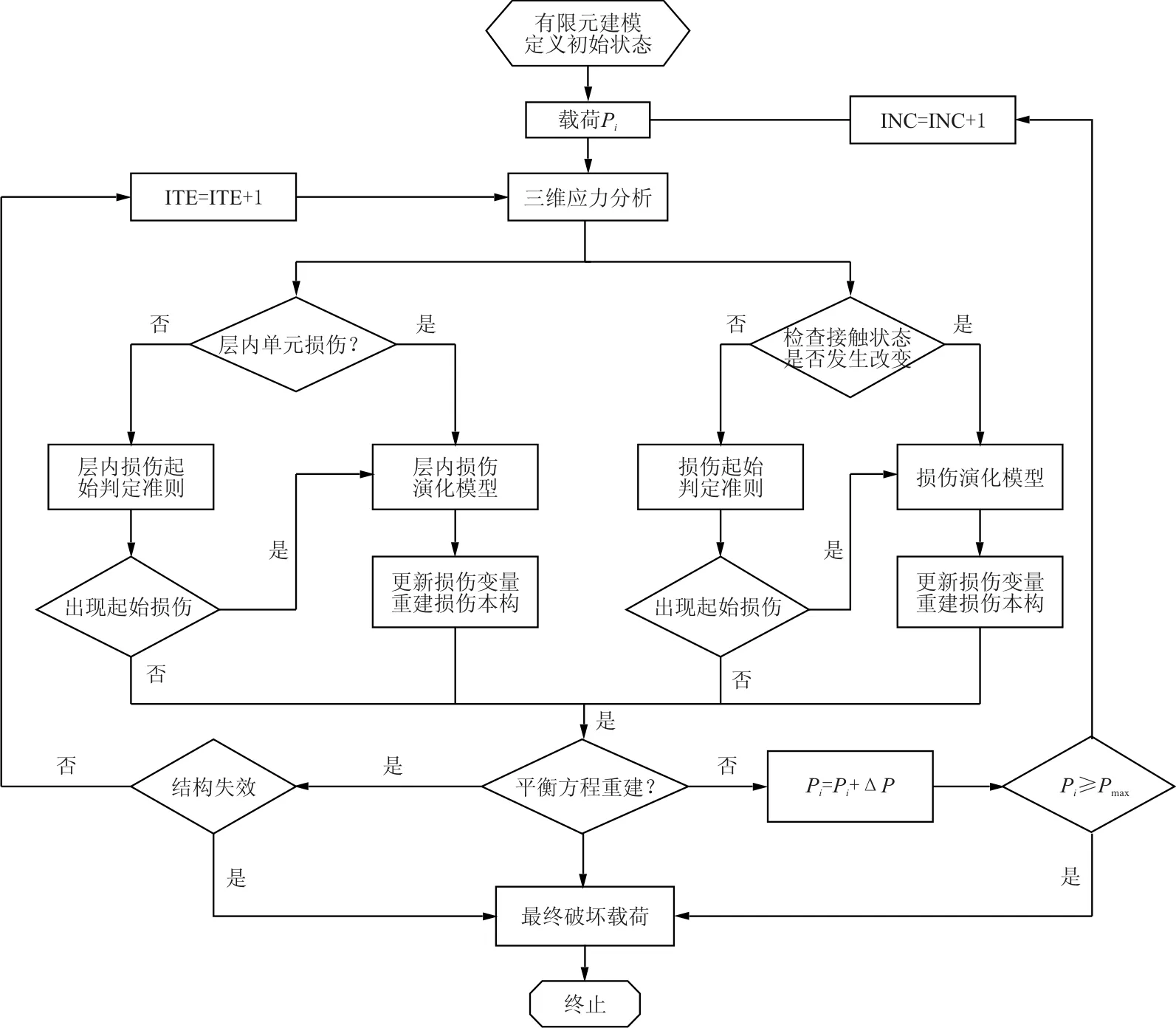
图4 FRP静力加载仿真模型Fig.4 Flow chart simulating damage of FRP
2.3 层间损伤分析模型
在有限元模型中采用内聚力接触(Surface-based Cohesive Behavior)定义层间粘聚区,基于表面的内聚力接触与内聚力单元的功能相似。再将粘聚区的本构关系引入到有限元模型中,进而实现对层间分层损伤萌生和扩展的模拟。粘聚区模型的本构关系是基于牵引-相对位移(Traction-Relative Displacement)关系定义的。
不考虑各轴向耦合效应时,完好层间界面元的本构关系为
(1)
在判定层间分层萌生的准则中,最常用的准则是基于应力表达的二次准则,该准则考虑了拉应力对分层萌生的促进作用,其表达式为
(2)
模型中采用混合模式的B-K[24]能量释放率准则预测分层损伤的扩展行为,其表达式如式(3)所示。当材料的释放率满足损伤扩展准则时,材料完全失效。
(3)
在ABAQUS/Explicit显示求解中,内聚力接触可以被定义为通用接触(General Contact),是一种面之间的相互作用。内聚力接触基于牵引-分离(Traction-Separation)模型(如表1所示),为模拟厚度可以忽略的粘性连接提供了一种简便的方法。为了避免过度约束,必须采用单纯主从算法。内聚力接触所遵循的函数、准则与内聚力单元基本相同,但两者对牵引和分离的解释不同。

表1 牵引-分离模型Table 1 Traction-separation model
在内聚力接触的定义中,损伤是作为连接相互作用的一部分来指定的。对于基于面的内聚力行为,采用粘性刚度退化来描述损伤演化,与之对应的内聚力单元,采用材料刚度退化来描述损伤演化行为。内聚力接触是一种接触属性,而不是材料属性。内聚力接触的定义过程很简单,使用接触的相互作用和内聚力相互作用属性,约束加载于从属节点上。对于粘结界面,厚度可以忽略不计,只允许一种失效形式。内聚力接触行为结合默认的粘性刚度属性,对稳定时间增量影响很小。
3 算 例
应用ABAQUS建立了AS4/3502Gr/Ep纤维增强复合材料层合板[/0/902/0]S、[0/90/±45]S的三维有限元模型,模拟其开孔拉伸的破坏。该模型采用ABAQUS显式分析算法,自编VUMAT子程序,加载速度足够小使得模型中的动能可以忽略不计。对于AS4/3502Gr/Ep纤维增强复合材料层合板,其性能参数及内聚力接触的材料参数分别如表2~表3所示[25]。由于该材料的对称性,每一种层合板只模拟四层。
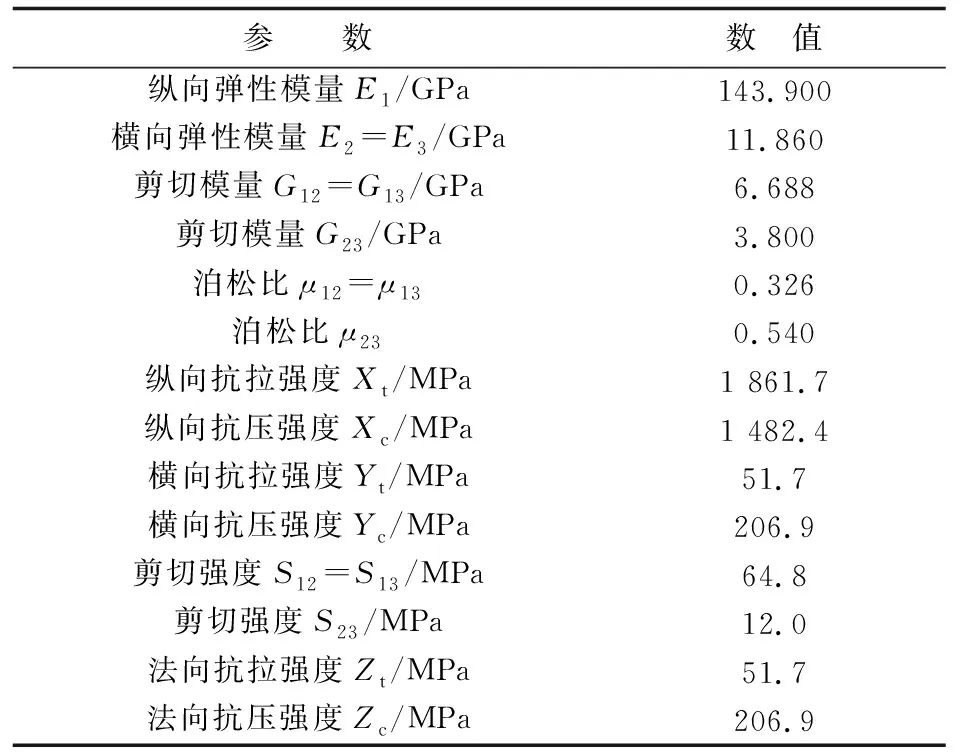
表2 AS4/3502Gr/Ep复合材料的性能参数Table 2 Material properties of the unidirectional AS4/3502Gr/Ep laminate

表3 AS4/3502Gr/Ep内聚力接触的材料参数Table 3 Material properties of the AS4/3502Gr/Ep cohesive behavior
模型为矩形,长80 mm,宽30 mm,每一层厚度0.125 mm。层合板正中心开圆孔,圆孔半径4.5 mm。
在有限元模型中,每一层均采用三维实体单元(C3D8R)。且每层采用不同方向的网格(如图5所示),使网格边缘与纤维方向平行。同时用内聚力接触来模拟层间的分层损伤。

(a) 45°层 (b) -45°层

(c) 90°层 (d) 0°层
图5 复合材料层合板有限元模型各层的网格
Fig.5 Finite element mesh for each layer of composite laminates
3.1 [0/902/0]S模拟结果
本文数值模型模拟[0/902/0]S层合板的载荷-位移曲线如图6所示,可以看出:有限元模拟的最终失效应力为399.9 MPa。试验所得的最终失效应力为441.6 MPa[25],本结果与试验值的误差为9.4%;文献[25]最终失效应力的计算值为486.0 MPa,与试验值的误差为10.2%,故可以认为本文模拟取得了较好的结果。
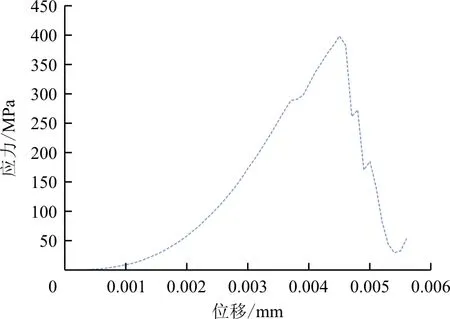
图6 [0/902/0]S铺层的载荷-位移曲线Fig.6 Stress-displacement curve of [0/902/0]S laminates
[0/902/0]S的损伤演化过程如图7所示。

(a1) 90°(IFFT) (a2) 0°(FFT)
(a) 损伤起始

(b1) 90°(IFFT) (b2) 0°(FFT)
(b) 损伤扩展
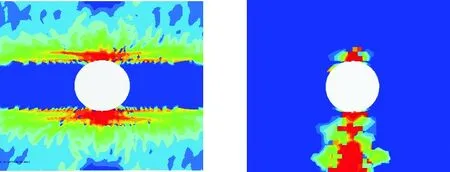
(c1) 90°(IFFT) (c2) 0°(FFT)
(c) 最终失效
图7 [0/902/0]S含中心圆孔层合板拉伸载荷下损伤演化过程
Fig.7 Process of damage evolution under tensile load of [0/902/0]Snotched laminates
从图7可以看出:损伤首先出现在90°层,为纤维间损伤,之后损伤扩展,载荷加至大约93%失效载荷时,0°层出现纤维断裂,并沿垂直于载荷的方向扩展至自由边界,层合板整体发生破坏,90°层发生大面积纤维间损伤。
本文数值模型模拟得到层合板的破坏模式如图8(a)所示,试验所得相同铺层层合板的破坏模式如图8(b)所示,对比二者,可以看出:数值模拟与试验结果较为相符,表明模型可以较准确地模拟层合板的破坏模式。

(a) 数值模拟结果 (b) 试验观察到的结果
3.2 [0/90/±45]S模拟结果
本文数值模型模拟[0/90/±45]S层合板的载荷-位移曲线如图9所示,可以看出:有限元模拟的最终失效应力为296.5 MPa。试验所得的最终失效应力为325.9 MPa[25],本文结果与试验值的误差为9.0%;文献[25]最终失效应力的计算值为370.1 MPa,与试验值的误差为13.56%,故可以认为本文模拟取得了较好的结果。
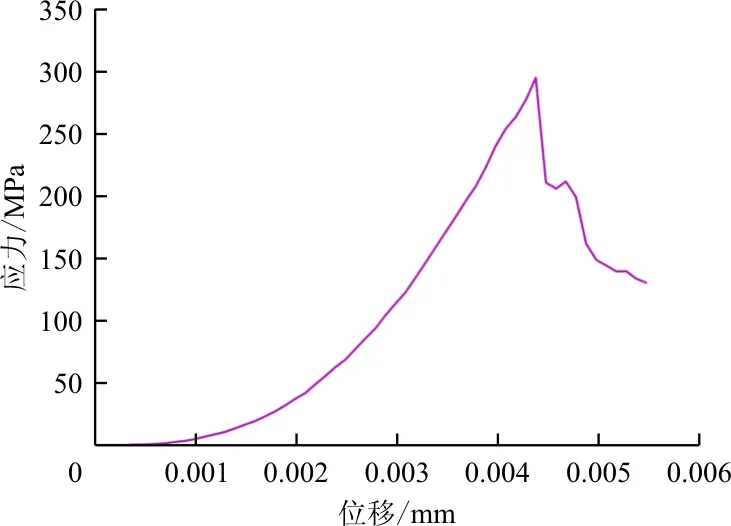
图9 [0/90/±45]S铺层的载荷-位移曲线Fig.9 Stress-displacement curve of [0/90/±45]s laminates
[0/90/±45]S的损伤演化过程如图10所示。

(a1) 90°(IFFT) (a2) 45°(IFFT) (a3) -45°(IFFT) (a4) 0°(FFT)
(a) 损伤起始

(b1) 90°(IFFT) (b2) 45°(IFFT) (b3) -45°(IFFT) (b4) 0°(FFT)
(b) 损伤扩展

(c1) 90°(IFFT) (c2) 45°(IFFT) (c3) -45°(IFFT) (c4) 0°(FFT)
(c) 最终失效
图10 [0/90/±45]S含中心圆孔层合板拉伸载荷下损伤演化过程
Fig.10 Process of damage evolution under tensile load of [0/90/±45]Snotched laminates
从图10可以看出:损伤首先出现在90°层和±45°层孔边,为纤维间破坏,之后0°层出现纤维断裂,加至大约95%失效载荷时,45°层开始出现纤维断裂,0°层纤维断裂逐渐扩展至自由边界,层合板整体破坏。
4 结 论
(1) 探讨了传统CDM模型的局限性,比较了放射形网格和对齐网格对同一模型的数值模拟结果。对齐的网格可以更好地描述复合材料的破坏模式,也能较好地模拟孔边应力集中的缓解现象。
(2) 为了更好地反映复合材料的力学特性,并实现层合板每一层中划分沿纤维方向的网格,在层间引入内聚力接触。内聚力接触属性可以较好地模拟复合材料分层损伤;该模型可以预测不同材料体系和铺层参数的层合板在拉伸载荷作用下的损伤破坏过程及失效载荷。
(3) 自编VUMAT子程序,应用区分纤维失效和纤维间失效的PUCK准则,建立三维渐进损伤分析模型,可以较准确地模拟含孔复合材料层合板在拉伸载荷作用下的逐渐破坏,且该方法的预测精度较高。
