典型布局飞机电磁散射特性数值计算研究

刘战合，王菁，姬金祖，王晓璐，赵辉

(1.郑州航空工业管理学院 航空工程学院，郑州 450046)(2.北京航空航天大学 航空科学与工程学院，北京 100191)

0 引 言

隐身技术现已成为飞行器设计的主要技术组成，对于直接参与执行战场任务的飞行器、装甲车辆、兵器等[1-3]，其隐身性能的优劣将在很大程度上决定武器系统的生存能力和作战效能[4-6]。以飞行器为例，可用来探测的信号主要包含电磁、红外、可见光、声音等，信号的强弱体现了飞行器在该信号上的隐身性能。隐身技术也相应的分为电磁、红外、可见光和声隐身等方面[2]。

执行不同任务的飞机具有不同的布局形式，从飞行器设计角度来讲，不同的任务具有不同的机动性、气动特性、载荷性能、飞行性能、成本要求等[2,7-8]。对于作战及作战支援飞机，不同的任务需求使得飞机的隐身性能存在较大差异。岳奎志等[7-8]从双立尾、挂载导弹等角度研究了战斗机的隐身特性；焦予涵等[9]研究了飞行器气动隐身优化方法。但基于飞机布局来研究隐身性能的文献仍较少。

本文通过对现有作战飞机进行梳理分类，对典型布局飞机的隐身性能从其电磁散射布局特点、频率响应特性等方面进行详细研究，建立布局形式、雷达散射截面(Radar Cross Section，简称RCS)分布特点以及隐身性能等之间的对应关系，以期为飞行器隐身设计和改进工作提供有益参考。

1 电磁计算模型建立

作战飞机一般分为战斗机、轰炸机和战斗轰炸机。当前飞行器种类繁多，非隐身常规布局战斗机有美国的F-16、F-18，俄罗斯的Su-27、Mig-29，中国的J-10等；隐身型常规布局飞机有美国的F-22、F-35，中国的J-20、J-31，俄罗斯的T-50等；飞翼布局飞机有美国的隐身轰炸机B-2、X-47B、X-45A等；此外，还有设计之初以电磁隐身指标为主要技术目标的F-117。

为了详细研究各种目标飞行器的隐身性能及RCS分布特点，将上述四类飞机布局定义为：①布局A：非隐身常规布局，此类布局以当前主流战斗机为基本模型，兼顾轻、重型布局形式；②布局B：隐身型常规布局，此类布局以当前典型隐身战斗机为基准形式；③布局C：飞翼布局，此类布局是隐身轰炸机和无人攻击机的重要布局形式；④布局D：特殊布局，一些以隐身性能为首要目标的飞行器仍占一定比例，典型的比如F-117。电磁建模时，其关键几何参数参考各类典型飞行器型号。

对布局A，分别建立了常规单垂尾的轻型战斗机电磁模型A-1和双垂尾的重型战斗机电磁模型A-2；对布局B，以隐身战斗机F-22为参考建立电磁模型B；对布局C，以美国的B-2为参考建立飞翼电磁模型C；布局D，以美国的F-117为基础，定义为电磁模型D。各电磁模型如图1所示。

(a) 电磁模型A-1 (b) 电磁模型A-2

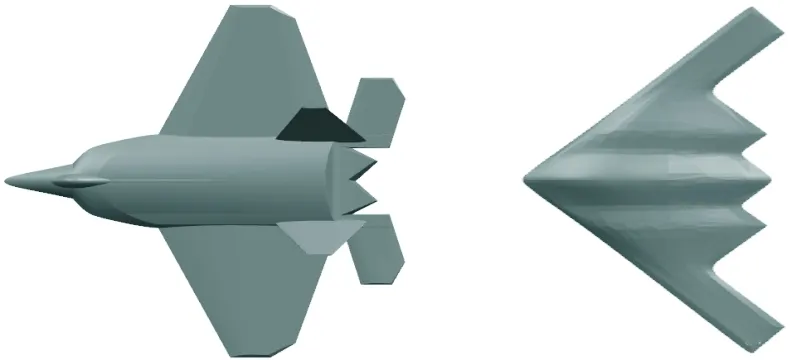
(c) 电磁模型B (d) 飞翼电磁模型C

(e) 电磁模型D图1 各电磁计算模型俯视图Fig.1 Electromagnetic models of aircraft

所有模型均采用实体方式，兼顾模型真实性和电磁计算方法要求，表面曲率光滑。一般的，飞机面临的电磁波探测频率在S、C、X、Ku、K等波段，本文以X波段10 GHz为主要研究频率。从布局特点可以看出，A-1和A-2属于非隐身飞机，其他布局形式均为隐身飞机，针对多频特性和俯仰角特性，以电磁模型A-1和D为研究对象，兼顾3、18 GHz两个波段。所有电磁波入射角变化范围为0～360°。同时，结合曲线分布形式，分别以前向30°(-15°～15°)、侧向30°(75°～105°)、后向30°(165°～195°)、周向(0～360°)各角域为研究对象，分析相应布局的电磁散射特性。

2 RCS数值方法及精度验证

2.1 RCS数值计算方法

用于飞行器电磁散射的计算方法主要分为积分、微分和有限元法等，其中积分方法具有精度高的优点，该方法又可以分为高频和低频两种计算方法。物理光学法(Physical Optics，简称PO)[7-8]、矩量法(Method of Moments，简称MOM)[10-11]、多层快速多极子算法(Multilevel Fast Multipole Algorithm，简称MLFMA)[12-16]属于积分方法，均以Stratton-Chu积分方程为基础，基本方程分为电场积分方程和磁场积分方程。

物理光学法属于高频方法，而矩量法及其快速算法——多层快速多极子算法和快速多极子算法为低频算法。低频算法(例如矩量法)通过求内积将Stratton-Chu积分方程变为可数值求解的方程组，其系数矩阵不仅考虑了自身的强耦合作用，也考虑了目标各部分之间的相互影响，计算时占用内存大、计算效率低，但精度高。相比而言，物理光学法具有较高的计算效率，仅考虑自耦合作用，忽略各部分之间的相互作用，尤其对本文整机光滑目标而言，对电大尺寸(即高频区)目标，例如飞行器等仍具有较高的计算效率和精度。

尽管出发点是Stratton-Chu积分方程，但物理光学法根据高频散射的局部性原理以及入射电磁场直接计算表面感应电流，进而求出RCS，忽略了面元之间的弱耦合作用，面元间的感应电流相互影响忽略不计。采用切平面近似，得到该研究面元上的RCS平方根[7-8]为

(1)

基于目标网格划分，对所有散射面元求和，按相位叠加可得

(2)

2.2 PO和MOM计算精度对比

为了验证物理光学法的计算精度，以金属立方体为研究对象，分别采用物理光学法和高精度矩量法计算其RCS曲线，结果对比如图2所示。

图2 金属立方体RCS计算对比曲线Fig.2 RCS comparison curves of metal cube

立方体边长1 m，入射电磁波波长0.1 m，俯仰角0°，矩量法(MOM)的计算结果为水平极化。从图2可以看出：物理光学法与矩量法RCS计算曲线吻合较好，物理光学法0～45°角域算术均值为16.652 1 dBsm，矩量法为16.593 6 dBsm，全向误差为0.058 5 dB，表明物理光学法有足够好的计算精度，尤其是物理光学法在高频散射区对复杂散射体区有较高的计算效率，适用于本文研究对象和计算频率。

3 不同布局目标RCS分布特性

3.1 RCS曲线分布特性

针对上述四类典型布局的五个飞机电磁模型，入射电磁波频率为10 GHz，其RCS计算曲线依次如图3～图6所示，考虑到电磁模型A-1和A-2均属布局A，二者RCS曲线如图3所示。

图3 布局A电磁模型RCS曲线Fig.3 RCS curves of electromagnetic models for layout A

电磁模型均未考虑外挂物，即外挂的导弹、副油箱等，主要研究飞机布局对电磁散射的影响。对于常规布局A，从图3可以看出：RCS曲线具有一定的共性，在前向、两个侧向、尾向均存在对应的散射波峰，波峰宽度较窄，幅值较高，散射曲线整体上呈“菱形”或“矩形”分布，且其“菱形”对角线即为机身轴线或其垂线(即侧向)；前向波峰为机头的前向散射贡献，尾向波峰为机翼后缘、尾部发动机位置的综合散射贡献。

同时，由于飞机外形存在较大区别，模型A-1的电磁散射曲线在周向分布有多个波峰，在前向左右50°附近存在一尖锐波峰，该波峰为机翼前缘散射效果，即垂直于机翼前缘方向，同时尾向左右15°附近存在两散射波峰；而模型A-2在周向处除有明显的“菱形”四个波峰外，无次波峰，这是由于对该模型的所有机翼前缘和后缘进行了尖劈处理，以与A-1形成对比。可见，机翼及鸭翼的隐身改进对RCS的精细分布有一定影响，提高了隐身性能，降低了周向次波峰。

综上所述，对常规布局A，RCS散射在周向呈“菱形”分布，且四个散射波峰位于前向、侧向和后向，不具备隐身性能，尽管可以通过尖劈化处理来降低机翼等结构的散射效果，但对常规布局A，影响其隐身性能的重要角域在前向角域，因此，该布局类型主要讨论前向隐身性能。

对布局B，电磁模型B的RCS计算曲线如图4所示。

图4 布局B电磁模型RCS曲线Fig.4 RCS curves of electromagnetic models for layout B

从图4可以看出：尽管采用类似的常规布局，但对其机身、机翼、机头等重要位置进行了外形隐身设计，其RCS散射曲线出现了较大的不同，为了提高隐身性能，其前向和尾向波峰均被剥离成左右两个波峰，分别对应机翼前缘、后缘垂直方向，提高了前向和后向隐身性能；其侧向RCS峰值为机身及机翼等对侧向的散射作用，侧向峰值的产生类似于常规布局A。从RCS整体分布来看，具有外形隐身技术的常规布局B，其RCS近似呈“米字形”分布，且前向和尾向波峰较低或无波峰，有利于实现隐身，亦是隐身性常规布局战斗机的典型特性。

对飞翼布局C，电磁模型C的RCS计算曲线如图5所示，可以看出：与布局A和布局B相比，该图曲线分布中侧向波峰向内压缩、幅值减小。由于该电磁模型C作战以隐身轰炸为主，并不具备空中作战能力，因此其气动布局可采用飞翼布局，有效降低了周向RCS。其前向和尾向RCS在-10 dBsm以下，有较高的隐身性能，观察其周向分布，各RCS波峰幅值也较小；整体来看，RCS周向均在10 dB以内，而常规布局的电磁模型A和B周向幅值均较高。

从RCS分布角度来看，布局C电磁模型的RCS曲线呈近似“蝶形”分布，具有蝴蝶形的外形特点，即前向、尾向较小，侧向峰值向内压缩，由于整体幅值偏小，并未形成尖锐的波峰。这一分布特点是综合考虑了前向、尾向及周向隐身性能的一种方式，接近于实现全周向隐身，但由于布局特点，该布局在气动特性、控制特性上有所牺牲，并不适合机动要求高的作战任务。

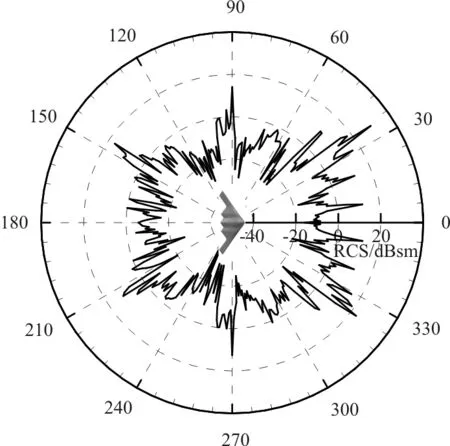
图5 布局C电磁模型RCS曲线Fig.5 RCS curves of electromagnetic models for layout C

电磁模型D的RCS曲线如图6所示，该模型采用典型的外形隐身技术，机翼前缘、后缘平行，不同后缘位置尽量以平行方式设计，其机身表面几乎无曲面，均以相互平行的平面拼接而成，成功将RCS波峰集中在少数几个位置。

图6 布局D电磁模型RCS曲线Fig.6 RCS curves of electromagnetic models for layout D

从图6可以看出：布局D的RCS曲线形式与布局C类似，更接近于“蝶形”，其前向和尾向RCS相对幅值更低，接近-30 dBsm，沿机身轴线对称分布的几个波峰，例如方位角68°、80°、127°附近存在散射波峰，构成典型“蝶形”分布形式，以上几个波峰分别为该模型的机翼前缘、后缘的垂直方向的综合表现。而从周向RCS幅值来讲，由于采用平行分布的平面可将入射电磁波向可控的方向散射，降低了俯仰角0°时周向RCS的幅值，比飞翼布局分布的模型C整体偏小，隐身性也较好。

3.2 各角域算术均值分析

上述四种布局电磁模型的头向、侧向、尾向和周向RCS算术均值分别如表1所示，入射电磁波频率10 GHz、俯仰角0°。

表1 RCS各角域算术均值表Table 1 RCS arithmetic means in different angle domains

从表1可以看出：不同布局飞机由于其RCS散射曲线分布形式各有区别，在四个角域(即前向、侧向、尾向、周向)上的RCS算术均值均有差异。在前向角域，对常规布局A的两个电磁模型，其RCS算术均值比较接近，为7 dBsm左右；经过外形隐身设计后，常规布局B在前向具有优秀的隐身性能，均值降低为-10.434 7 dBsm，前向隐身性能获得提高；对飞翼布局C，尽管模型C具有较大的几何尺寸，其前向角域RCS算术均值仍较低，为-6 dBsm左右；以隐身设计为主要目标，采用平板拼接方式设计的模型D，其电磁散射在前向由于较好的控制得到了大幅降低，达到-30.067 3 dBsm。

在侧向角域，布局A、B的三个模型算术均值基本接近，表明常规布局形式对侧向影响不大，飞翼布局模型C在侧向表现优秀，模型D在侧向也具有一定隐身性能。对于后向，由于机翼形式、尾向布局形式、尾喷口处理方式等对RCS均有影响，后向表现为模型A-1、A-2、B、C、D依次降低，隐身性能随之提高。对于周向，常规布局A和B的三个模型，其RCS算术均值较为接近，在相同量级上，表明外形隐身对周向贡献不大，仅实现能量即波峰方向控制；而模型C和D由于布局对外形做了更进一步处理，表现为更优秀的周向隐身性能，模型D最低，为-15.137 3 dBsm。

布局A-1、A-2、B、C、D不同角域的RCS算术均值曲线如图7所示。

图7 不同布局不同角域RCS均值Fig.7 RCS arithmetic means in different angle domains for different layouts

从图7可以看出：对于布局A-2、B、D，其侧向RCS均值较大，而对飞翼布局C，侧向RCS均值较小，这一特点与其布局方式有关，前向、侧向、后向对入射电磁波来说，有效散射面积接近；对前向和后向，外形隐身效果较为明显，布局D最为优秀；同时，常规布局飞机(布局A-1、A-2、B)的RCS均值特性接近，但经过外形隐身设计后的B在前向和后向具有更为优秀的隐身性能，可满足执行作战任务的要求。

4 电磁散射频率响应特性

飞行器执行任务过程中，会面对来自不同方位不同频率的探测器(即雷达)，因此，有必要研究飞机在主要频率上的电磁散射特性。计算频率分别为3、10、18 GHz，涵盖S～Ku波段。

以常规布局电磁模型A-1、特殊布局模型D为研究对象，其RCS计算曲线分别如图8～图9所示。模型A-1代表常规布局，模型D代表隐身布局。入射电磁波频率由3 GHz增加到18 GHz时，其电尺寸增加到原来的6倍，但均为高频散射区，符合物理光学法的应用范围。

图8 电磁模型A-1多频RCS曲线Fig.8 RCS curves of electromagnetic models for layout A-1 in different frequency

图9 电磁模型D多频RCS曲线Fig.9 RCS curves of electromagnetic models for layout D in different frequency

从图8～图9可以看出：在频率逐渐升高时，散射曲线分布形式对两种电磁模型来说，变化较小，以上现象说明，频率的变化不会引起模型RCS散射曲线分布形式的较大变化，其峰值位置基本不变。结合前述分析可知，RCS散射曲线分布形式与布局特点有直接关系，处于高频散射区时，频率的变化仅影响RCS震荡形式和幅值大小。

为了进一步分析频率对RCS幅值的影响程度，以对应角域RCS算术均值进行研究，如表2所示。表中所取的三个频率为实际飞行器执行任务面临的主要威胁频域，但从电尺寸角度讲，对本文的电磁模型，均在高频区域。

表2 两模型不同频率RCS各角域算术均值表Table 2 RCS arithmetic means of two models in different frequency

从表2可以看出：在高频区域，电磁波依次增加时，各向角域的RCS算术均值整体上表现为减低趋势，布局D更为明显；同时，频率增加时，曲线震荡性增加。

5 结 论

(1) 前向RCS特性：常规布局A-1和A-2前向隐身性能最差，其RCS均值在7 dBsm左右，受其前向峰值影响；布局 B采用隐身设计的常规布局，其前向RCS降低至-10.434 7 dBsm，隐身性能优秀；飞翼布局C和特殊布局D分别为-6.657 3、-30.067 3 dBsm，均具有隐身性能，以特殊布局最优秀。

(2) 后向和周向RCS特性：常规布局A-1和A-2后向RCS均值分别为22.702 5、6.087 5 dBsm，二者区别主要是由于发动机尾喷口形状的影响；布局B、C、D前向RCS均值依次降低，布局D低至-25.093 8 dBsm。周向与后向类似，布局A-1、A-2、B分别为7.039 1、4.725 2、3.604 4 dBsm，常规布局周向RCS较高；C和D分别为-7.928 2、-15.137 3 dBsm，具有较高隐身性。

(3) 布局频率响应特性：对常规布局A和特殊布局D，在高频区域，频率增加时，其RCS分布形式基本不变，震荡性增加，RCS算术均值降低，降低幅值为1～3 dB。