核心素养怎样考(五)
2018-08-30李尚志
李尚志
(北京航空航天大学 100083)
测试题2
题3常数a,b使恒等式a(2x2+x+5)+b(x2+x+1)=x2-3x+13成立,则(a,b)=(__,__).
解恒等式左边合并同类项,整理为:
(2a+b)x2+(a+b)x+(5a+b)=x2-3x+13,
比较等式两边对应项的系数,得待定常数a,b满足的方程
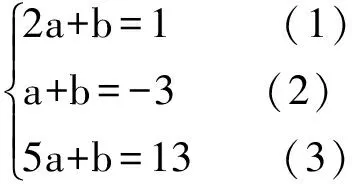
(1)式-(2)式,得:a=4.代入(2)式得:4+b=-3,b=-7.
将a=4,b=-7代入(3)式检验:左边=5×4+(-7)=13=右边.
答案:4,-7.
点评此题很常规.唯一“不正常”的是:每个方程都是二元一次方程,却由三个方程组成方程组.是不是二元一次方程组?是.只要由二元一次方程组成,无论多少个都是二元一次方程组.
怎样求解?很简单:先求出前两个方程的公共解a=4,b=-7.代入第3个方程去检验,等号仍然成立.就是三个方程的公共解.
如果前两个方程的公共解不是第3个方程的解,方程组无解.
这道题看起来意思不大.却是为后面一道题埋下的伏笔.
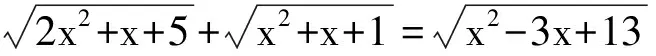
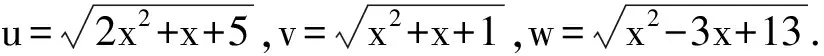
原方程化为u+v=w.易验证
4(2x2+x+5)-7(x2+x+1)=x2-3x+13
(1)
也就是
4u2-7v2=w2=(u+v)2=u2+2uv+v2.
移项,整理得3u2-2uv-8v2=0.
分解因式得(u-2v)(3u+4v)=0
⟹u-2v=0或3u+4v=0.
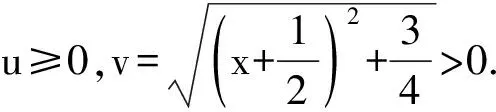
因此3u+4v>0.
只能u-2v=0,u=2v,
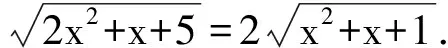
2x2+x+5=4(x2+x+1)⟺2x2+3x-1=0,
借题发挥:线性相关
本题是初中数学竞赛题.初中学生能想出来吗?按初中数学常规思路,两边平方去根号.左边产生一个新根号,其余各项移到右边再平方.化成4次方程,没有有理根.难以求解.以上解法每一步用到的知识确实是初中知识.关键是要想到关系式(1).这个关系式不难验证,却很难把它凑出来.不过,只要想到根号内的3个二次三项式可能有这种关系
a(2x2+x+5)+b(x2+x+1)=x2-3x+13 (2)
就可以解方程求出待定系数a,b.如果方程无解,那就是没有这种关系.
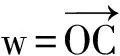
多项式不是几何向量,不能画出图,但也可以做加法,可以乘实数,因此可以看成向量,也可以定义线性相关.考虑到中学生不熟悉线性相关,我的考试题中设计了第3题先让考生算a,b,启发他们利用这个计算结果来做第14题.
第14题能否两边平方去根号,化成有理系数方程求解?不妨一试.
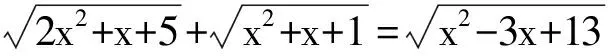
=x2-3x+13,
再平方:8x4+12x3+32x2+24x+20
=4x4+20x3-3x2-70x+49,
移项合并得:4x4-8x3+35x2+94x-29=0
(1)
如果先由前面的解法求出了方程2x2+3x-1=0的两个根是原方程的根,它们也应该是方程(1)的根.2x2+3x-1应该能够整除方程(1)左边.用2x2+3x-1除方程(1)左边得到分解式
(2x2+3x-1)(2x2-7x+29)=0,
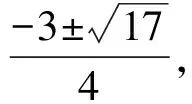
如果没有前面的解法,你能将方程(1)左边因式分解吗?
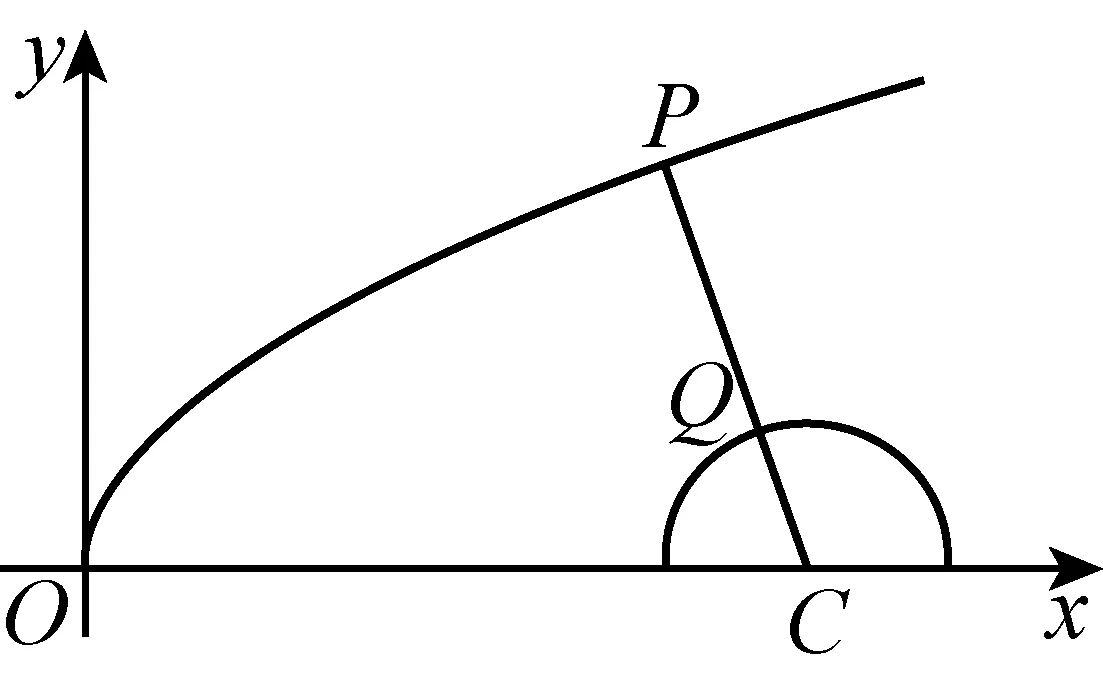
图1
题4P是抛物线
y2=2x上的点,Q是圆
(x-5)2+y2=1上的点,则|PQ|的最小值是________.
解圆心C(5,0)到抛物线上点P(x,y)的距离
|CP|≤|CQ|+|PQ|=1+|PQ|,
因此|PQ|≤|CP|-1.
当|CP|最小,且Q在线段CP上,
则|PQ|=|CP|-1最小.
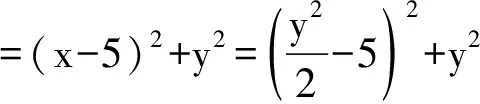
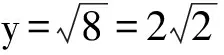
取Q为线段CP与圆的交点,则|PQ|取最小值2.
答案:2

图2
题5使y=
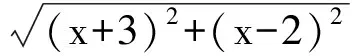
解建立平面直角坐标系xOz.A(1,4),B(-3,2)为定点.如图2.
P(x,x)为直线OC:z=x上的动点.
则y=|PA|+|PB|.
由4>1,2>-3知A,B都在直线OC的左上方.
作A(1,4)关于直线OC的对称点A′(4,1).
则|PA|=|PA′|,A′,B在直线OC的异侧.
当P在直线BA′上时,
y=|PA|+|PB|=|PA′|+|PB|最小.

即(x+3,x-2)=λ(4+3,1-2)=(7λ,-λ).
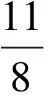
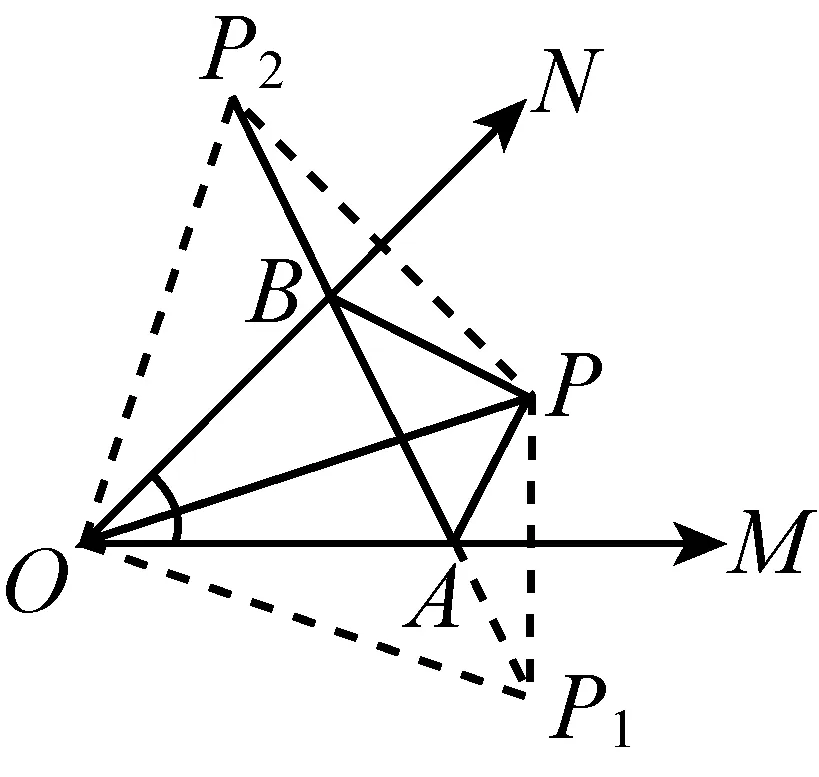
图3
题9P是锐角∠MON=α内固定点,|OP|=r.分别在角的两边OM,ON上选取点A,B使三角形△PAB的周长p最短,则p=________.
解作P关于直线OM的对称点P1,以及P关于直线ON的对称点P2.则|P1A|=|PA|,|BP2|=|BP|,p=|PA|+|AB|+|BP|=|P1A|+|AB|+|BP2|的最短值等于P1到P2的直线距离
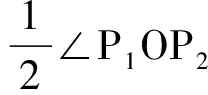
=∠MOP+∠PON=α,
|OP1|=|OP|=r.
因此p的最短值等于|P1P2|=2rsinα.
答案:2rsinα
借题发挥:光的反射定律
填空第5题的要点是看出题中那两个根号是动点P(x,x)到两个定点A(1,4),B(-3,2)的距离|PA|,|PB|.题目要求就是求P到A,B的距离之和的最小值.也就是:从A到直线OC上某一点再到B,沿怎样的路线路程最短?
解答方法也是经典的:作A关于OC的对称点,则路程APB变成A′PB,最短线是直线段A′B,也就是要求∠OPB=∠A′OC=∠AOC.这就是光从A出发照到镜面OC上再反射到B的路线.对称点A′是A在镜面OC背后所成的虚像.从A′到B的直线距离等于折线段APB的总长度,也就是折线段的最短长度.
填空第9题与第5题类似,只不过现在有两面镜子OM,ON,同一个P在两面镜子背后各有一个虚像P1,P2,△PAB的最短周长等于虚像A1到A2的最短距离|P1P2|,PABP就是光从P出发经过两面镜子反射回到P的路线.
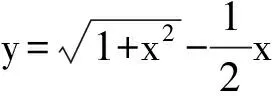
(提示:将y看成已知数,函数式看成以x为未知数的方程,求方程有实数解的条件.)
解将y看成已知数,函数式看成以x为未知数的方程.使方程有解的y值的集合就是函数f的值域,从中可以找到y的最小值.
这是x的一元二次方程,有实数解的条件为判别式
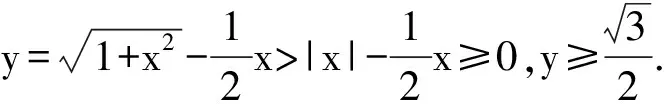
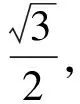
此时一元二次方程
取最小值.
题11蜜蜂的蜂巢的每个蜂房的形状可以由正六棱柱按如下方式得到:设O,O′分别是棱柱两个底面正六边形ABCDEF与A′B′C′D′E′F′的中心.在O′O的延长线上取点Q,过Q与A,C,E中每两个点作平面,得到3个平面QAC,QCE,QEA,分别交侧棱BB′,DD′,FF′于G,J,K,得到3个全等的菱形QAGC,QAKE,QCJE.在OO′的延长线上截取O′Q′=OQ,过Q′与A′,C′,E′中的每两点作平面可得到与前述三个菱形全等的三个菱形Q′A′G′C′,Q′A′K′E′,Q′C′J′E′.这六个全等的菱形与正六棱柱的各侧面围成一个蜂房,体积与原来的正六棱柱相同.选择点Q的位置使蜂房表面积最小,菱形的角α=∠AQC应是多大?
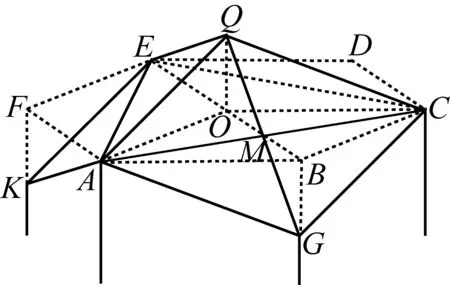
图4
解以底面正六边形的边长|AB|为长度单位1.正六棱柱侧面积为S0.设|BG|=x.则6个菱形与原来的侧面围成的蜂房表面积S等于S0减去侧面被切掉的与△ABG全等的12个三角形面积,再加上与菱形AQCG全等的6个菱形面积.
SAQCG=|AC||MG|
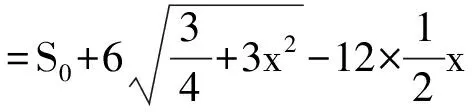
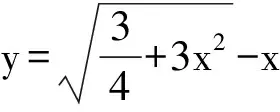
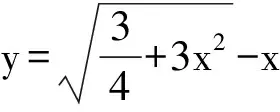
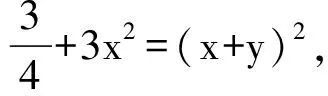
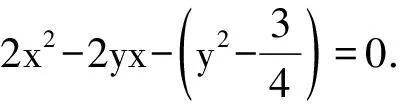
有实数解条件为
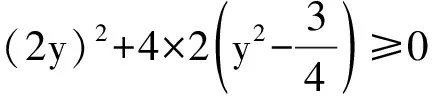
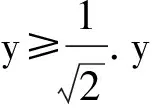
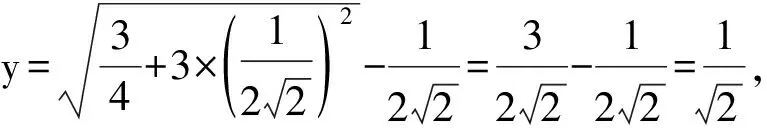
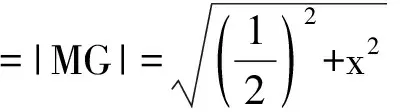
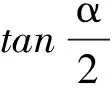
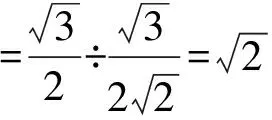
点评:生物学家实际测量了蜂房中这些菱形的内角,发现菱形的锐角都是70°32′,钝角都是109°28′.生物学家怀疑:按照这样的角度造出来的蜂房有可能是面积最小、最省材料的.生物学家请数学家帮助解决这个问题.一位数学家经过计算得到答案:要使表面积最小,菱形的锐角应当是70°34′.过了两年,另一个数学家重新算了一次,发现正确的答案就是70°32′.蜜蜂一分不差,数学家差了2′.不是数学家水平不够,而是因为他用的三角函数表精确度不够,导致了这2′的误差.
题7在有理数范围内分解因式:x15-1=_____________________________
解x15-1=(x5-1)(x10+x5+1)
=(x-1)(x4+x3+x2+x+1)(x10+x5+1)
(1)
x10+x5+1=(x10-x)+(x5-x2)+(x+x2+1)
=x(x9-1)+x2(x3-1)+x2+x+1
=(x3-1)[x(x6+x3+1)+x2]+x2+x+1
=(x2+x+1)[(x-1)(x7+x4+x2+x)+1]
=(x2+x+1)(x8-x7+x5-x4+x3-x+1).
答案:(x-1)(x4+x3+x2+x+1)(x2+x+1)(x8-x7+x5-x4+x3-x+1)
点评:怎么知道x2+x+1是x10+x5+1的因式?x2+x+1是x15-1的因式x3-1的因式,就应该出现在x15-1的因式分解中.但它在分解式(1)的三个因式中没有出现,就说明这三个因式没有分解到底,其中某个因式再分解就会出现x2+x+1.前两个因式x-1,x4+x3+x2+x+1都不被x2+x+1整除,唯一的可能是最后一个因式x10+x5+1被它整除.
可以强行用x10+x5+1除以x2+x+1.另一个办法是x10+x5+1先除以x3-1求余式,再用余式除以x2+x+1.x3=(x3-1)+1除以x3-1的余式等于1.将x3替换成1,除以x3-1的余式不变.将x10+x5+1=(x3)3x+x3x2+1中的x3都替换成1,得到余式x+x2+1.将x10+x5+1减去这个余式x+x2+1,得到的
x10-x+x5-x2=x(x9-1)+x2(x3-1)
可以提取公因式x3-1进而提取公因式x2+x+1,得到以上解法.
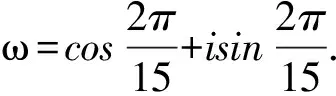
x15-1=(x-1)(x-ω)(x-ω2)…(x-ω14).
求证:x15-1的如下因式都是整系数多项式:
f1(x)=(x-ω5)(x-ω10),
f2(x)=(x-ω3)(x-ω6)(x-ω9)(x-ω12),
f3(x)=(x-ω)(x-ω2)(x-ω4)(x-ω7)(x-ω8)·(x-ω11)(x-ω13)(x-ω14).
解当m为整数时(ω5m)3=(ω15)m=1m=1.ω5m是方程x3-1=0的根.取m=1,2得ω5,ω10是方程x3-1=0的两个不同的根,另一个根是1.因此x3-1=(x-1)(x-ω5)(x-ω10).
是整系数多项式.
当m是正整数时,(ω3m)5=(ω15)m=1,ω3m是方程x5-1=0的根.取m=1,2,3,4得到1以外的4个不同的根ω3,ω6,ω9,ω12.因此
x5-1=(x-1)(x-ω3)(x-ω6)(x-ω9)·(x-ω12),
是整系数多项式.
x15-1=(x-1)(x-ω)…(x-ω14)是15个一次因式x-ωk(k=0,1,2,…,14)的乘积.其中k=0的一次因式x-1系数是整数.
k=5m(m=1,2)的两个一次因子的乘积(x-ω5)(x-ω10)=f1(x)系数都是整数.
k=3m(m=1,2,3,4)的4个一次因子的乘积(x-ω3)(x-ω6)(x-ω9)(x-ω12)=f2(x).
除此之外所有的一次因子的乘积
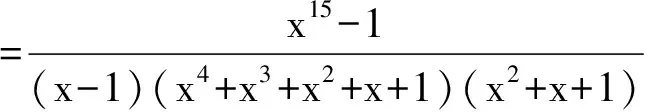
=x8-x7+x5-x4+x3-x+1.
借题发挥:分圆多项式
第10题用另一种方式在有理数范围内对x15-1作了因式分解:
x15-1=(x-1)f1(x)f2(x)f3(x)
=(x-1)(x2+x+1)(x4+x3+x2+x+1)(x8-x7+x5-x4+x3-x+1).
分解的方法是:先在复数范围内彻底将x15-1分解为一次因子x-ωk(0≤k≤14)的乘积,其中每个根ωk满足x15=1,都是1的15次方根,称为15次单位根.并且存在最小正整数d使(ωk)d=1,称ωk为d次本原单位根.d是15的因子,只能为1,3,5,15.以全体d次本原单位根为根的多项式是整系数多项式,记作Φd(x),称为分圆多项式.
Φ1(x)=x-1,Φ3(x)=x2+x+1,
Φ5(x)=x4+x3+x2+x+1,
Φ15(x)=x8-x7+x5-x4+x3-x+1.
x15-1=Φ1(x)Φ3(x)Φ5(x)Φ15(x)被分解为各个分圆多项式Φd(x)的乘积,d=1,3,5,15取遍15的所有因子.
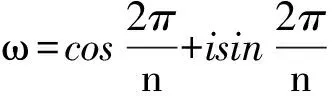
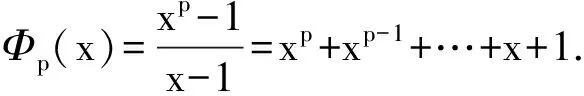
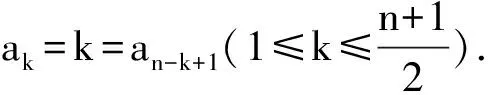
(提示:考虑向量a1(cosα,sinα)+…+an(cosnα,sinnα)的方向.)
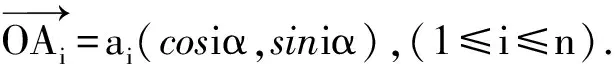
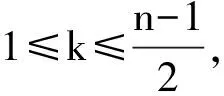
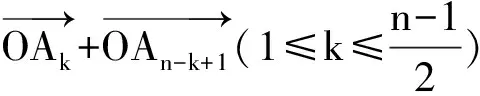
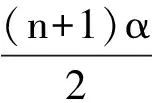
题13圆柱底面半径为r.用一个平面斜截圆柱的侧面,截得的侧面的最大高度为a,最小高度为b,a>b>0.
(1)试画出截得侧面的展开图(只须画出简图即可).猜测截痕展开得到的曲线是什么形状的曲线.
(2)在适当坐标系下求截痕展开所得曲线的方程.这是什么曲线?
解(1)侧面展开如图6.截痕展开曲线看起来是余弦函数图象,也是正弦函数图象.
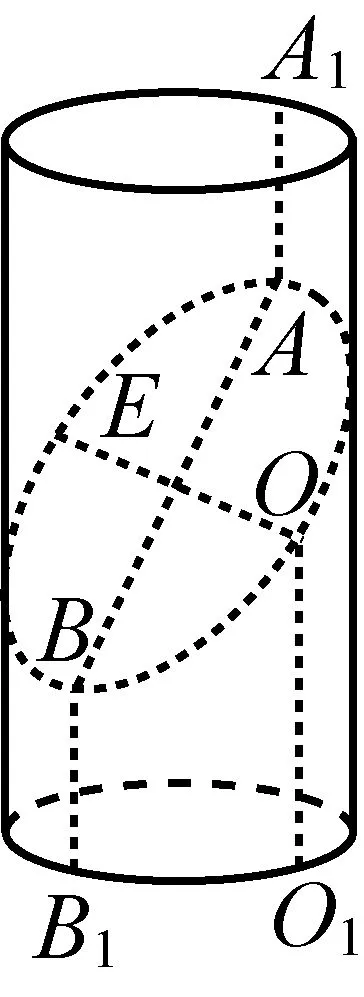
图5
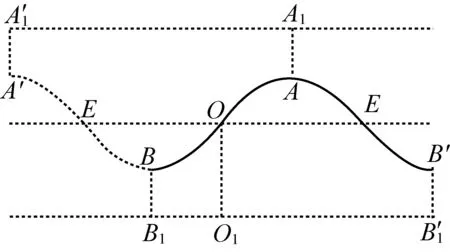
图6
点评:题目不要求画图精确,却要求反映曲线的主要特征.
2.对称:不妨设图5中|AA1|=|BB1|,斜截面上半段圆柱绕OE旋转180°之后与下半段重合.因此,图6的O点右上方曲线段OA绕O旋转180°与OB重合,EA绕E旋转180°与EB′重合.
(2)如图7,圆柱两个底面圆心的连线l是侧面的对称轴.设C是斜截面与对称轴的交点.过C作平面垂直于对称轴l,称为圆柱的直截面,它与圆柱侧面的交线是以C为圆心、半径为r的圆,与斜截面的交线是这个圆的一条直径OE.以C为原点,CO为x轴正方向,下底面圆心到上底面圆心的方向为z轴正方向建立空间直角坐标系.
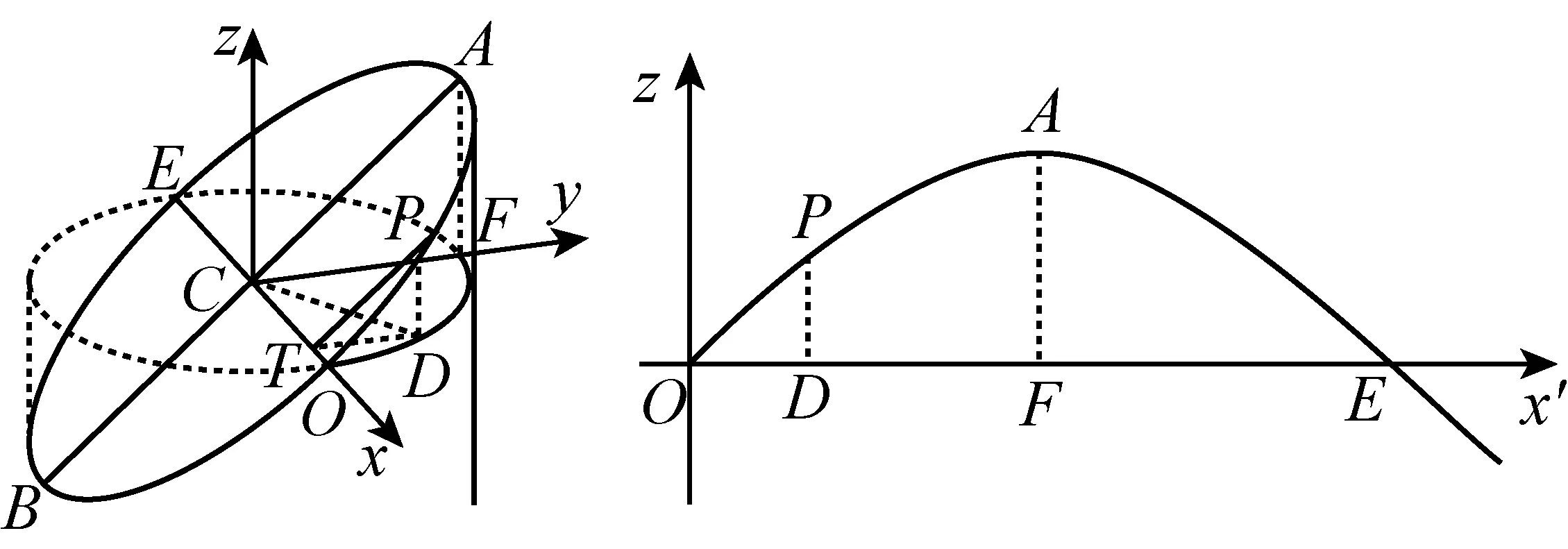
图7
圆柱侧面在Cxy平面上的投影是以C为圆心的圆x2+y2=r2,圆柱侧面上所有点(x,y,z)的坐标都满足此方程,z坐标不受限制.
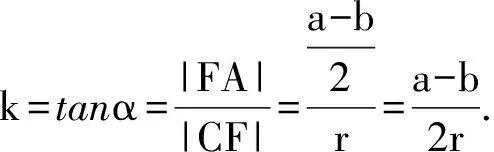
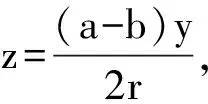
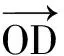
因此截痕展开后的曲线在适当的坐标系中是正弦函数的图象.
点评:最早出这个考题时,高中数学没讲空间坐标,只能用立体几何方法求截痕展开曲线上点P(x′,z)的坐标.横坐标x=OD是直截面圆周上一段弧长,纵坐标z=DP是斜截面上的点P到直截面的距离.在直截面上作DT⊥CO得到斜截面与直截面所成二面角的平面角α=∠DTP,可以在直角三角形TDP和CFA中算出
这就需要更强的空间想象能力才能做出来.
现在高中学了空间坐标,虽然没有学圆柱侧面的方程,但可以将侧面投影到直截面(Cxy坐标面)变成圆,写出圆方程x2+y2=r2.这个方程在平面上的图象是圆,空间中的点(x,y,z)只要投影在这个圆上,x,y坐标就满足方程,不论z坐标怎么变化,都在这个方程的图象中.因此方程的图象是以这个圆为直截面的圆柱面.类似地,斜截面在Cyz面上的投影是过原点的直线,方程形式为z=ky,投影到这条直线上的所有点(x,y,ky)都在方程图象中,图象是过直线z=ky所作的与Cyz垂直的整个平面.利用平面直线和圆方程的旧知识,得出空间的圆柱面和平面方程来解决新问题,体现的是数学建模核心素养.
题15空间中同一点出发两两成钝角的射线最多几条?并说明理由.
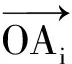
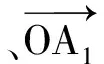
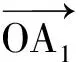
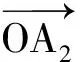
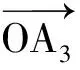
如果n≥5,则z4与z5都与z3异号,因而z4,z5同号,
=(-|x4|,-|y4|,z4)·(-|x5|,-|y5|,z5)
=|x4||x5|+|y4|y5|+z4z5>0,
矛盾.这迫使n≤4.
存在4个向量两两成钝角.例如(1,0,0),(-1,1,0),(-1,-2,1),(-1,-2,-6).因此,空间中从一点出发两两成钝角的射线最多4条.
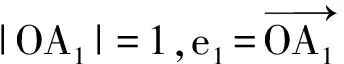
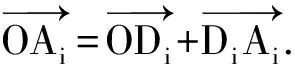
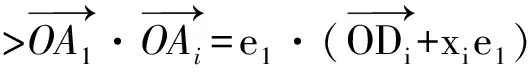
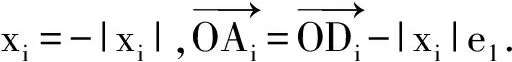
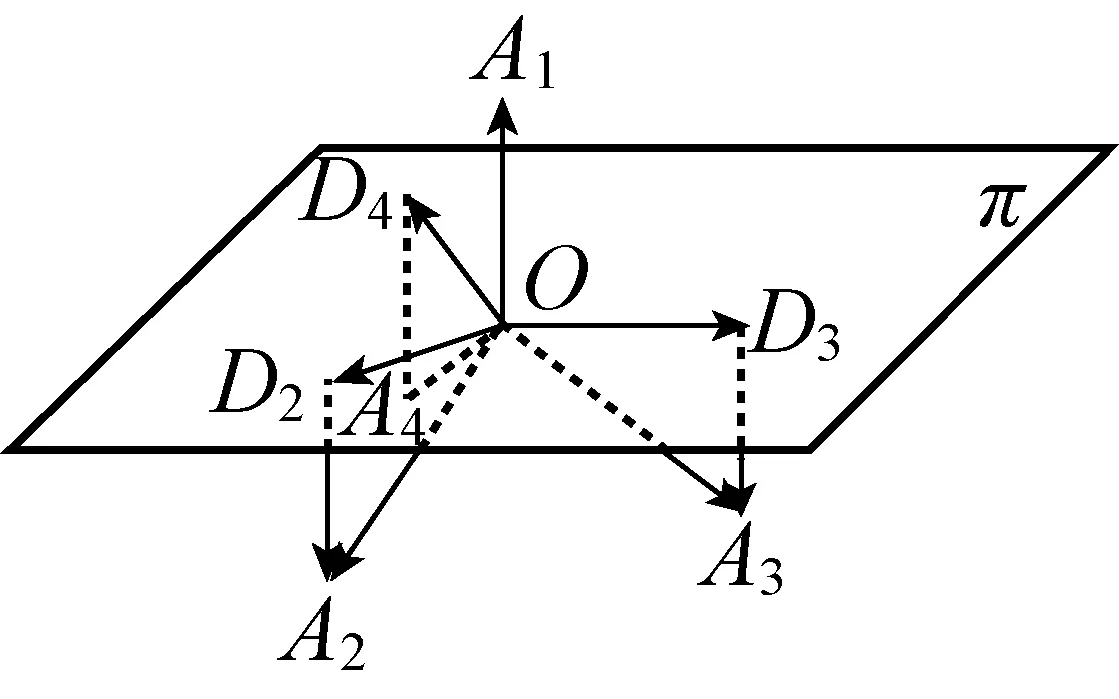
图8
对任意j>i≥2,有
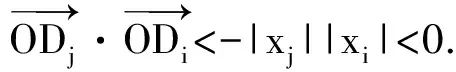
这证明了OA2,…,OAn在平面π上的投影OD2,…,ODn两两内积为负,夹角大于90°.从OD2开始将这些投影线段ODi按逆时针旋转顺序排列为OD2,ODi3,ODi4,…,ODin,OD2,其中相邻线段夹角∠DikODik+1>90°,因而
360°=∠D2ODi3+∠Di3ODi4+…+
∠DinOD2>(n-1)90°
⟹4>n-1⟹5>n⟺n≤4.
另一方面,存在4个两两成钝角的非零向量.如图9.
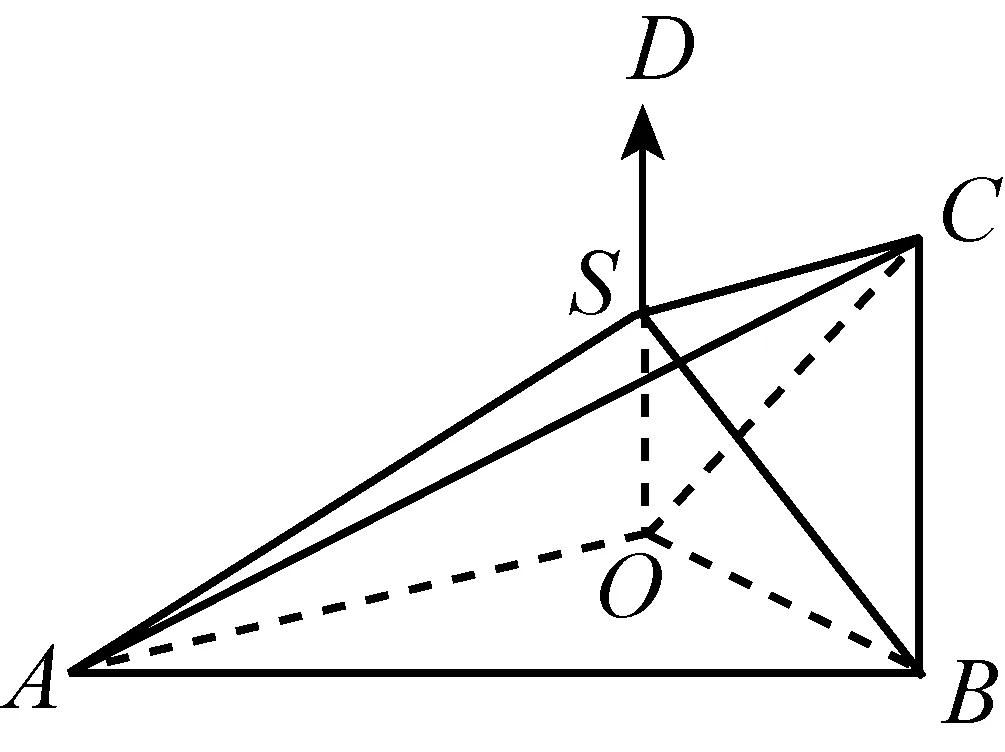
图9
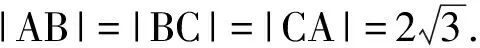
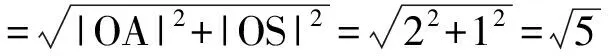
=|SB|=|SC|.
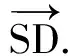
这证明了:空间中从同一点出发两两成钝角的射线最多有4条.(全文完)
