代数几何相转化 相映成辉是一家——对一道高考圆锥曲线问题的变式探究

范方兵 王芝平

(1.北京市第二中学 100010 2.北京宏志中学 100013)

试题再现：已知抛物线C:y2=2px经过点P(1，2).过点Q(0，1)的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N.

(Ⅰ)求直线l的斜率的取值范围；

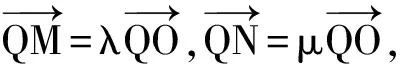
这是2018年高考北京卷理科的第19题，在全卷中处于倒数第二题的位置，题目设计新颖，背景深刻，难度适中，以抛物线为载体考查直线与圆锥曲线的位置关系，考查解析几何的坐标化思想、数形结合、化归转化思想以及数学运算、逻辑推理等核心素养，是一道值得细细品味的好题.现将本题的解答及分析过程整理如下，希望得到同行的指教.

1 试题解法变式研究

解(Ⅰ)由题意，C:y2=2px经过点P(1，2)，所以22=2p×1，所以2p=4，抛物线C:y2=4x.

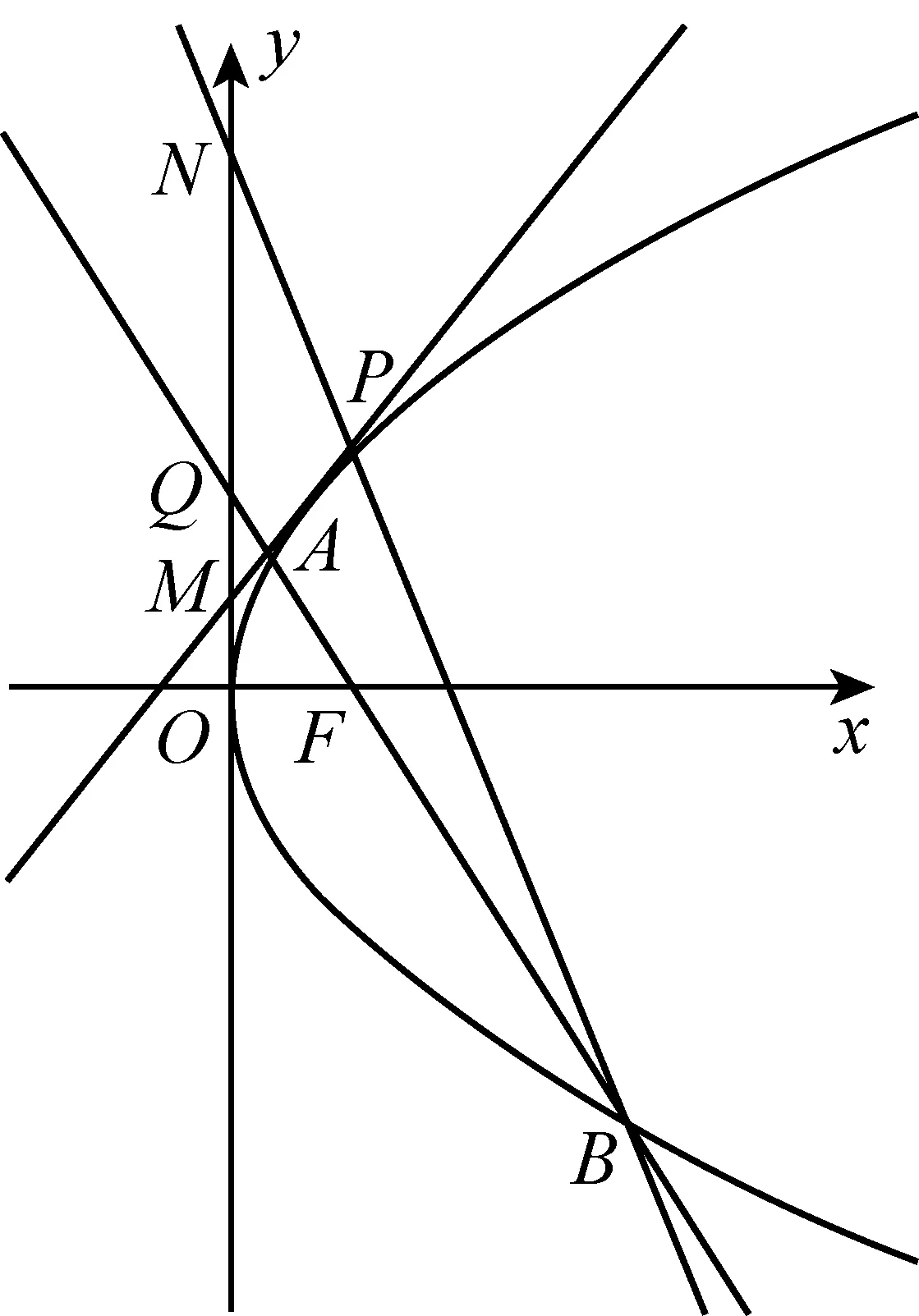
图1

易知直线l的斜率存在，设其方程为y=kx+1(k≠0)，与抛物线C:y2=4x联立得：

k2x2+(2k-4)x+1

=0，

由题意有，k≠0且Δ=16-16k>0，得k<1且k≠0.

如图1，PB与y轴有交点，故点B不能是点P(1，2)关于x轴的对称点(1，-2)，故k≠-3.

所以k的取值范围为

(-∞，-3)∪( -3，0)∪(0，1).

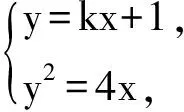
整理得ky2-4y+4=0.

设A(x1，y1)，B(x2，y2)，

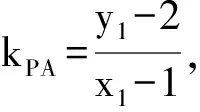
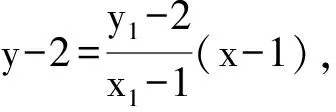
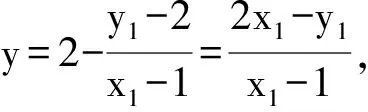
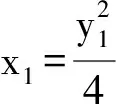
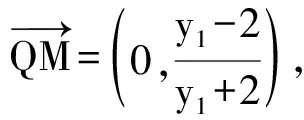
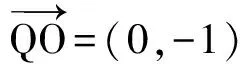
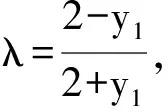
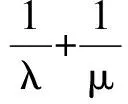
解法二设A(x1,y1),B(x2,y2),M(0,yM),N(0,yN)，

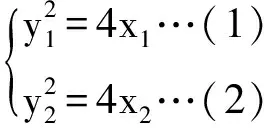
由Q,A,B三点共线知x1(y2-1)=x2(y1-1)，

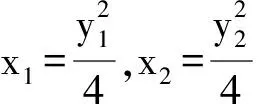
整理得y1y2=y1+y2…(3)

由P,A,M三点共线知

(x1-1)(yM-2)=-(y1-2)，

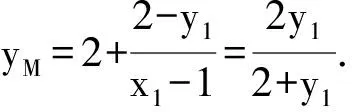
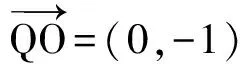
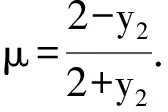
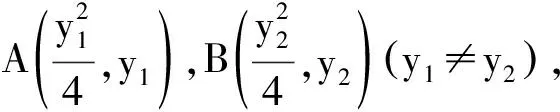
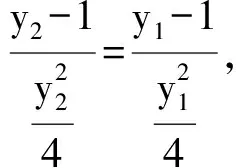
整理得y1y2=y1+y2.

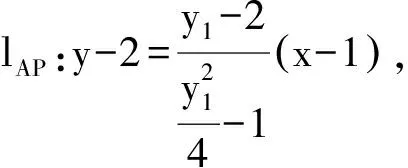
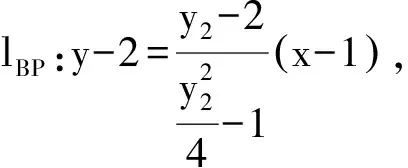
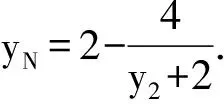
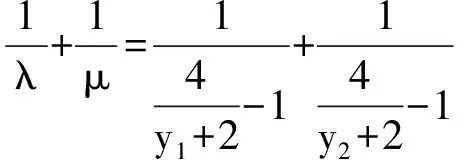
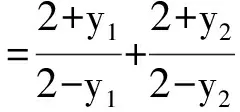
2 试题变式及探源

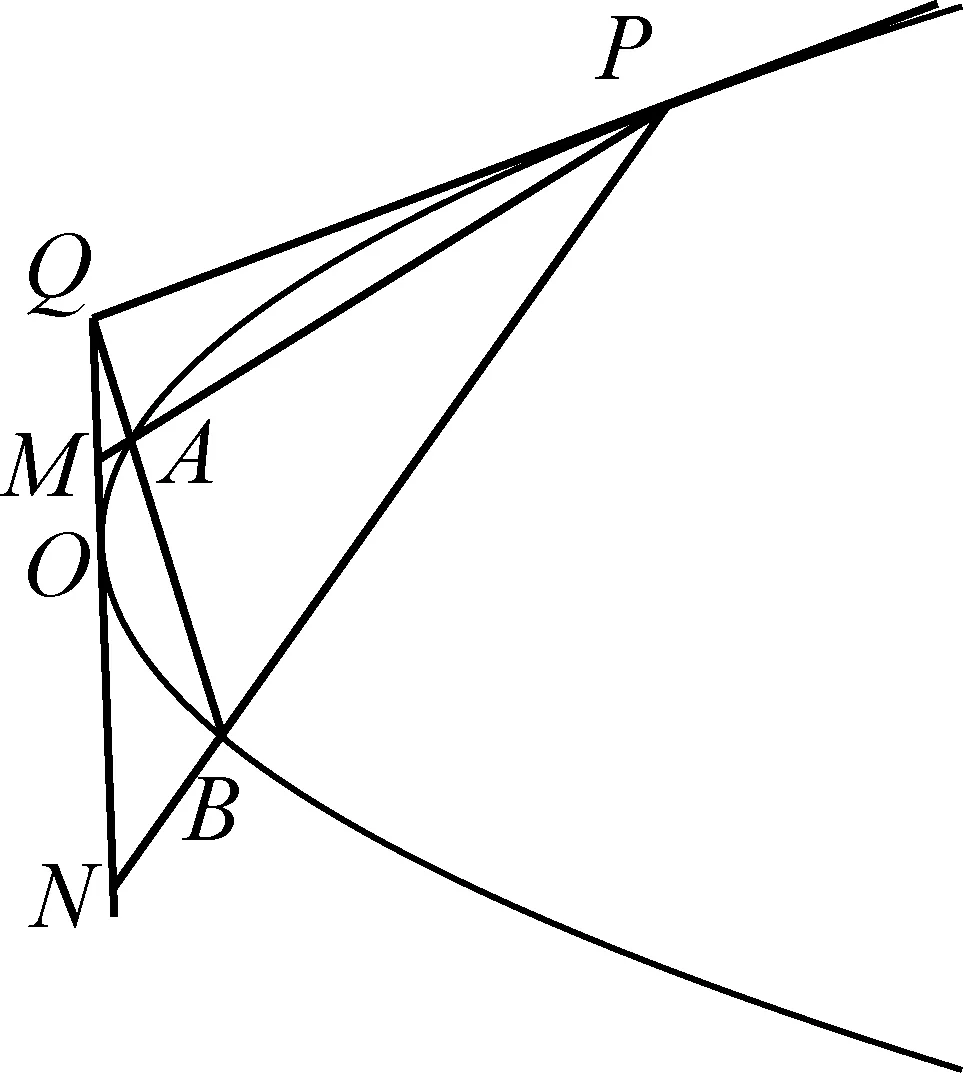
图2

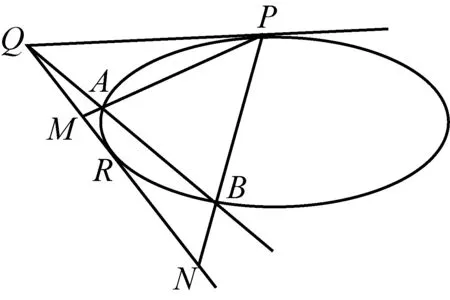
图3

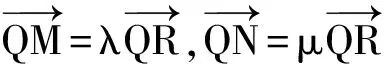
实际上，本文所探讨的题目以及猜想，与2008年高考安徽卷理科数学第22题有着内在联系，其几何背景涉及到高等几何中的极点、极线以及调和点列的知识，现逐步来进行说明(关于极点、极线的知识，限于篇幅暂不做深入探讨).

(Ⅰ)求椭圆C的方程；

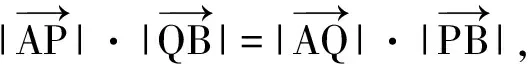
一方面，本文第二作者在文[1]对这道题目作了一般化的证明，并在此基础上进行了变式推广，使得结论更加丰富，内容更加精彩.文中得到了如下的命题及推论：

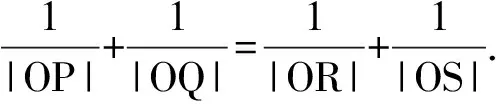
特别地，当直线l过直线AC与BD的交点，即P与Q重合时有如下的推论：

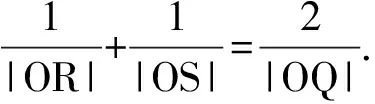
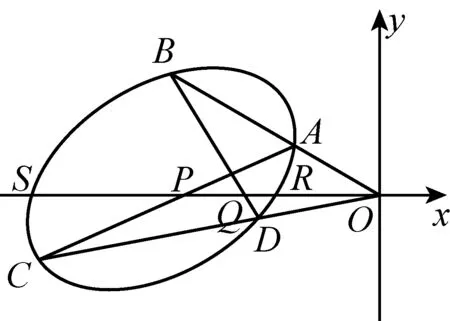
图4

当A与B、C与D分别重合于一点时，有：

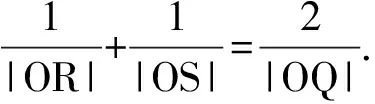
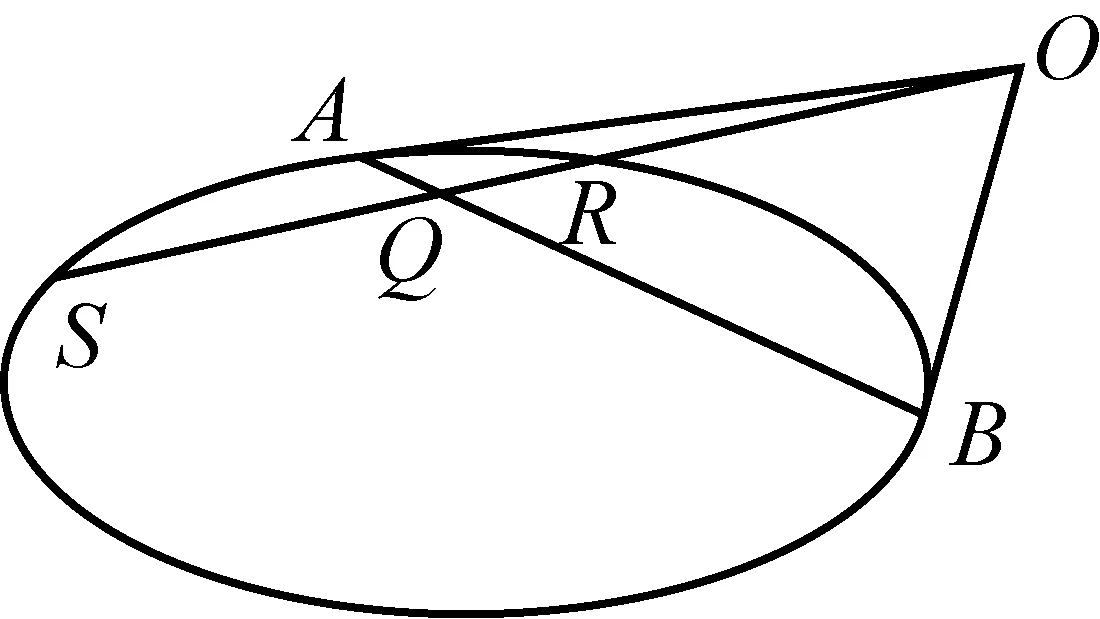
图5

另一方面，上述谈到的调和点列，是研究图形在射影变换下不变性的一个几何学分支，简单地说，经过有限次两平面间的中心投影(透视)得到的平面上的一一点变换，称为平面上的射影变换.其产生的最初动力，是为了帮助绘画而对透视进行的研究.在17世纪，G.德扎格和B.帕斯卡建立了射影几何学中的著名定理，后来在19世纪，又经过J.V.彭赛列、J.施泰纳、A.F.麦比乌斯等几何学家的工作，使射影几何学得到蓬勃的发展，达到鼎盛时期.

定义一调和点列

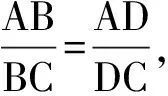
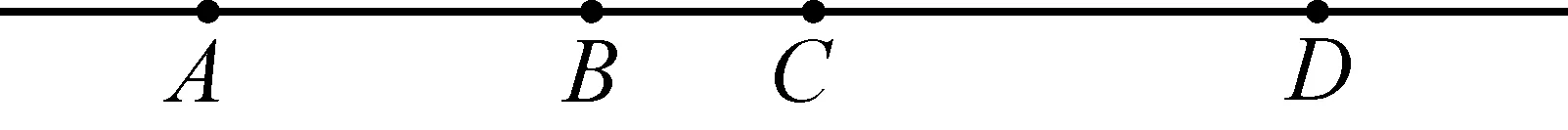
图6

性质如果A,B,C,D是调和点列，则

事实上，由A,B,C,D是调和点列可知

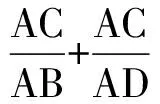
定义二调和线束

过调和点列A,B,C,D所在直线外一点P，向A,B,C,D引四条线束(射线)，称这四条线束为调和线束.

性质如图7，设与调和线束相交于四点的直线l′与其交于A′,B′,C′,D′，则点A′,B′,C′,D′也为调和点列.

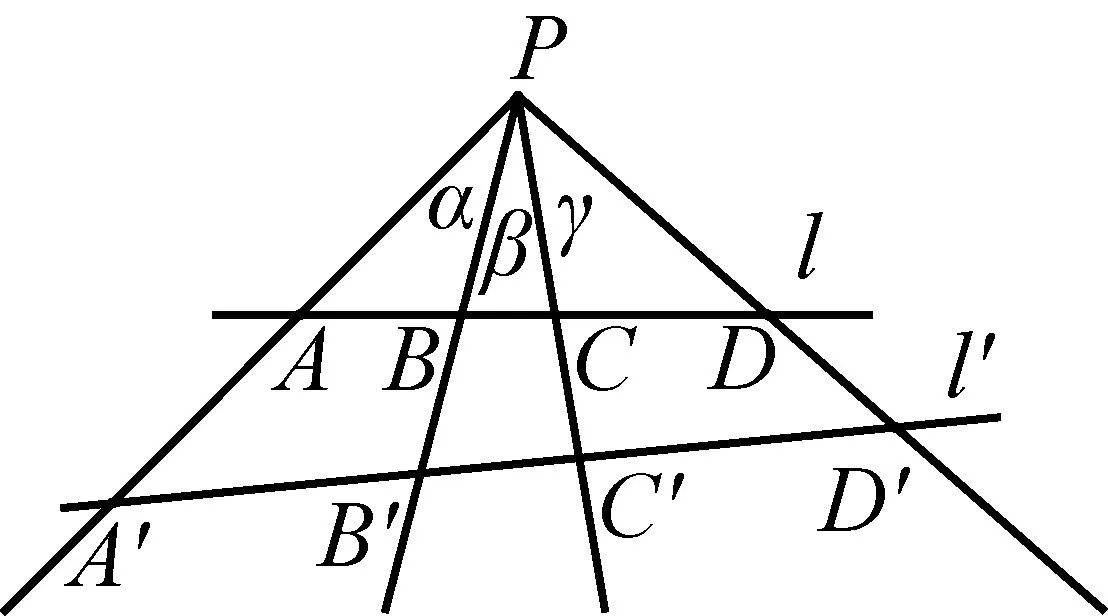
图7

事实上，由A,B,C,D是调和点列可知

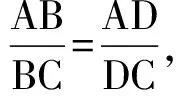
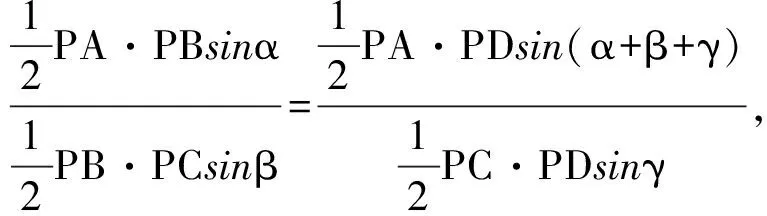
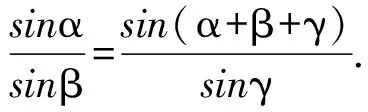
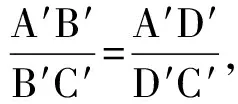
有了上面的讨论，如图8，作出射线BR,BS，分别与直线OA交于M,N，如图.

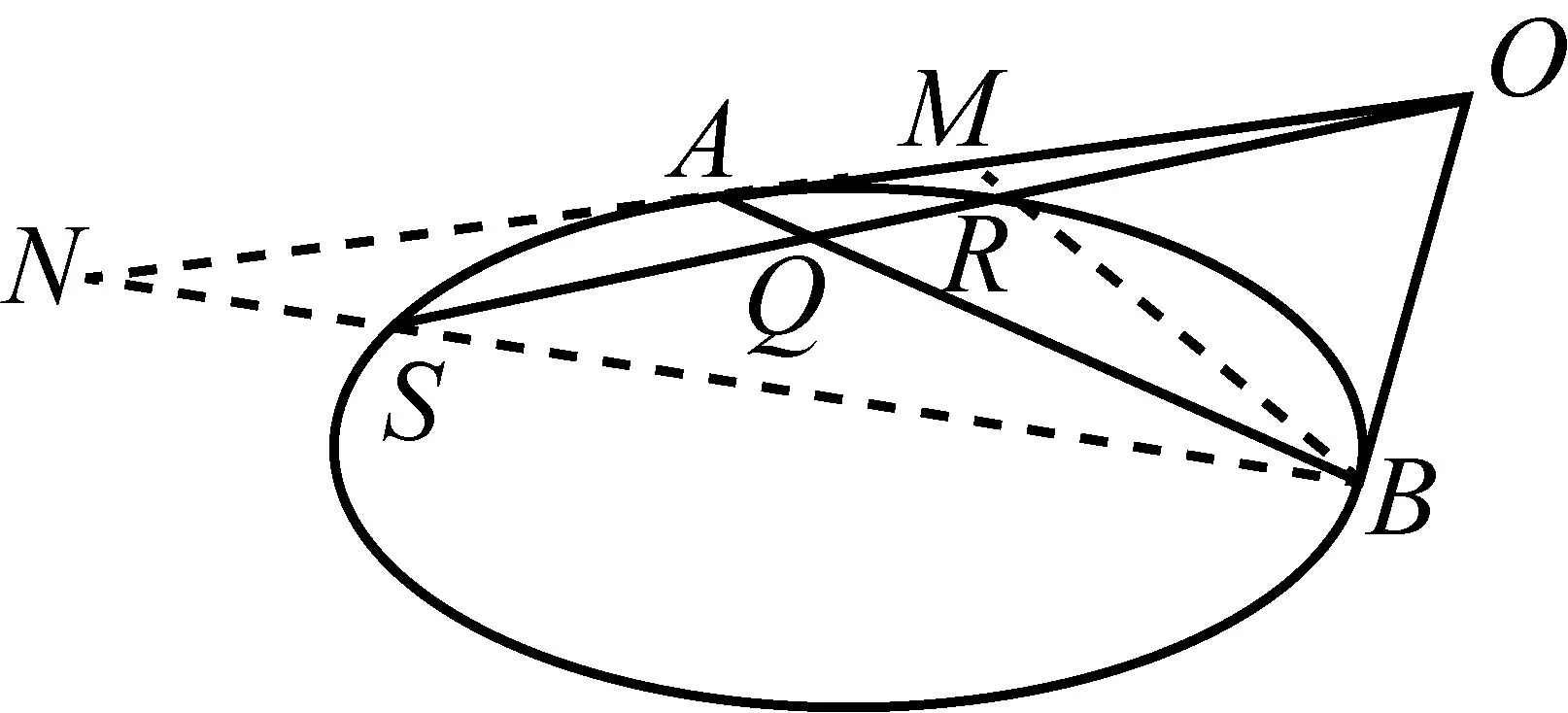
图8

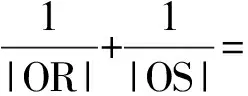
基于以上的分析，前面作出的猜想是正确的，这个结论非常精彩：一方面，这个结论渗透了运动变化的观点，并且揭示了运动变化中不变的规律；另一方面，这个结论也说明2018北京高考解析几何题的几何背景非常深刻，有着广泛的实际应用，对“解析几何其实质是平面几何”作了一个好的注解；进而，通过对问题的探讨，让我们认识到，如果只是利用纯粹的平面几何知识去进行推理、演算，有时显得十分复杂，而在引进平面直角坐标系，将平面几何问题转化为一个代数问题后，利用代数方法也可以解决平面几何问题，这不仅仅是多了一种方法，有时更能体现代数方法的优越性，体现解析几何的学科价值.

一个好的数学结果，除了问题本身漂亮外，还应该具有推广的潜力，是许多相关结果中的交汇点．本试题就具有这样的推广潜力，它还有很多有趣的性质等待人们去探索．

正所谓：代数几何相转化，相映成辉是一家．