对三角形中一种综合置换方式的几何解释
2018-08-30付相兵孟凡海
数学通报 2018年7期
贺 斌 付相兵 孟凡海
(湖北省谷城县第三中学 441700)
贵刊文[1]通过一个多版面的篇幅证明了如下命题
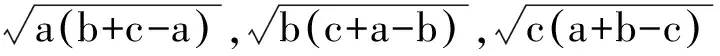
并在此基础上建立了如下置换:
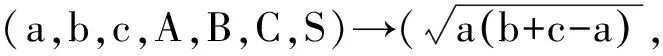
文[1]的证明条理清楚,逻辑严谨,但其缺点是不够直观.本文(仍沿用文[1]的相关记号)将给出上述命题的一个几何解释,并在此基础上建立一个可以将涉及三角形边长、面积及相关半径的齐次关系式转化为仅含角的三角函数的关系式的置换.
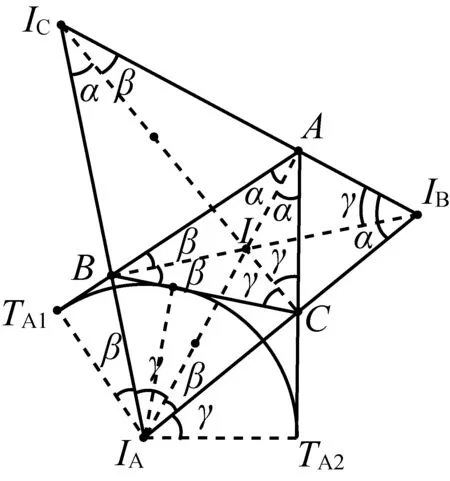
图1

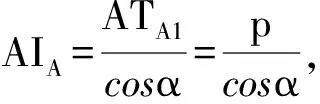
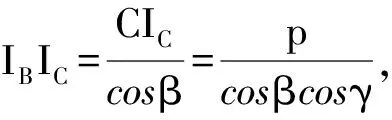
所以面积为
设△ABC的内切圆半径为r,
则r=(p-a)tanα=(p-b)tanβ=(p-c)tanγ,
所以,r3=(p-a)(p-b)(p-c)·tanαtanβtanγ=r2ptanαtanβtanγ,
所以r=ptanαtanβtanγ,
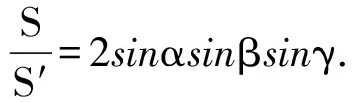
这样我们便得文[1]命题的几何解释.
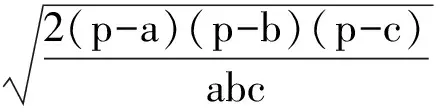

(相关字母的意义如前所述)
利用此置换可以将涉及三角形边长、面积及相关半径的齐次关系式转化为仅含角的三角函数的关系式.读者不妨一试.
