顺势拓展 追问导学——基于一节《函数零点问题的数形结合分析》课例的分析

福建省龙岩第一中学 (364000) 庄炯林

众所周知，一个成功的教育者，绝非照本宣科、生搬硬套地填鸭式教学就能够成就的.传授知识不是在建图书馆，否则建一所学校只要建图书馆和配备相应的管理员就行了，教师岂不是无足轻重可有可无？恰恰，教师在教学中要充当思想领袖、是智慧的集大成者，教师传授给学生的学习方法、思考方式比传授知识本身更重要.题目千变万化，做不完，但是题型却有固定的路数.在教师平时的教学过程中，不能一味地追求题海题量，而应该要能在一道道经典的题目当中擅长挖掘、拓展、延伸、逆向分析，那么，这一道题目便是千千万万的题目的化身，达到真正以学生为本、教师是主导，学生是主体的高效课堂目标.下面就以“追问导学”方式对生成知识与方法做一次课堂教学探讨.

一、教学内容分析

初学者(高一学生)大多不清楚为什么要研究函数的零点，因为在此之前他们都能用公式法直接求方程的根．其实，函数的零点问题是中学数学的一个重要概念,从函数值与自变量对应的角度看,就是使函数值为0的实数x.从方程的角度看,即为相应方程的实数根；从函数的图像角度看,函数的零点就是函数与x轴交点的横坐标.对于高中所接触的函数相对较为复杂，除了研究函数的零点个数，还涉及到含参数的零点问题、复合函数的零点问题等等，教学时可通过举例让学生知道，有许多方程都不能用公式法求解，只能把方程交给函数，转化为考察相应函数的零点问题，从动态的角度来研究，以静制动，借助形的角度来研究数的问题．所以函数的零点从不同的角度,将函数与方程，数与形有机的联系在一起，体现的是函数知识的应用.

二、教学实录片段

1.提出问题，揭示方法

引例已知函数f(x)=

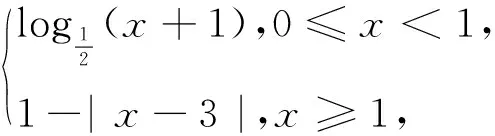
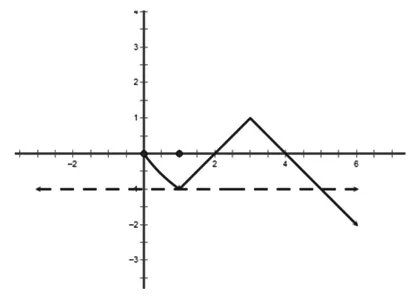
图1

分析：首先可用函数与方程思想，将“函数y=f(x)-a存在三个零点”转化为“方程f(x)-a=0存在三个解”即“函数y=f(x)与函数y=a有三个交点”，最后用数形结合思想分析.如图1所示，当a∈(-1,0]时，函数y=f(x)与函数y=a有三个交点.

设计意图：让学生初步掌握数形结合思想在零点问题的应用.从讨论方程的解(或函数的零点)的个数问题揭示方法，将问题转化为讨论两曲线的交点个数,其基本步骤是先把方程两边的代数式看作是两个熟悉函数的表达式(不熟悉时,需要作适当变形转化为两个熟悉的函数),然后在同一坐标系中作出两个函数的图像,图像的交点个数即为方程解(或函数零点)的个数.

2.顺势拓展，追问深化

追问1：已知函数f(x)=

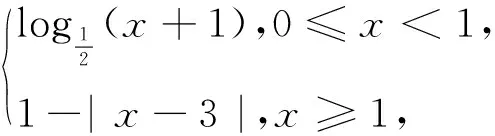
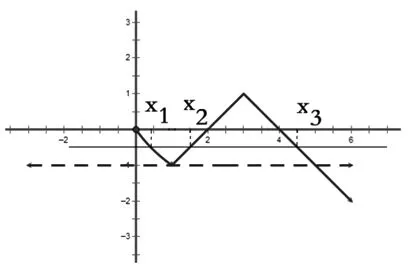
图2

生1：根据刚才引例的分析，如图2所示，当a∈(-1,0]时，函数y=f(x)与函数y=a有三个交点，且在直线y=a平移中x2,x3始终关于x=3对称，即x2+x3=6，又x1∈[0,1)，所以x1+x2+x3=x1+6∈[6,7).

师：对，生1能利用刚才现有的成果进一步分析，使得问题得以解决.那同学们再看.

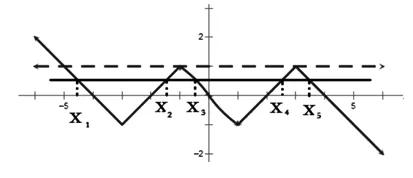
图3

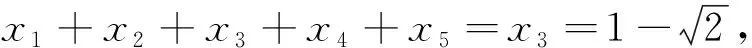
师：不错！生2不仅能利用函数的奇偶性将函数图像补全，而且利用奇偶性求解函数解析式，从动态图形的观察，以静制动的方式实现问题的解答.接下来，同学们再看.

取M>max{2,2p,1+p}, 可知 由引理1.3、马尔可夫不等式、 p≥1、E|X|1+p<∞、条件(A1)和式(2.4)得

A．5B．6C．7D．8

图4

生3：“函数y=[f(x)]2+f(x)的零点个数”等价于“方程[f(x)]2+f(x)=0根的个数”，令t=f(x)则t2+t=0，得t=0或t=-1，此时f(x)=0及f(x)=-1的解为方程[f(x)]2+f(x)=0根的个数，即函数y=[f(x)]2+f(x)的零点个数.如图4所示，函数y=f(x)与y=0有5个交点，函数y=f(x)与y=-1有3个交点，共8个，故选D.

师：对！追问3带来复合函数的零点问题，生3巧妙的利用换元法，转化为内函数与外函数的零点问题，赞！如果是接下来这题呢？

生4：以生3的解题提示，令t=f(x)，则t2+at+2a=0，如图5-1所示，函数y=f(x)与y=t在t∈(-1,1)内有5个交点，也是最多交点，要使得方程[f(x)]2+af(x)+2a=0有10个不相等的根，方程t2+at+2a=0在t∈(-1,1)内须有不同的两解，即函数g(x)=t2+at+2a在(-1,1)有两个不同的零点，如图5-2所示，有

图5-1 图5-2

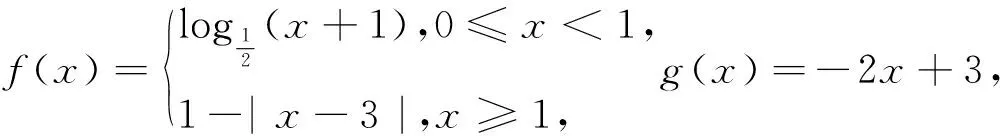
A.方程f(f(x))=0有且仅有3个根

B.方程g(g(x))=0有且仅有4个根

C.方程g(f(x))=0有且仅有5个根

D.方程f(g(x))=0有且仅有6个根

图6-1 图6-2

生5：如图6-1所示，A选项中，满足方程f[f(x)]=0的f(x)有3个不同的值，f(x)等于-2，0，2，而当f(x)=0时对应3个不同的x值；当f(x)=±2时，没有对应的x值．故满足方程f[f(x)]=0的x值共有3个，即方程f[f(x)]=0有且仅有3个根，故A正确．

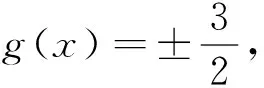
如图6-1、6-2所示，D选项中，满足方程f[g(x)]=0的g(x)有三个不同值，g(x)等于-2，0，2，如图可知，由于每个g(x)值对应了2个x值，故满足f[g(x)]=0的x值有6个，即方程f[g(x)]=0有且仅有6个根，故D正确．故选C.

师：非常好！生5能融会贯通，分别从两个函数图像中的零点个数出发，将多组合的复合函数一一分析清楚，利用数形结合思想解决问题，达到“不画图，没前途，画了图，不糊涂”的境界.

设计意图：让学生学会“学中思考，融会贯通”，提升素养.设计一个入口较宽的问题，顺势拓展问题，步步追问的形式，让每一个追问都有一定挑战性，让学生从一题多变中体会知识的连续性，让学生合理利用现学的理论知识求解，逐步拓宽解题思维，不仅培养学生数形结合的意识，也达到知识认知的广度和宽度.使学生能将陌生的问题转化为常规问题，把数的问题转化为形的问题，当依靠形说不清时再次把形的问题转化为数，感受数学解题其实就是一个不断转化的过程．

3.点拨指导，归纳总结

问题：以引例为出发点，顺势拓展步步追问，你有哪些收获？

设计意图：在学生谈收获，谈体验的过程中，教师将本节课的内容回顾总结，概括升华，进一步优化学生的认知结构，把课堂所学的知识与方法较快转化为学生的核心素养，也更进一步培养学生的归纳概括能力．主要是让学生归纳总结以下两点：①函数零点问题转换的方法与技巧；②数形结合思想应用的方针与策略.

三、教与学的思考

在课堂教学中让学生在亲身体验中认识数学思想方法，解决问题，理解和掌握基本的数学知识、技能和方法.多关注学生课堂学习的过程.以问题串组织教学，一步步引导学生自主建构思路，5个追问把整节课知识点串了起来，这样的课堂是高效的，学生在思考中发现，在探究中感悟．立足放手让学生来说，把舞台交给学生，充分体现教师为主导，学生为主体的教学理念．学生的大胆尝试，缜密的思维，条理清晰的思路正是我们老师希望看到的，这样的学生也是我们老师希望培养的．