三角形被切分成两个等腰三角形的条件及应用
2018-08-30广东省广州市第二中学510040郭旭彬
广东省广州市第二中学 (510040) 郭旭彬
等腰三角形是一类特殊的三角形,具有非常丰富的几何性质.一般情况下,若所讨论的问题涉及等腰三角形,并且题目没指明顶角或底角、腰或底边,则均需要进行讨论.图形的切分是构建几何问题的一种常见方法,例如根据直角三角形斜边中线的性质可知,任意直角三角形都可以被斜边中线切分成两个等腰三角形.但是通过具体的例子不难得出,并不是任何的钝角三角形或锐角三角形都可以被某条直线切分成两个等腰三角形的.在日常教学中,学生如果碰到把一个三角形切分成两个等腰三角形的问题,经常难以下手,或者很难正确地进行分类讨论,给问题解决造成一定困惑.本文想通过一些尝试,主要讨论一个三角形可以被切分成两个等腰三角形所需要满足的条件及其应用.
一、问题探索
若要把一个三角形切分成两个三角形,则切分的直线应该过某个顶点.如图1,已知AD把ΔABC分成两个等腰三角形ΔABD和ΔACD.下面分两种情况进行讨论:
1.当∠ADB=∠ADC时,如图2,因为∠ADB+∠ADC=180°,所以∠ADB=∠ADC=90°.又因为ΔABD和ΔACD为等腰三角形,所以BD=DA=DC.所以∠BAD=∠CAD=45°,即∠BAC=90°.此时ΔABC满足的条件是:ΔABC中含有一个角等于90°.
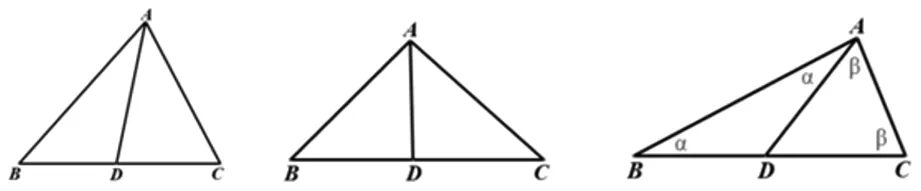
图1 图2 图3
2.当∠ADB≠∠ADC时,不妨设∠ADB>∠ADC:因为∠ADB>∠ADC且∠ADB+∠ADC=180°,所以∠ADB>90°,∠ADC<90°.又因为ΔABD和ΔACD为等腰三角形,且钝角不可能为等腰三角形的底角,所以BD=AD.设∠B=∠BAD=α.
(1)若∠ADC为等腰三角形的顶角,则DA=DC,如图3,设∠C=∠DAC=β,则∠BAC=α+β.
由∠BAC+∠B+∠C=180°可得α+α+β+β=180°,即∠BAC=α+β=90°.此时ΔABC满足的条件是ΔABC中含有一个角等于90°.
(2)若∠ADC为等腰三角形的底角,并且∠ACD也是等腰三角形的底角时,如图4,由∠ADC=∠B+∠BAD,可得∠ADC=∠ACD=2α,设∠CAD=β,则由∠BAC+∠B+∠C=180°可得α+β+α+2α=180°.
因为β>0,所以0°<4α<180°,即0°<α<45°.故ΔABC满足的条件是ΔABC的三个角大小为α,2α,180°-3α且0°<α<45°.

图4 图5
(3)若∠ADC为等腰三角形的底角,并且∠CAD也是等腰三角形的底角时,如图5,由∠ADC=∠B+∠BAD,可得∠ADC=∠CAD=2α.
设∠ACD=β,则由∠BAC+∠B+∠C=180°可得α+2α+α+β=180°.因为β>0,所以0°<4α<180°,即0°<α<45°.故ΔABC满足的条件是ΔABC的三个角大小为α,3α,180°-4α且0°<α<45°.综上所述,当ΔABC满足下列条件之一时,ΔABC可以被切分为两个等腰三角形:
(1)当ΔABC有一个内角等于90°时,切分方式如图3;
(2)当ΔABC的三个内角大小为α,2α,180°-3α且0°<α<45°时,切分方式如图4;
(3)当ΔABC的三个内角大小为α,3α,180°-4α且0°<α<45°时,切分方式如图5.
二、实例应用
根据上述讨论,当且仅当一个三角形的三个内角满足上述三个条件之一时,它才能被一条直线切分成两个等腰三角形.当我们遇到此类问题时,可以按照这三个条件对三角形三个内角所要满足的要求进行分类讨论.下面结合三个常见的问题说明在实际解题中如何应用.
问题1 一个三角形可被剖分成两个等腰三角形,原三角形的一个内角为36°,求原三角形最大内角的所有可能值.
解析:分下列三种情况进行讨论:
1.若原三角形为直角三角形,则它的最大内角为90°,如图6表示;
2.若原三角形三个内角的大小为α,2α,180°-3α且0°<α<45°:
(1)当α=36°时,2α=72°,180°-3α=72°,即原三角形的最大内角为72°,如图7所示;
(2)当2α=36°时,α=18°,180°-3α=126°,即原三角形的最大内角为126°,如图8所示;
(3)当180°-3α=36°时,α=48°,这与0°<α<45°矛盾,舍去.

图6 图7 图8
3.若原三角形三个内角的大小为α,3α,180°-4α且0°<α<45°:
(1)当α=36°时,3α=108°,180°-4α=36°,即原三角形的最大内角为108°,如图9所示;
(2)当3α=36°时,α=12°,180°-4α=132°,即原三角形的最大内角为132°,如图10所示;
(3)当180°-4α=36°时,α=36°,3α=108°,即原三角形的最大内角为108°,如图9所示;
综上所述,原三角形的最大内角为72°,90°,126°,108°,132°.

图9 图10
问题2 有一个等腰三角形纸片,若能从一个底角的顶点出发,将其剪成两个等腰三角形纸片,则原等腰三角形纸片的顶角大小为多少?
解析:分下列三种情况进行讨论:
(1)若原等腰三角形含有一个内角为90°,则显然无法从一个底角的顶点出发,将其剪成两个等腰三角形的纸片;
(2)若原等腰三角形三个内角的大小为α,2α,180°-3α且0°<α<45°:
①当α=180°-3α时,解得α=45°,这与0°<α<45°矛盾,不符合题意,舍去;
②当2α=180°-3α时,解得α=36°,此时原三角形的顶角为α=36°,如图11;

图11 图12 图13
(3)若原等腰三角形三个内角的大小为α,3α,180°-4α且0°<α<45°:
①当α=180°-4α时,解得α=36°,此时原三角形的顶角为3α=108°,
因为此时若能分成两个等腰三角形,则需要从顶角的顶点出发,如图12,不符合题意,舍去;
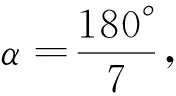
问题3n个等腰三角形的顶角α1,α2,α3,…,
αn两两不等.它们的共同特点是:被一条直线分得的两个较小三角形也是等腰三角形,求α1+α2+α3+…+αn的值.
解析:分下列三种情况进行讨论:
(1)若原等腰三角形含有一个角为90°,则显然可以利用斜边中线把它分成两个较小的等腰三角形,此时原等腰三角形的顶角大小为α1=90°;
(2)若原等腰三角形三个内角的大小为α,2α,180°-3α且0°<α<45°:
因为原三角形为等腰三角形,所以α=180°-3α或者2α=180°-3α,解得α=45°(舍去)或者α=36°,此时原等腰三角形的顶角大小为α2=36°,如图11;
(3)若原等腰三角形三个内角的大小为α,3α,180°-4α且0°<α<45°:
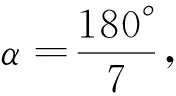
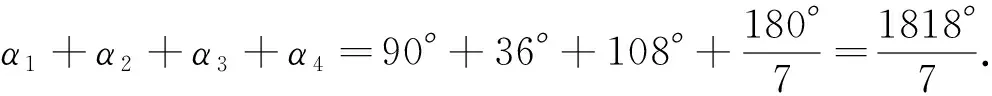
在解决一个三角形可以被切分成两个等腰三角形的问题中,如果仅凭直觉进行漫无边际的尝试,或者没能把握分类讨论的标准和方法,往往会浪费大量的时间和精力.如果能够结合这个三角形三个内角所要满足的条件,并且像问题1-3的解题过程那样进行分裂讨论,虽然有些过程稍显复杂,但却能帮助我们在分类讨论的时候做到有法可依,不重不漏,节约大量的时间和精力.
