基于二维Arimoto灰度交叉熵的图像阈值分割

杨昀臻 赵广州

（北京控制与电子技术研究所 北京 100038）

1 引言

图像分割是按照一定标准，将图像划分为互不重叠的区域，各区域内部具有相似的特征。图像分割是图像处理、图像分析理解的重要前期工作，分割结果的好坏直接影响到后期图像分析和理解的质量。阈值分割法是快速、简单、有效的分割方法，有着广泛的应用。但实际图像情况复杂，始终没有一种通用的分割方法，所以阈值分割方法一直是研究热点。Kapur［1］首先将信息熵的方法引入阈值分割，提出了最大Shannon熵阈值法。由于一维直方图没有考虑到图像的空间信息，当图像有噪声时，分割效果并不佳。因此，学者将最大熵法扩展到了二维，如Brink［2］基于灰度-领域平均灰度二维直方图，提出了二维最大Shannon熵分割法。二维阈值分割法的计算量增加到了O(L4)，算法运算速度过慢，有研究者将智能优化算法引入图像分割。如徐洪［3］等采用改进人工蜂群算法分割红外图像，吴一全［4］等引入粒子群算法来加速多阈值图像分割。

最大Shannon熵具有可加性，不适合描述具有非广延特性的物理系统，而图像具有明显的非广延特性，因此引入了 Renyi熵［6］、Tsallis熵［7～8］等广义熵来分割图像，取得了不错的效果。Arimoto熵［9］是Arimoto在研究有限参数估计问题时定义的一种广义函数，在决策误差估计中，可以得到误差概率上界，一些文献将Arimoto熵法运用于图像分割，取得了较好的效果［10～11］。

基于以上分析，本文利用Arimoto灰度熵，考虑了类内灰度分布［12～13］，结合交叉熵度量分割前后图像的差异的特点［14］，构造了Arimoto灰度交叉熵，并结合灰度-领域平均灰度二维直方图扩展到二维［15］。为加快运算速度，给出算法迭代计算中的一些递推公式，并引入改进人工蜂群算法，在基本人工蜂群算法的基础上引入混沌算子和自适应搜索半径等策略，提高算法收敛速度，平衡算法局部和全局搜索能力。

2 二维Arimoto灰度交叉熵阈值分割法

2.1 Arimoto灰度交叉熵定义

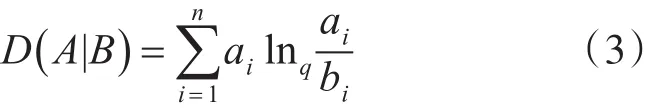
lnq(x)表示运算符，非广延交叉熵可以用作度量两相量间的距离，本文可将这概念引入Arimoto灰度熵中，在考虑类内灰度分布时，进一步考虑了分割前后图像的差异。

设f(m 。n)表示一幅尺寸为M×N，灰度级为L的图像，h(i)表示灰度级i的像素点出现的次数。假设阈值为t，则可将像素点分为两类，目标

令

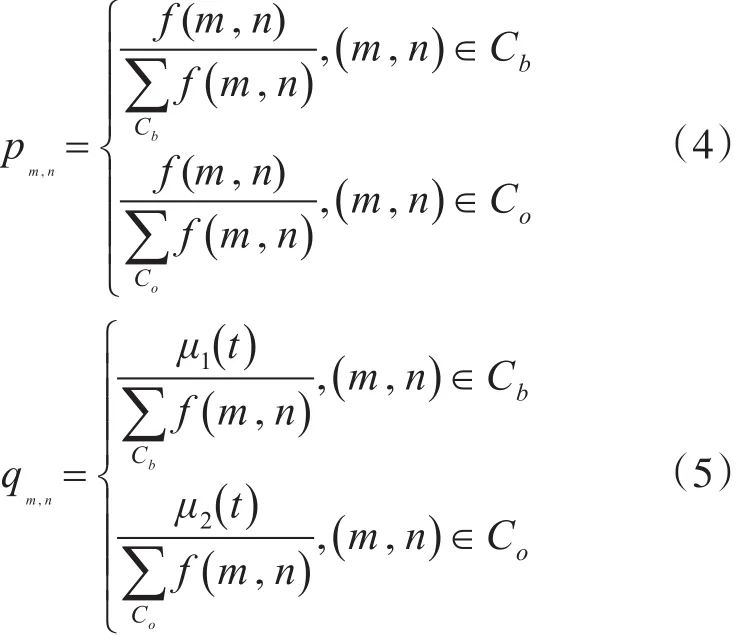
则根据以上分析可定义Arimoto灰度交叉熵的对称形式为

背景类交叉熵：

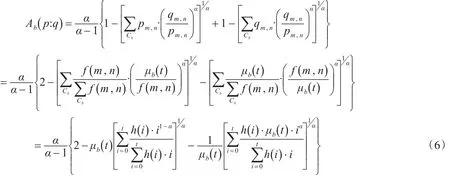
目标类交叉熵：

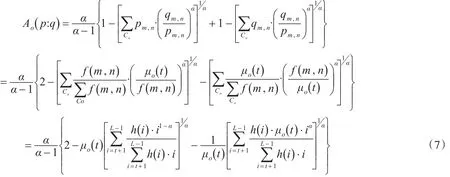
分割后总的交叉熵为

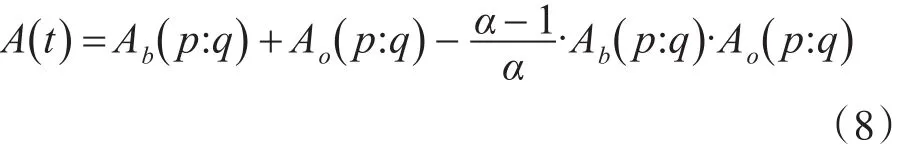
那么，当A(t)取最小时，得到分割最佳阈值：

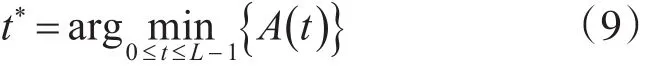
2.2 二维Arimoto灰度交叉熵阈值分割法

对于一幅大小为M×N，像素灰度为f(m 。n)，领域平均灰度值为g(m 。n )，令 h(i 。 j) 表示灰度对(i 。 j)出现的频数(i 。 j)表示像素灰度值和领域均值）。阈值(t 。 s)将二维直方图划分为4个区域，如图1所示，可设区域0代表背景区域，区域1代表目标区域。

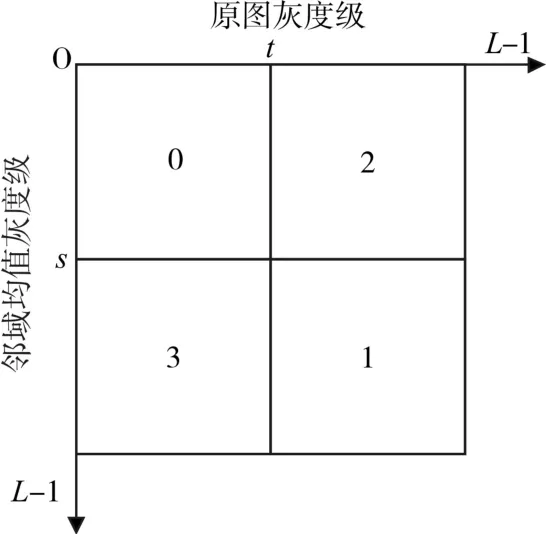
图1 灰度-领域均值二维灰度直方图

令

类似一维Arimoto灰度交叉熵，我们可以定义二维Arimoto灰度交叉熵。

对于背景类有：

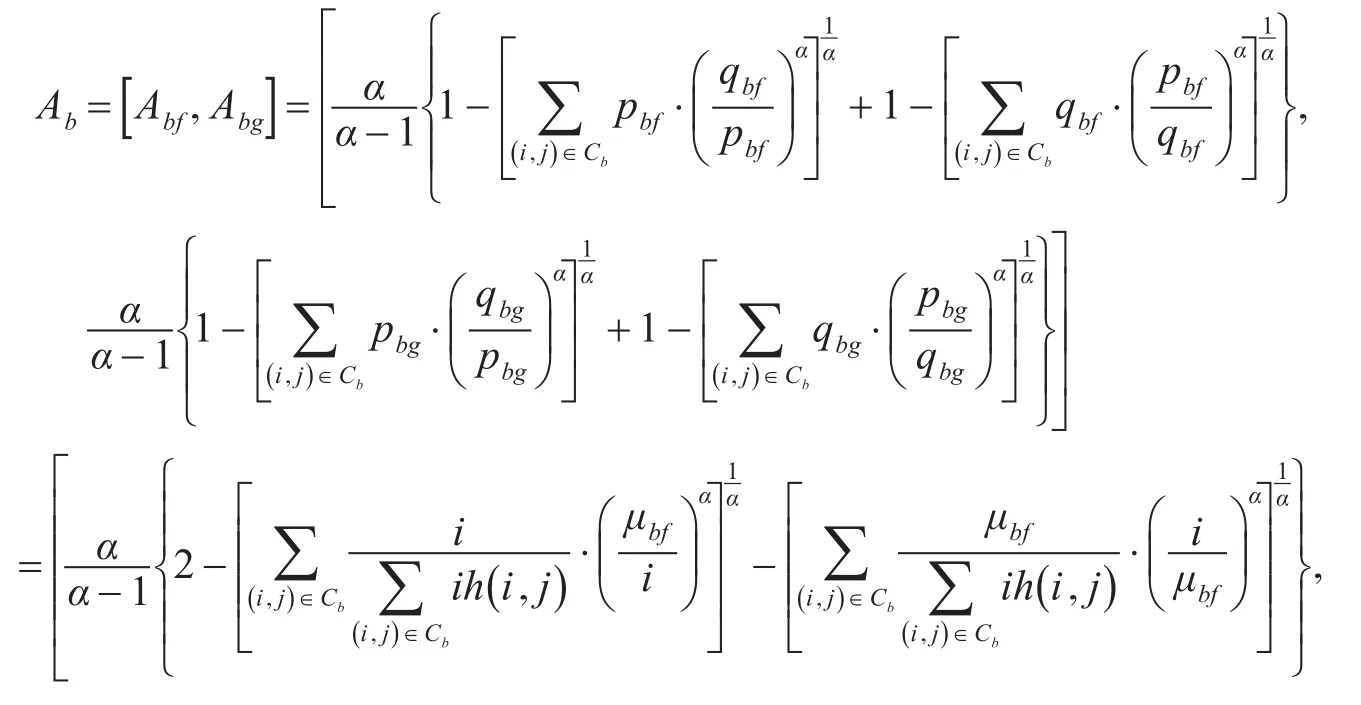
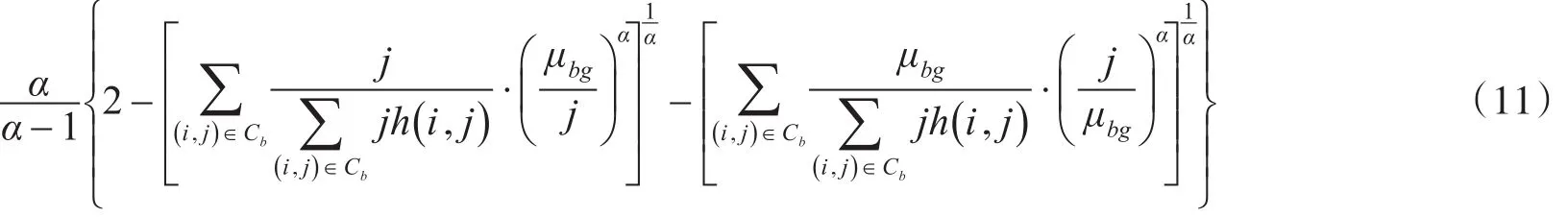
目标类Arimoto灰度交叉熵为

总的Arimoto交叉熵为

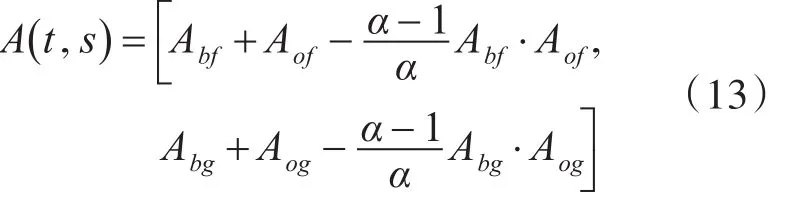
则二维Arimoto交叉熵阈值法的准则函数可选

为

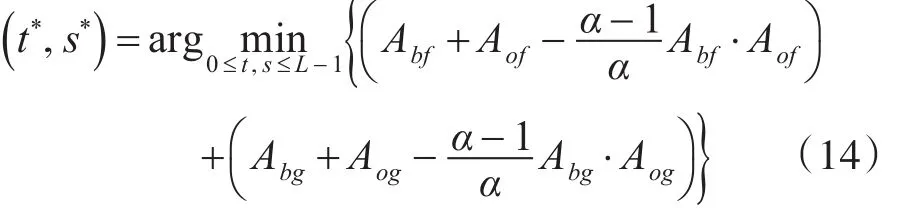
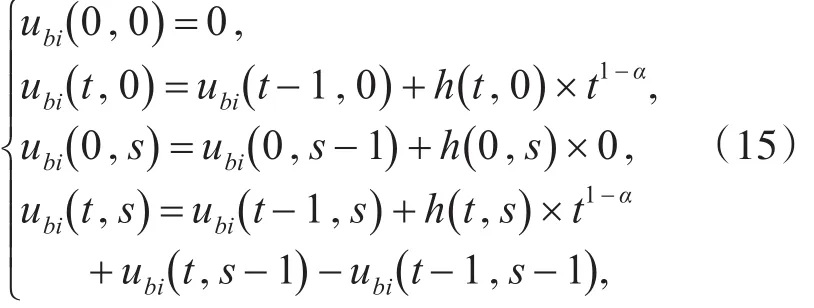
同理可推出其他中间变量的递推公式。

3 二维Arimoto灰度交叉熵的蜂群优化算法

人工蜂群算法主要模拟蜂群的采蜜行为，算法中包括引领蜂、跟随蜂和侦察蜂，具体问题中，蜜源的位置就是解空间的解，蜜源位置的维数就是解的个数。具体流程如下：

首先对食物源初始化，按式（16）产生ns2个

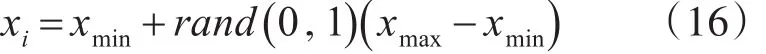
其次，引领蜂在食物源周围进行随机搜索，搜索公式如式（17）：

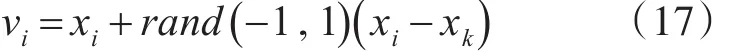
其中 k≠i。k∈{ }1。2…。ns/2 。

然后计算适应度值，选择适应度较优的称为下一代引领蜂。跟随蜂则根据适应度值的大小选择食物源，并在食物源附近搜索。当某一食物源连续nl次没有变化时，此处跟随蜂变为引领蜂，按照式（16）产生新的食物源。

重复以上步骤，直到达到迭代次数，停止循环。

上述的基本人工蜂群算法收敛速度较慢，而且容易陷入局部最优值，本文拟引入混沌算子、自适应调节搜索半径、结合历史最优信息的局部搜索，可有效提高搜索精度和速度。

1）使用logistic混沌算子初始化初始种群，迭代公式如下：

其中，ck∈(0 。1)。k=0。1。2… 式中变量在 μ=4 时该序列具有混沌运动的随机性和遍历性，可根据该变量初始化ns个食物源，选择适应度高的一半最为引领蜂：

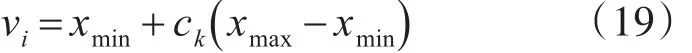
2）引领蜂的搜索可以引入最优引导搜索策略，设xbest()

k为第k次迭代跟随蜂中全局最优个体，则新的个体按下式产生：

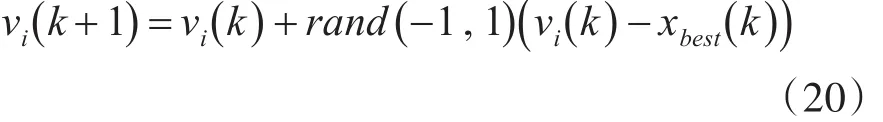
但上式在迭代后期很容易陷入局部最优，因此可以在引领蜂陷入局部搜索时（即引领蜂nl未改进），让引领蜂按式（17）产生新的个体，并与式（20）的进行比较，选择适应度较优的作为下一代引领蜂。

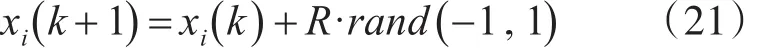
其中R为搜素半径，定义为

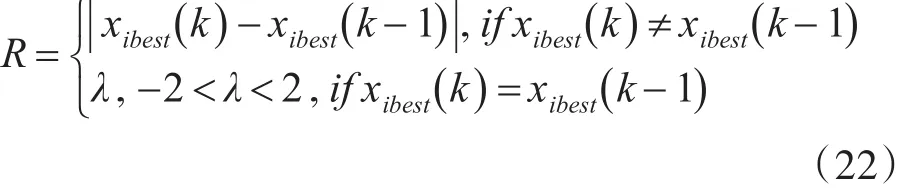
3）跟随蜂按下式进行搜索

这样在全局搜索阶段，搜索半径较大，当进入局部搜索时，半径变得很小，搜索半径可以自适应的调节。记录个体历史最优xibest()k和全局最优。

4）如果某一跟随蜂经过nl次迭代后，仍无改进，则按步骤2）更新食物源，作为新的引领蜂。判断是否达到最大迭代次数nmax，或者引领蜂更新次数达到nm次，若无返回步骤2），如果达到，则输出最优值，算法结束。

4 实验结果与分析

根据所提出的基于二维Arimoto灰度交叉熵的方法，针对大量的灰度图像进行分割实验，并与二维 Arimoto熵法［12］、二维 Tsallis交叉熵法［10］进行对比。所有实验在 Intel（R）Core（TM）i5-3470 CPU（3.2GHz），3.42G内存，Matlab 2013环境中运行。以lena，baboon，pepper，plane为例，其中plane图像添加了均值为0，方差为0.02的高斯噪声，邻域均值选8邻域。初始化种群ns为20个；最大迭代次数nmax为30次，跟随蜂连续不更新上限nl为3次，引领蜂累计更新上限nm为9次；Arimoto熵的参数α=0.01。

图2 Lena分割结果

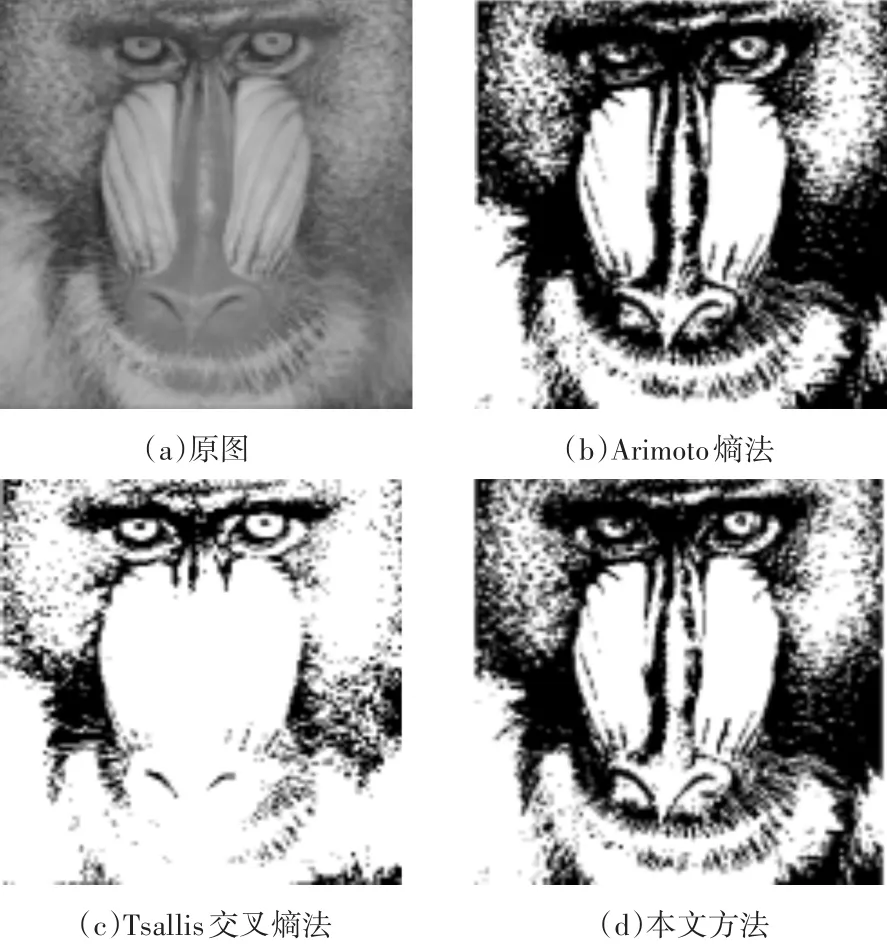
图3 Baboon分割结果

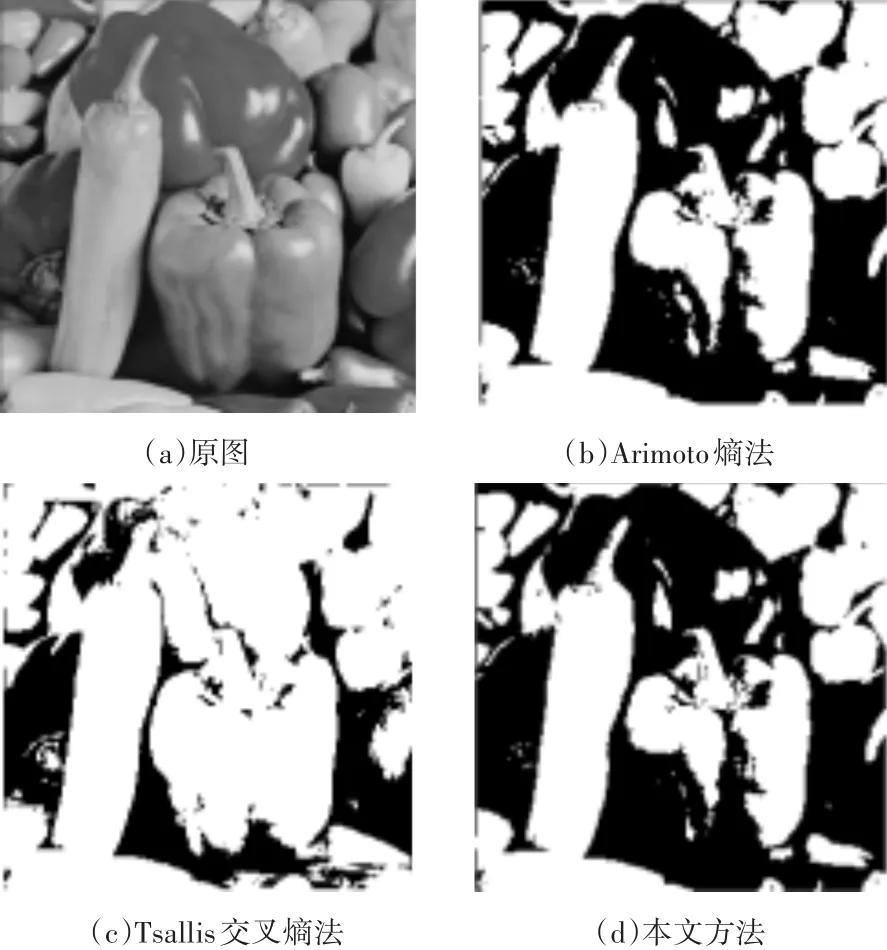
图4 Pepper分割结果

如图2所示，针对lena图像，三种方法均分割出了人像，但Arimoto熵和Tsallis交叉熵法均丢失了一定细节，尤其是嘴部、镜子中的细节，本文的方法准确、清晰地分割出了人像。图3结果中，baboon分割结果可以看出Arimoto熵法与本文方法结果相近，但Tsallis交叉熵法的分割结果不理想，狒狒的毛发、鼻子部分的纹理细节大量丢失。对于图4中pepper图像，Arimoto熵法与本文方法分割结果相近，Tsallis交叉熵法产生过度分割，目标细节丢失。图5中，对含噪声的飞机图像，Arimoto法和Tsallis交叉熵法都存在着较多的噪声干扰，分割结果不理想，而本文方法分割结果飞机轮廓清晰，噪声抑制效果较为满意。本文提出的方法针对纹理细节丰富的图像性能更优。

表1为各个算法计算结果与运行时间。从表可知本文方法的计算速度也快于或相近与Arimoto熵法与Tsallis交叉熵法。

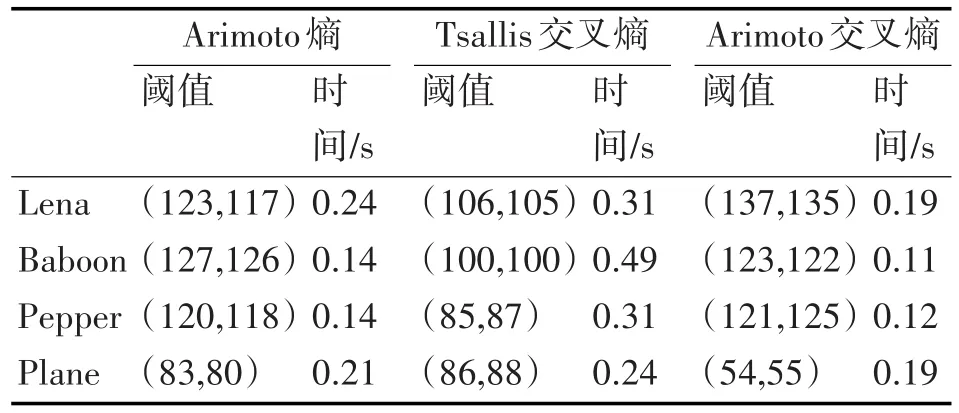
表1 分割方法结果与运行时间

5 结语

本文提出了基于灰度-领域均值灰度的二维Arimoto灰度交叉熵法。在Arimoto灰度熵基础上，结合灰度-领域均值灰度二维直方图划分方式，推导出二维Arimoto灰度交叉熵的阈值选择函数，给出中间变量的递推公式，并采用改进的人工蜂群算法，加速最佳阈值的搜索速度。与Arimoto熵法，Tsallis交叉熵法相比，本文分割后的图像目标区域更为完整，纹理细节丰富，同时抗噪性能良好，运行时间短。