基于伪逆的局部保留迭代哈希
2018-08-29杜仲舒王永利
杜仲舒 王永利 赵 亮
(南京理工大学计算机科学与工程学院 南京 210094)
1 引言
随着互联网时代的高速发展,产生的数据和其维度不断增加,快速准确地检索大量的高维数据越来越成为一个严峻的挑战。在解决这些问题的过程中,哈希学习受到了越来越多的人的关注。哈希学习将原始数据映射到一个二进制向量中,可以加快信息的查询检索速度,已经广泛应用于图像识别,数据挖掘,模式识别等领域。
局部敏感哈希算法(Locality Sensitive Hashing,LSH)是一种常见的近似最近邻哈希算法[1],尤其是在高维且数据量很大的情况下,很多传统哈希算法都会陷入“维数灾难”,而局部敏感哈希算法却能很好地克服这个问题,因此在音频识别,视频识别,网页去重,DNA序列相似比较等方向应用广泛。原始的lsh算法只是在汉明距离下进行处理。国内Li等提出了P-稳定分布(p-stable)的局部敏感哈希,将原始的汉明距离扩充到了欧式空间。
Yair等提出了谱哈希(Spectral hashing),把对数据特征向量的编码过程作为对图的分割问题来解决[4]。图的分割问题是一个NP难题,但是可以求出其松弛解,即的利用相似图的拉普拉斯矩阵求得阵特征值和特征向量,将原始特征降维。
Jae-Pil等提出了球哈希(Spherical Hashing)[6],使用超球平面代替超平面划分原始数据,原始特征空间Rd被球心为c和半径为R的超球面划分为球内和球外两个部分。由于超球面具有更强的区分性,超平面可以看做超球面半径无限大的特殊情况,球哈希提升了对高维数据检索的正确率。
本文提出了基于伪逆的局部保留迭代哈希(Pseudo-inverse locality preserving iterative hashing,PLIH)算法,构建邻接图并最小化近邻在低维空间的距离使得投影后的矩阵可以保持高维的近邻关系,解决了局部敏感哈希等无法有效保留高维近邻关系的问题。同时,采用伪逆替代逆矩阵解决了矩阵奇异的情况下求解投影矩阵失效的问题。最后通过迭代量化尽可能降低了投影矩阵在量化过程中的损失,通过与其他哈希算法在公开数据集上的比较,发现正确率和召回率都有5%~10%的提升,证明了该算法的可行性。
2 基于伪逆的局部保留迭代哈希算法
2.1 算法介绍
本文中哈希算法分为两个步骤,首先将高维数据进行投影,然后对投影后的数据进行量化。基于伪逆的局部保留迭代哈希(pseudo-inverse locality preserving iterative hashing),核心思想是利用数据点之间的近邻关系将高维数据中的非线性数据映射到低维空间,使其近邻关系保持较小误差。
2.1.1 基于伪逆的局部保投影
根据原始数据的近邻关系构建邻接矩阵,当出现以下情况可判定向量xi与xj邻接:
1)球形相近。当两个向量之间的距离小于ε。
2)K近邻相近。即一个向量在另一个向量的前K近邻中。
3)指定相近。在有监督情况下,两个向量已知是属于同一个类别。
构造权值矩阵W,使用热核计算方式:

为了保持近邻关系,最小化投影后的误差,有如下目标函数:
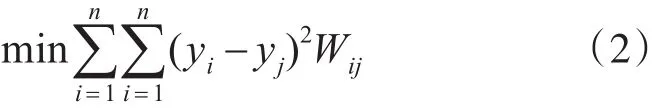
其中 yi和 yj是投影后得到的向量,Wij为邻接矩阵的权值。
为了求解上述目标函数,假定a是投影向量,y表示原始向量X经过a投影后的向量,我们有:
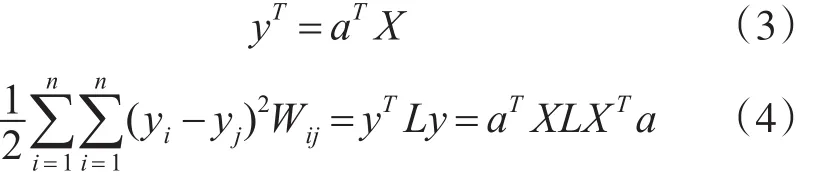
不失一般性,构建约束yTDy=1,目标函数
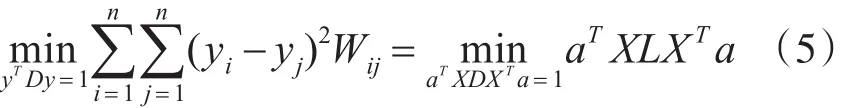
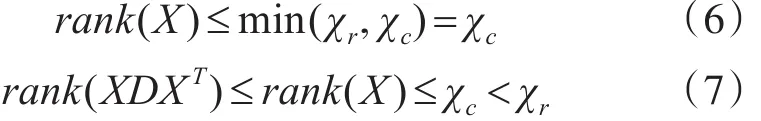
即 XDXT不满秩,故 XDXT不存在逆矩阵,出现奇异的情况。因此这里使用伪逆来解决不存在逆的情况,即投影矩阵为(XDXT)+XWXT。伪逆求解过程如式(8~10)。进行svd分解后获取奇异值中非零元素求倒数,重新组织后得到伪逆。
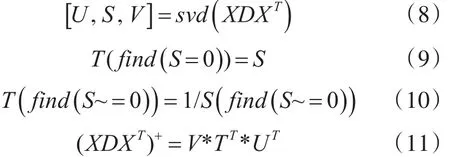
因此,基于伪逆的局部保投影可以保证投影过程的鲁棒性,解决采样率不足情况下不存在逆矩阵的情况,同时有效保持原始数据中的近邻关系。
2.1.2 迭代量化
对于给定一个投影得到的固定维度的向量Y,需要将其量化到一个二进制向量B。由于传统方法更多地关注于投影方法的优化,而忽略了量化的过程。传统的方法使用零作为量化的阈值,很容易就能将其二进制量化为sgn(Y),但是这样量化会影响哈希的准确度,因为量化过程中,很多信息通过量化损失掉了,所以很有必要提出一种更有效的量化方案。
PLIH中的迭代量化过程可看做使用超立方体来近似样本点的过程,对Y施加一个正交变换可以保持原有的距离关系。为了减少量化损失,我们将量化的目标函数表示为
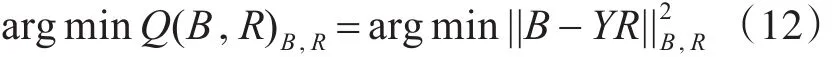
这里的B∈{-1。1}n*c,c是二进制串的长度,R为旋转矩阵。二维空间中直接以均值0为阈值的量化方法,随机旋转的投影和PLIH中使用的迭代量化的量化结果如下:
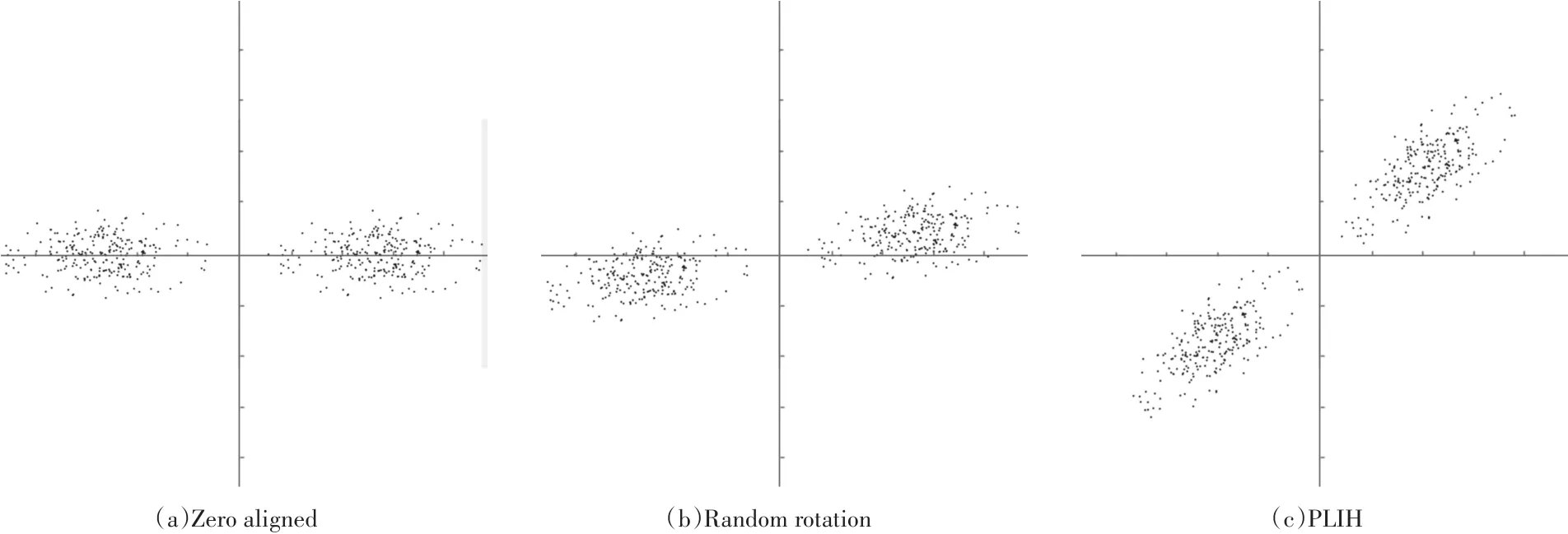
图1 阈值为零量化,随机旋转的投影量化PLIH中使用的迭代量化
1)固定R更新B。
由于正交投影矩阵R是固定的,因此最小化方程等价于:
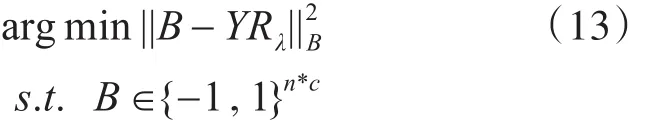
不难验证,问题的最优解可以取正交变换后的正负符号函数即可,即B=sgn(YRλ)。
2)固定B更新R。
对于固定的B,目标函数对应于传统的普罗克汝斯忒斯正交问题,即寻找一个最佳的旋转方向来对齐所有的点。问题转化为
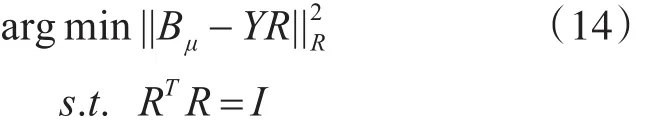
由矩阵分析理论得到,原问题等价于最大化矩阵秩的问题,即max tr(BμRY),s.t.RTR=I。由于Bμ是固定量,使用奇异值分解,令BTY=UΩVT,可得R=VUT是一个最优解。迭代交替更新B和R,便可以找到全局最优的量化方案满足目标函数,最小化量化过程中的信息损失。
2.2 PLIH算法流程


3 实验及结果分析
实验平台为Matlab2016a,算法在cpu为3.2GHz、内存为16G的计算机上运行。实验采用了经典的gist_CIFAR和cnn_Caltech数据集,对比了经典的哈希算法和目前效果相对较好的近似最近邻 算 法 ,例 如 ITQ,LSH,PCAH,SH,PCA-RR,DSH,SpH[10~15]等算法。
ITQ是基于PCA降维的迭代量化算法,LSH使用的是从高维正态分布中产生随机矩阵的方法,SPH降维采用的是将高维向量投影到超球面的算法。从实验结果可以看到,PLIH相对其他算法正确率与召回率都有较大的提升,尤其在比特位数较少时优势更为明显,证明了PLIH可以有效地保留近邻间的相似关系。
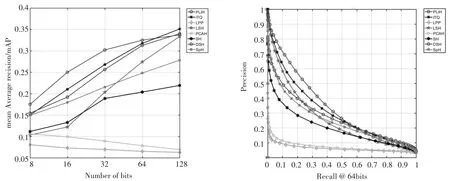
图2 gist_CIFAR数据集上多种哈希算法的正确率与召回率
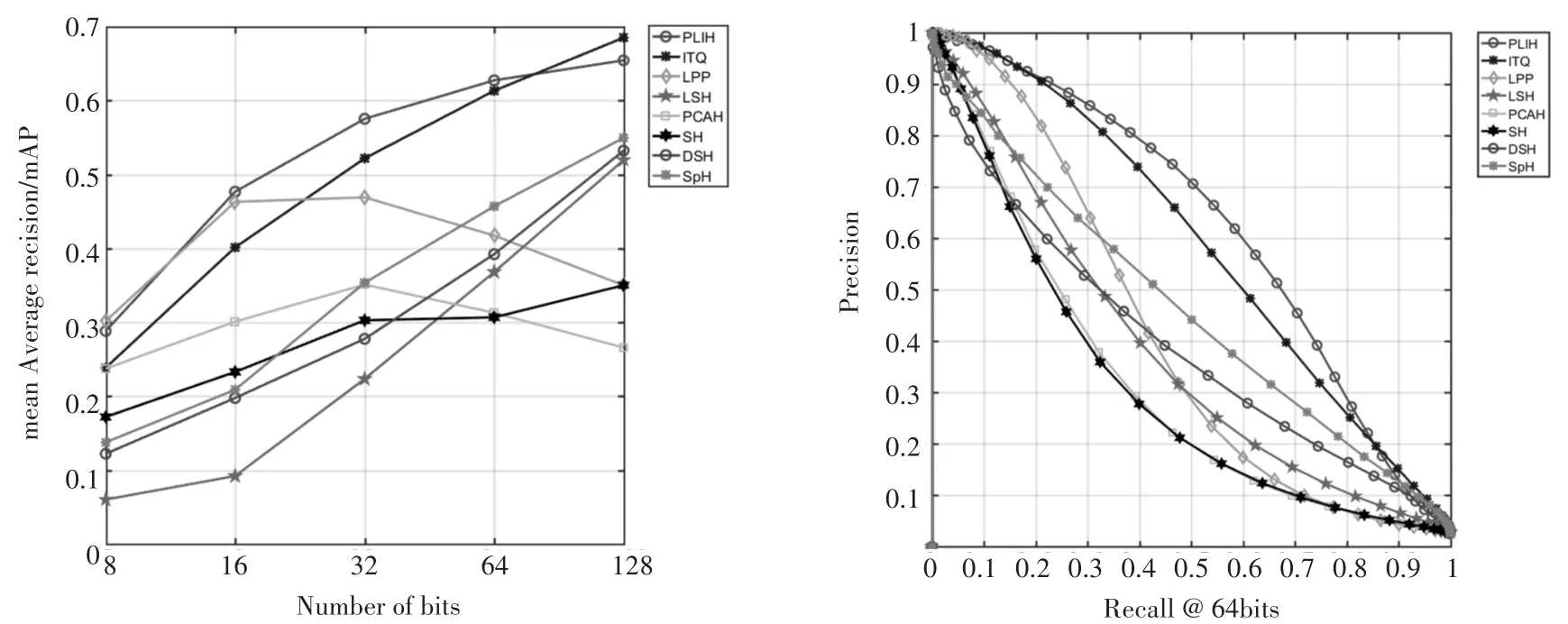
图3 cnn_Caltech数据集上多种哈希算法的正确率与召回率
4 结语
在本文中,提出了一种新的近似最近邻检索算法,可以有效保持数据的近邻关系,同时解决了哈希过程中的矩阵奇异和量化损失较大的问题。实验证明,基于伪逆的局部保留迭代量化算法的具有良好的效果。本文中的哈希方法是线性正交的,部分高维数据中的数据并不一定可以在线性空间中得到有效表示,因此接下来的工作可以关注非线性的数据特征处理,以便获得更高的正确率和召回率。
