基于Moreau-包络的近似平滑迭代磁共振图像重建算法

刘晓晖，路利军，冯前进，陈武凡

(南方医科大学 生物医学工程学院，广州 510515)(*通信作者电子邮箱chenwf@fimmu.com)

0 引言

磁共振成像(Magnetic Resonance Imaging, MRI)因其成像中不使用电离辐射、可以更灵活地选择成像参数、对软组织结构及代谢功能的完美表达以及对许多特定参数更加敏感等优点成为临床应用中性能最卓越的医学成像方式之一[1-2]。然而，MRI特殊的成像机制导致的相对较慢的成像速度阻碍了MRI进一步的发展和应用：磁共振(MR)图像对于运动非常敏感，因而成像时间长会产生更多的运动伪影，这种情况常常导致需要对病人进行镇静或麻醉；较低的空间分辨率限制了MR对某些和呼吸相关的部位的成像，如腹部成像和心脏成像；较长的扫描时间在增加成像成本的同时也会限制MRI的适用病人范围[3]。出于这些原因，许多研究人员在寻求在减少采样数据的同时又不降低图像质量的成像方法。

从20世纪70年代MR还未被广泛地应用于临床以来，MRI的加速问题就被广泛的探讨和研究。MRI中成像数据为Fourier变换空间，通常称为k空间。MRI的采样时间主要由k空间的分段采样模式所决定，在给定一个采样序列以后，k空间中的分段数就决定了MR图像的信号采集时间。基于这个原因，MRI的加速通常是采用减少k空间中的分段数，即对k空间进行降采样。这种方法利用了k空间的冗余特性，即k空间中的各个点是由位于成像物体不同空间位置的信号叠加产生的[4]，主要代表技术是并行MRI(parallel MRI, pMRI)技术[5-8]。pMRI技术利用多组线圈同时接收MR信号，利用线圈的空间敏感度差异来代替部分梯度编码，从而减少梯度编码步数，节省扫描时间。pMRI无需修改成像序列，在保持扫描视野和空间分辨率不变的情况下减少成像时间，因此为现代商业MRI系统广泛采用，成为目前的常规扫描方法。然而，由于欠采样导致的混叠伪影，以及重建算法对噪声的放大效果，pMRI方法在实际临床应用中只能使用小加速倍数以保证理想的重建质量。

近年来在信号处理领域发展起来的压缩感知(Compressed Sensing, CS)[9-12]理论为快速MRI技术提供了一种新的可能。CS理论认为，一个本身稀疏的或者可压缩的未知信号，选择一组合适的感知信号(即感知矩阵)，在感知信号个数远小于原始未知信号维数的情况下，通过求解一个非线性最优化问题，可以精确恢复出原始信号。在MRI中：1) MR图像被认为是稀疏(如血管MR图像、三维MR图像相邻图像层之间以及动态MR图像在时域上的图像序列)或是可压缩的(一幅MR图像在某个变换域中的系数矩阵具有可压缩性)；2) MRI的感知信号空间是Fourier空间，其成像方式决定了可以有选择的扫描k空间中的一部分数据。上述两个条件决定了CS可以应用于快速MRI中，这种快速MRI技术一般称为CS-MRI。

CS-MRI通常需要求解一个包含稀疏正则项的非线性凸优化问题。为了更好地表达MR图像的稀疏性，CS-MRI的数学模型中往往包含两个稀疏正则项，即优化问题中包含三个函数：数据保真项、1范数稀疏正则项和MR图像的总变分(Total Variation, TV)正则项；而经典的近似迭代类算法求解的是包含两个函数(通常为数据保真项和一个正则项)的最优化问题，所以在使用近似点迭代类算法的CS-MRI方法中，通常的做法是将初始优化问题根据正则项分解为两个优化子问题，分别对这两个子问题用近似迭代算法进行求解得到相应的解，再对求得的两个解取平均值得到最终解。这类算法由于每个子问题的输入变量相同可以称为多正则项优化问题的并行求解方法。

近似迭代算法主要是针对优化问题中存在的非平滑函数，如1范数正则项、核范数以及TV项等，这些非平滑函数不能直接求导，因此在优化算法中需要求取它们的次梯度，在近似迭代类算法中往往使用近似算子来求解这个次梯度，近似算子本身即为一个最优化问题的求解过程，通过对输入信号x0迭代地施加近似算子即可求解原始优化问题的最优解。在前面提到的多正则项优化问题的并行求解算法中，两个子问题的解在同一个迭代步骤中是互相独立的，即互相不以对方为输入，这类算法在两个子问题的求解过程中没有任何优化步骤。针对这个问题，本文提出一种基于Moreau包络的近似平滑迭代算法(Proximal Smoothing Iterative Algorithm, PSIA)，该算法首先将原始优化问题中的一个非平滑正则项的梯度用它的平滑函数的梯度近似表示，然后把数据保真项和平滑后的正则项的线性组合看作一个平滑可导函数，最后利用经典的近似迭代算法对优化问题进行求解。

1 磁共振图像稀疏重建相关算法

在文献[4]中，对CS-MRI的理论基础及数学模型都作了详细的探讨，并证明了在附加一个1范数小波变换约束项和TV约束项的前提下，可以从降采样的k空间数据中准确地重建出MR图像，并提出如式(1)中的非约束凸优化问题：

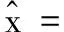
α‖Wx‖1+β‖x‖TV

(1)

其中：x∈RN×N为待重建的MR图像，N×N为MR图像尺寸；Fu:RN×N→CM×N(M≤N)，为降采样Fourier变换，是传感矩阵作用于Fourier矩阵的结果，即Fu=SF，其中S∈RM×N，F:RN×N→CN×N分别为传感矩阵和Fourier变换；b∈RM×N为k空间降采样数据；W:RN×N→RN×N为小波变换；‖·‖TV:RN×N→R为MR图像的TV值；α，β>0为正则项权重系数。式(1)中的几个范数定义分别为式(2)～(4)：

(2)

(3)

(4)

式中D1、D2为分离梯度算子，分别表示对图像x作水平、垂直两个方向满足Neumann边界条件的前向有限差分：

(5)

并满足下面的Neumann边界条件：

(6)

式中n1、n2满足n1,n2∈[1,N]。对于问题式(1)的求解，最主要的困难来自于第二项小波变换1范数和第三项TV项，这两项都不能直接求取微分或导数，因而不能对问题式(1)直接使用梯度法求最小值。针对这个问题，文献[4]提出了共轭梯度(Conjugate Gradient, CG)下降算法来求解问题式(1)，但是这种算法的缺点是收敛速度慢，对于一幅512×512像素大小的图像，CG重建出视觉效果比较好的图像所需要的时间是2 min～3 min，即使重建一幅256×256像素大小的图像，也需要十几秒，当对三维物体成像时，所需时间就要以小时计，这显然不能满足实际应用的需要。

为了提高重建速度，考虑到问题式(1)的正则项是两个截然不同的范数表达式，数学优化算法中的分离算法被用来解决式(1)这样的多个正则项优化问题。分离算法主要包括算子分离算法和变量分离算法。算子分离算法的核心问题是寻找最小化问题所对应的最大单调算子为零的解，经典的算子分离算法有forward-backward算法[13]、Douglas-Rachford算法[14]和Peaceman-Rachford算法[15]，它们都是求解目标函数为两个函数和的最小化问题的算法。与之相对应的，变量分离算法则是使用变方向法(Alternating Direction Method, ADM)求解最小化问题的增广拉格朗日形式。变量分离算法是Douglas-Rachford算法和Peaceman-Rachford算法的优化变形，最早在20世纪70年代被提出用来解决偏微分方程(Partial Differential Equation, PDE)问题[16]。近来，在文献[17]中提出了变量分离算法可以用来解1范数和TV正则优化问题。文献[18]和文献[19]分别提出算子分离类方法TV1范数压缩MRI(TVl1Compressed MR Imaging, TVCMRI)算法与变量分离类方法部分k空间重建算法(Reconstruction from Partial k space algorithm, RecPF)来求解问题式(1)。这两种算法都比算法CG要快，重建一幅像素为256×256的磁共振图像所需时间为2 s～3 s，在保证重建准确度的前提下，大幅提高了重建速度。然而由于分离算法的特点，这两种算法人为添加了一定数量的辅助变量，使得算法代码的复杂性较大，从而算法的重现具有一定的难度；另外，这两种算法中，对于两个正则项求导过程中的近似处理都是简单地加上一个非负二次项，对于算法的简化没有贡献。

针对以上问题，近似迭代算法被引进非平滑正则约束的优化问题中。近似迭代算法的基本原理是给出非平滑函数的近似算子[20]，这个过程就是一个求取子问题的最小化的过程。对给定一个初始点的原问题式(1)，迭代地算出它的近似点，即可求解得出理论上的最优解。这类算法和前述几类算法不同的地方在于：直接对非平滑项的近似算子进行操作，而不是对非平滑项求取梯度或是微分[21]。两种最著名的近似迭代算法是迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm, ISTA)[22]和它的加速形式——快速迭代收缩阈值算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA)[23]，这两种算法被提出用来求解两个函数和的最小化问题。在快速复合分离算法(Fast Composite Splitting Algorithm, FCSA)[24-25]中将问题式(1)分解为两个子问题，即数据保真项与小波变换1范数的和的最小化问题以及数据保真项与TV项的和的最小化问题，分别对这两个问题使用快速迭代收缩阈值算法，将求得的解取平均，即认为所得的值为问题式(1)的解。在FCSA中，两个最小化子问题的权重被简单地取值为0.5，然而在实际应用中，这两个子问题的权重则根据实际所要重建的磁共振图像的内容而有所不同，这就向算法的鲁棒性提出了挑战。本文提出的重建算法则避免了这个困扰，即不对问题式(1)进行子问题分离，利用近似平滑方法的数学特性求解。

2 快速近似平滑迭代算法

2.1 相关快速重建算法

在给出本文算法之前，先讨论目标函数为两个凸函数线性组合的优化问题的求解。近似迭代类算法FISTA被用来求解式(15)所示两个函数和的最小化问题：

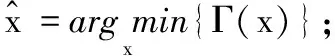
Γ(x)=p(x)+q(x):x∈RN×N

(7)

其中:p(x)为一个凸的Lp平滑函数;q(x)为一个不可微的连续凸函数。FISTA提出通过迭代地求解函数q(x)的近似点便可得到问题式(7)的最优解，即：

xk+1=proxq(xk-η▽p(xk));

(8)

其中：xk+1、xk分别为第k+1与第k次迭代求得的解；▽p(x)为函数p(x)的导数；proxq(x)为函数q(x)在x处的近似值函数。

FISTA算法伪代码为：

步骤1 参数及变量初始化：

参数：正则化参数α,β，迭代计数k=1，近似算子参数

η=1/Lp。

变量：图像变量x0=0，y1=0，加速步长变量θ1=1。

步骤2 变量迭代：

Fork=1,2,… do

xk=proxq(yk-η▽p(yk))

yk+1=xk+((θk-1)/θk+1)(xk-xk-1)

End for

算法FCSA将问题式(1)分解为两个子问题，分别是小波1范数正则约束问题和TV正则约束问题，利用FISTA对这两个问题求解后所得解为x1、x2，再取平均即为问题式(1)的解。本文将提出另外一种利用算法FISTA求解问题式(1)的近似平滑迭代算法(PSIA)。

2.2 近似平滑迭代算法

本文需要求解的问题式(1)是由三个函数线性组合而成，将问题式(1)简化表达为：

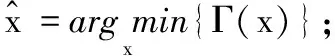
Γ(x)=f(x)+g(x)+h(x):x∈RN×N

(9)

其中f(x)、g(x)和h(x)的表达式分别为：

(10)

如果要对问题式(9)使用算法FISTA进行求解，则对照式(8)可得其变量近似迭代步骤为：

xk+1=proxh(xk-η▽(f+g)(xk));

(11)

式中的proxh(x)在已知x时很容易求得，而导数▽(f+g)(x)由于函数g(x)的非平滑性不能直接求取。为了得到▽(f+g)(x)的表达式，首先要对函数(f+g)(x)进行平滑近似，由于函数f(x)是平滑函数，因此平滑近似主要是对函数g(x)进行。在凸优化理论[26]中，可以通过求解非平滑函数的Moreau包络来对其进行平滑近似，其定义为：

定义1 Moreau包络[26]。对于一个非平滑不可微函数g(x):RN×N→R∪{+∞}，它的Moreau包络为：

(12)

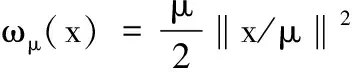
定理1[27]给定函数g(x)为一个下连续的非平滑凸函数且μ>0，则由定义1给出的Moreau包络为一个1/μ平滑函数，且其导数可由g(x)的近似算子得到：

▽(gμ)(x)=(x-proxg(x))/μ

(13)

其中proxg(x,μ)的表达式为：

(14)

此时式(11)中的导数▽(f+g)(x)中g(x)部分可由式(13)给出。

本文提出求解优化问题式(9)的近似迭代算法为：首先对非平滑函数g(x)使用Moreau包络进行平滑近似，则得到一个新的优化问题：

Γμ(x)=f(x)+gμ(x)+h(x):x∈RN×N

(15)

在优化问题式(15)中，由于函数f(x)、gμ(x)都是定义域为x∈RN×N的平滑凸函数，因此可以将这两个函数的和看成一个新的函数K(x)，则式(15)可以表达为：

K(x)=f(x)+gμ(x):x∈RN×N

(16)

对问题式(16)，使用算法FISTA进行求解，其变量迭代步骤为式(11)。

本文算法伪代码为：

步骤1 参数及变量初始化：

参数：正则化参数α,β，迭代计数k=1，近似算子参数μ=1/Lf,η=1/(Lf+1/μ)。

变量：所求取图像变量x0=0，中间变量y1=0，加速步长变量：θ1=1。

步骤2 变量迭代求解：

Fork=1，2，… do

xk+1←proxh(yk-η▽(f+gμ)(yk));

yk+1=xk+((θk-1)/θk+1)(xk-xk-1)

End for

迭代步骤1中▽(f+gμ)的计算如下：

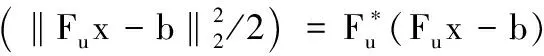
(17)

▽(gμ)(x)=(x-proxg(x))/μ=

(sign(Wx).×max{0,Wx-μ/Lf})/μ

(18)

(19)

由此可知上述算法PSIA中的所有计算单元都已知，给定一个初始点，即可迭代地计算出重建图像。

3 实验结果与分析

3.1 实验设置

为了验证算法的有效性，将本文提出的近似平滑迭代算法(PSIA)与第1章中提到的4种经典稀疏MR重建算法的重建结果进行对比，这4种重建算法分别为：CG、TVCMRI、RecPF和FCSA，选取这些算法进行对比是因为它们求解的目标函数和本文一致，且它们都是经典的磁共振稀疏重建算法。本文算法与对比算法都是在Inter Core i5- 2400、3.10 GHz CPU的PC上进行，编程环境使用Matlab 2015b，每个算法的迭代次数都是50。使用4种图像数据进行重建结果对比，分别是：经典的Shepp-Logan体模图像、人脑MR图像、手部MR图像，以及脑部血管MR图像；为了方便对比，所有图像尺寸都设为256×256像素大小，灰度取值范围为0～255；实验降采样率约为20%，采样矩阵与实验图像数据如图1所示；在实验中，对采样数据添加标准差为σ=0.01的高斯白噪声以模拟采样中产生的噪声。

图1 采样矩阵与四种参考实验图像

算法中的参数设置为：正则化参数α、β分别设为0.035和0.001，这个取值与4种对比算法中相同，以便于算法效果的比较；近似算子参数的设置根据Lipschitz常数分别设置为：1，0.5。

3.2 实验结果评估标准

本文主要给出两大类实验结果评估标准，分别为定性评估即视觉效果评估，以及定量评估包括信噪比(Signal-to-Noise Ratio, SNR)、相对误差(Relative Error, RE)和结构相似度指数(Structural SIMilarity, SSIM)[28]，另外还给出了算法复杂度对比(CPU时间)。其中SNR、RE和SSIM的表达式为：

(20)

3.3 实验结果及讨论

四种实验图像在五种不同算法(CG、TVCMRI、RecPF、FCSA和PSIA)中的重建结果与重建结果对应的差值图像如图2～5所示。在差值图像的表示中，为了比较的公平性，在每个图像的结果表示中，将重建结果最差的算法对应的差值图像灰度值作为灰度直方图范围。

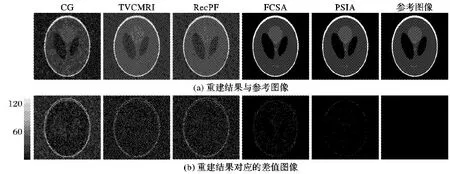
图2 Shepp-Logan体模的重建结果

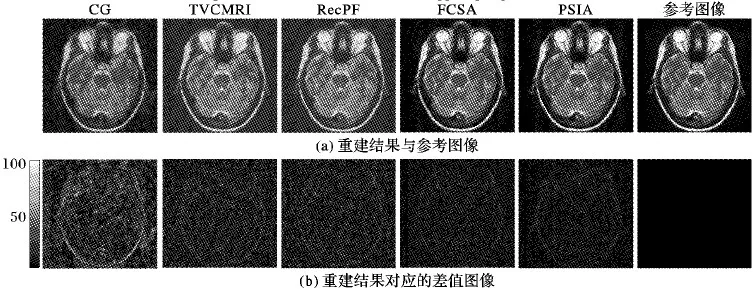
图3 脑部MR图像的重建结果

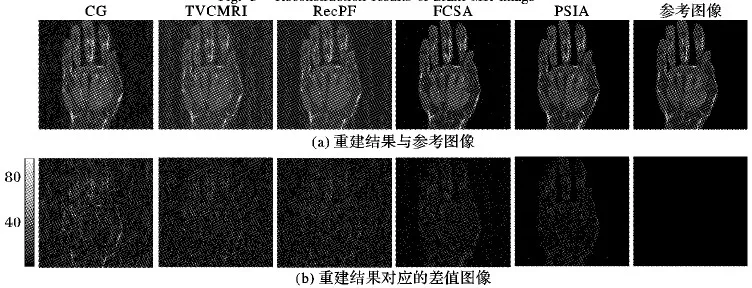
图4 手部MR图像的重建结果

从图2～5中可以看出：本文提出的重建算法PSIA在重建的视觉效果上比之前的几种经典算法都要好，具体体现在差值图像中的边缘细节的重建以及对噪声的消除上。算法CG的重建效果最差，不仅没有很好地消除引进的高斯白噪声，在图像的边缘和解剖学结构上都丢失了很多细节；算法TVCMRI和RecPF的重建结果在视觉效果上相近，且同时在细节的恢复和噪声的消除上优于CG；算法FCSA比TVCMRI和RecPF得到更好的重建结果，具体体现在消除了更多的噪声，使重建图像看起来更“干净”；本文提出的算法PSIA比起FCSA在去噪方面表现更好，具体表现在差值图中图像背景部分的噪声更小，在图像细节的恢复上也更好，在视觉上与参考图像以及真实MR图像更接近。

四幅图像在五种重建算法中的SNR与迭代次数的关系如图6所示，用来比较算法的收敛性。

从图6可以看出，对于不同的重建图像，算法CG的效果是最差的，体现为SNR值最低；TVCMRI和RecPF的重建效果相近，这可以从算子分离和变量分离这两类算法的关系推测出原因：变量分离类算法是算子分离类算法的优化变形；FCSA和本文中提出的PSIA算法的重建效果比前三种算法要好，而本文提出的算法PSIA在四个重建图像上的重建结果都好过FCSA，这验证了第1章中的讨论，即：简单地将两个子问题的权重设为0.5带来鲁棒性问题，导致了虽然都是使用快速迭代收缩阈值算法(FISTA)，PSIA比FCSA的重建效果要更好。

表1～4给出了四种图像不同算法50次迭代后的重建性能，包括SNR、RE以及SSIM；同时为了比较算法复杂度，给出了每个算法运行的CPU时间。SNR给出了重建图像与参考图像的信噪比，SNR的值越大，认为重建算法的重建效果越好；RE给出了重建图像和参考图像间的差值，RE的值越小，认为重建算法的重建效果越好；SSIM给出了重建图像和参考图像间的相似度测量，SSIM的值越大，认为重建效果越好。

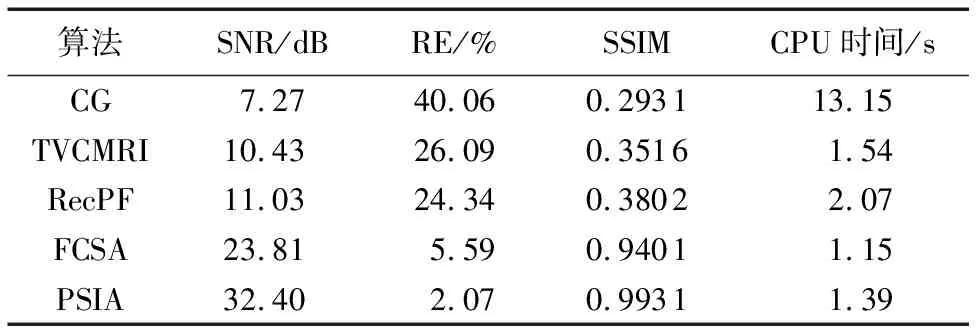
表1 Sheep-Logan体模的重建性能

从表1～4可以看出，在这三个评估参数方面，PSIA都是最好的，同时也可以看出算法CG的结果是最差的，算法TVCMRI和RecPF表现相近，FCSA优于前三种算法，比PSIA表现差，这与图2～5中的视觉评估以及图6中的SNR随迭代次数变化的结果一致。在CPU时间上，算法CG运行时间最长，从TVCMRI开始算法运行时间即加速到十倍数量级，RecPF的运行时间和TVCMRI相当，FCSA比以上两个算法都要快，这得益于快速迭代收缩阈值算法的使用，PSIA在时间上和FCSA相当，这也与两者使用的核心算法都是同一种算法所得出的推断一致。

图5 脑部血管MR图像的重建结果

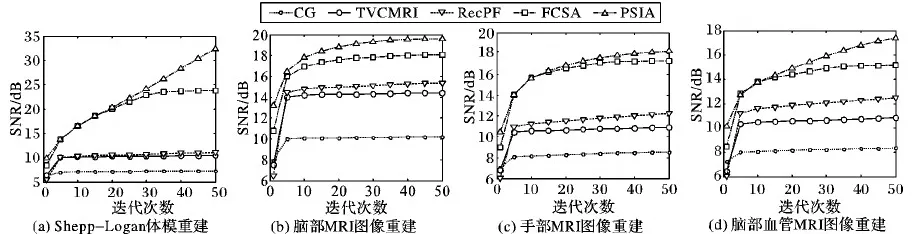
图6 四种MR图像重建结果的SNR

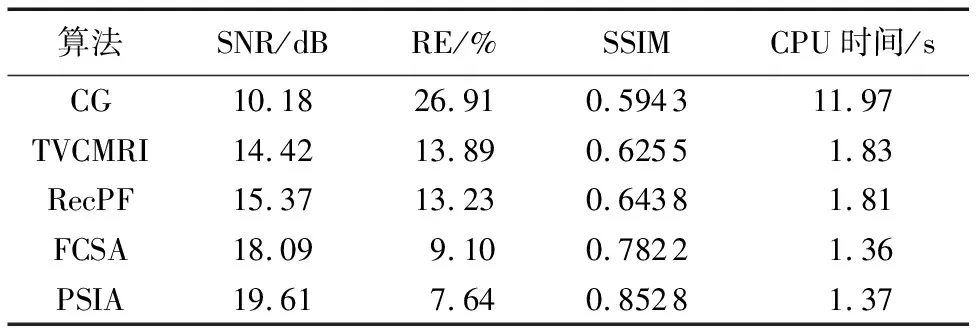
算法SNR/dBRE/%SSIMCPU时间/sCG10.1826.910.594311.97TVCMRI14.4213.890.62551.83RecPF15.3713.230.64381.81FCSA18.099.100.78221.36PSIA19.617.640.85281.37

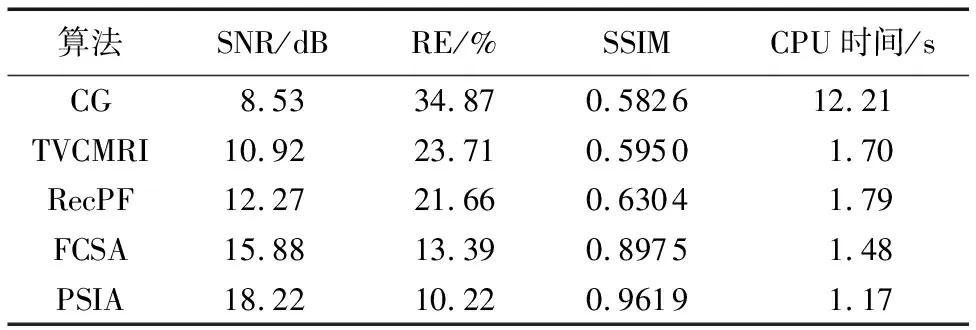
表3 手部MR图像的重建性能

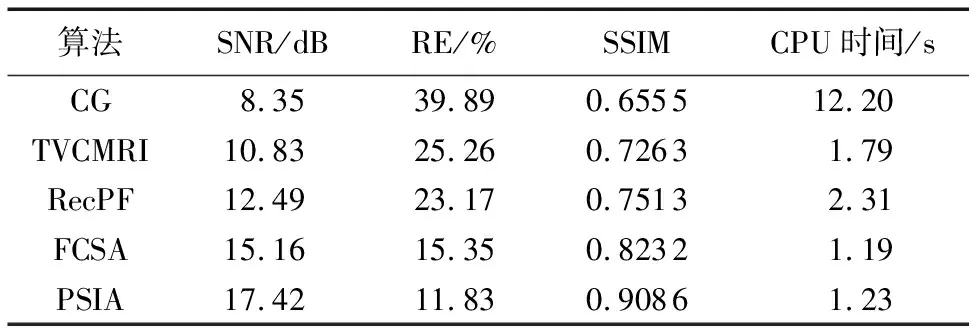
表4 脑部血管MR图像的重建性能

4 结语

针对现有的MR图像稀疏重建算法中不能在一个迭代计算步骤中同时对两个正则约束项同时施加近似算子的问题，提出了一种基于Moreau-包络的近似平滑迭代算法，该算法具有以下特点：

1)使用基于近似平滑迭代的算法，使算法结构简单、易于重现；

2)与同样基于近似平滑迭代的算法FCSA相比，解决了将原始最小化问题分解为两个子问题时面临的权重设置问题；

3)此算法可以应用在不同正则约束稀疏化重建问题，在算法PSIA中，只要给出相对应的正则项的近似算子，即可直接使用该算法。

对仿真体模以及真实MR图像的实验结果表明，本文提出的近似迭代算法在重建精度以及算法复杂性方面都有很好的表现，重建效果比当前经典的CG、TVCMRI、RecPF和FCSA都要好，在算法复杂度方面和最快的算法FCSA相当。

下一步的工作主要有两方面：一是对算法中参数的优化，在本文算法PSIA中，近似算子参数μ、η取的是固定的常数，在优化算法文献中，提出可以对这类参数进行优化从而得到更好的重建结果；二是提出新的正则约束项并利用算法PSIA，尤其是针对TV约束项，目前已有多种对于总变分的变形以及新的定义，将这些新的约束用在重建中预期将得到更好的重建结果。