数据库中不等式查询语句的resilience计算

林 杰，覃 飙，覃雄派

(中国人民大学 信息学院，北京 100872)(*通信作者电子邮箱qinbiao@ruc.edu.cn)

0 引言

近几十年来，科技得到飞速发展，数据呈爆炸式增长，信息革命推动了各个学科的共同发展，许多方向的发展由单一化到多元化。数据库也随着整体信息化的推进不断吸收和融合新的理念与技术而发展，用户可以更加便捷地在数据库中查询所需信息。因果关系研究也是计算机科学领域的研究热点之一，因果关系是对问题更加本质的认识，比如在物理学、心理学或行为学中许多研究的核心问题是对因果关系的阐述，即对变量或事件之间直接作用关系的阐述[1-2]。

结构化查询语言(Structured Query Language, SQL)是用于访问和处理数据库的标准查询语言，在关系型数据库的查询中为用户提供方便高效的接口，且允许嵌套查询，有极强的可扩展性。常用的SQL查询有等值连接查询、不等式连接查询等，其中带有不等式查询条件的SQL连接查询(Queries with Inequalities, IQ)是应用较为广泛的一类查询，Dan等定义了一类不等式查询语句，并根据不等式查询条件的结构特性将其分为三类：路径类型、树类型和图类型[3-4]查询。因树类型、图类型的查询可拆分为若干路径类型查询，因此本文所提出的问题及方法均只针对带有不等式连接条件的路径类型查询(以下简称路径类型IQ查询)。

近年来，有学者创造性地将因果关系研究与数据库SQL查询结合研究，基于干预的思想，分析表中的元组对某个查询结果的因果关系。在查询中，如果某些数据库元组被删除，将会对查询结果产生较大影响。resilience[5]是一个将因果关系与数据库SQL查询结合研究的典型应用，根据resilience的定义，在查询中若删除最小个数的元组，查询将不成立时，此最小元组集合即为resilience解。通过resilience的量化描述，人们可以更充分地理解查询语句的因果性质，以及更好地知道在查询中哪些元组是对查询成立起决定性作用的元组，透过表象的数据，深层次地理解输入元组与结果之间的因果关联，以便更准确和高效地预测和干预查询。

文献[5-6]中研究了等值且无环连接查询的resilience计算，将其转化为最大流最小割问题，并理论证明其可以在多项式时间内完成，时间复杂度为O(VE2)(其中：V表示图中顶点的个数，E表示图中边的个数)，但未给出具体实现方式。在本文的研究中发现，最大流最小割方法不仅可处理无环等值连接查询，也可求解本文研究的路径类型IQ查询；但在大数据集合中，该算法复杂度较高，时间开销巨大，尤其是在不等式连接查询中，最坏情况下连接边E的数量接近O(V2)，算法时间复杂度约为O(V5)，巨大的时间开销无法满足用户的实时查询需求。

为了有效地计算路径类型IQ查询语句的resilience，本文首先实现了基于最大流最小割的算法(以下简称Min-Cut算法)；接着基于路径类型IQ查询连接图的特点，采用溯源表达式并将其编辑为溯源图，提出一种能够在线性时间复杂度内求解resilience的动态规划(Dynamic Programming for Resilience, DPResi)算法。相比最大流最小割算法，在路径类型IQ查询中计算resilience的时间复杂度由O(VE2)减小到O(V)，说明DPResi是一种高效可扩展的算法。

1 相关研究工作

1.1 不等式查询

本文主要研究的是数据库中带有不等式连接且每个表中仅有一个属性参与连接的路径类型查询语句，借鉴概率数据库研究中常用的查询语句的溯源表达方式[7-9]，将查询结果采用溯源表达式的方式来表示。

图1描述了示例数据库，其中共包含5张表，下文中所用算法示例都基于此示例数据库。

图1 示例数据库

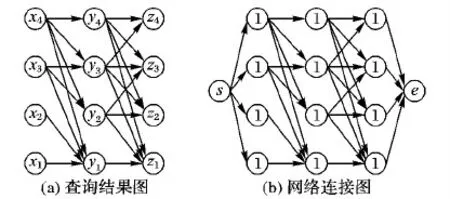
表1描述了基于图1示例数据库的IQ查询及其对应的查询结果溯源表达式。乘号代表一条连接边，加号代表整个查询的多条边，通过交换律和结合律，即可化简溯源表达式。例如Q3查询对应的溯源表达式为x4e1(f1+f2)，包含了两个合取子句x4e1f1和x4e1f2，这两个合取子句反映了查询中表之间元组的连接关系。图2(a)是Q2的查询结果，图3(a)是其对应的溯源图。以<为例，如果存在查询条件A

表1 查询语句及其溯源表达式

1.2 因果关系及resilience研究

因果关系是人工智能领域的研究热点之一，对于理解事件本质、起因有着重要作用。Galles等[10]提出了因果关系模型；Halpern[11]基于结构化的方程语言给出了因果关系的定义。类似于大多数因果定义一样，因果关系定义都是基于反事实定律的，当事件A是B的原因时，如果事件A没有发生的话，事件B也不会发生(然而事件A已经发生)。在文献[10-11]的描述中，世界是由随机变量所描述的，其中一部分变量可能会受到另外一部分变量的影响，这种影响可以通过结构方程式的方式所描述，每个方程式可能代表一种规定或条款等。这些变量通常可分为两类：外在型变量和内在型变量。外在型变量通常只由因果关系模型以外的变量所影响；而内在型变量通常是由因果关系结构方程所描述的。基于Halpern定义的因果关系模型，Chockler等[12]提出了responsibility的概念，当事件A是事件B的原因时，定义当改变A中最少个数的变量(n个)时，事件B会有明显的影响，responsibility的值为1/(1+n)。Chockler等[12]研究了responsibility时间复杂度，并证明在通常情况下，responsibility的计算是NP难问题；Meliou等[6]将responsibility与SQL查询相结合，研究了数据库中无环等值连接查询的responsibility计算，并证明了非线性查询语句的responsibility计算是NP完全问题，但线性查询的responsibility计算可以在多项式时间内完成。

resilience[5]是与responsibility意义相近的另一个因果关系的概念，定义为：当事件A是事件B的原因时，若删除A中最小个数的变量时，事件B将不成立。应用于数据库连接查询时表述为：在连接查询中，当删除表中最小个数的元组时，连接查询将不成立。Freire等[5]将resilience与responsibility作类比，提出了等值无环连接查询中求解resilience的方法，通过在连接结果图中增加起点和终点，将问题转化为在有向无环连接图中，割断最少个数的边使起点与终点间不连通。运用最大流最小割理论，提出使用Ford-Fulkerson算法求解，并理论证明了可以在多项式时间内完成，但没有给出具体实现，且没有扩展到其他类型查询。然而在本文的研究中发现，Ford-Fulkerson算法可计算路径类型IQ查询的resilience，但其具有多项式时间复杂度，时间开销较大，不适合处理大规模数据集。

1.3 最大流最小割算法

Ford-Fulkerson方法是Ford等[13]于1958年提出的增广链算法，是计算网络流的最大流最小割的贪心算法。Edmonds-Karp算法[14]是一种Ford-Fulkerson的实现，该算法的主要思想是只要有一条由起点到终点的连通路径，且在所有边上都有可用容量，就沿着这条路径发送一个流；然后再找到另一条路径，直到网络中不存在这种路径为止。该算法时间复杂度为O(VE2)。

2 resilience求解算法

本章首先分析路径类型IQ查询的连接图，给出了基于最大流最小割方法实现的Min-Cut算法，进而提出了本文的核心算法——DPResi算法，该算法主要分为两部分：溯源矩阵构造和最短距离计算。最短距离计算是充分利用了IQ查询溯源图的最优子结构性质而实现的动态规划算法，是一种O(V)时间复杂度的高效算法，具有很好的鲁棒性和可扩展性。

2.1 Min-Cut算法

通过最大流最小割算法描述，基于图2(a)对查询结果图增加起始点和终点，并将每个节点值置为节点内元组个数，表示该节点权重，得到图2(b)网络连接图，将问题转化为在图2(b)中求解起点s到终点e的最大流最小割问题。

图2 Q2的查询结果图及网络连接图

在路径类型IQ查询中，不等关系可包含多个元组的连接关系，即：xi元组可能与多个yi元组连接，因此在流式网络中，切割其中一条连接边没有意义，只有将xi删除，xi连向y列的连接才会失效，对应到网络连接图中，即置所有连接边的容量为无穷，切割时删除点xi。

标准的最大流最小割算法中网络流的容量在图的边中迭代，路径的距离为路径中边的权重相加，本文提出两种对连接图改造以适配Ford-Fulkerson的方法。

方法1 拆点成边，将点拆分为一条边，点的权重拆分成一条边上的权重，拆分后可直接使用最大流最小割方法。

方法2 修改算法中计算流大小的方法，将计算边权重改为计算点权重，即：f(xi→yi)=weight(xi)。

通过上面的描述，可简单地对标准Ford-Fulkerson算法进行改造，即可实现路径类型IQ查询的resilience计算的Min-Cut算法，具体算法如下所示。

输入：图G=(V,E)，源点s以及终点e。

输出：网络f中从s到e的最大流。

对于图中每一条边(u,v)，在开始时流量f(u,v)=0

当Gf中存在一条从s到e的路径p使得对于每一条边(u,v)都有cf(u,v)>0时

找出cfp=min{cf(u,v):(u,v)∈p}

对于p中每一条边(u,v)

f(u,v)=f(u,v)+cfp

f(v,u)=f(v,u)-cfp

在图2(b)的有向图中，运用Min-Cut算法可得出s到e的最小割为3，其中一个最小割集合为{x4,x3,y1}。当删除该最小割集合中的所有元组时，此查询将不成立，因此此查询的resilience解为3。

Min-Cut算法的空间复杂度与图存储数据结构有关，当采用邻接矩阵存储图时，空间复杂度为O(V2)；当采用邻接表存储图时，空间复杂度为O(E)，时间复杂度为O(VE2)。随着数据量增大或连接图变得相对复杂时，时间复杂度呈多项式增加，尤其是在不等式连接查询中，连接图中边数较多。给定N个表连接，平均每个表有M个元组，连接图中顶点数V约为MN。最坏情况下，连接图中的边数接近O(NM2)，采用Min-Cut算法的时间复杂度约为O(N3M5)。

2.2 DPResi算法

2.2.1 溯源矩阵

观察如图3(a)所示路径类型IQ查询的溯源图，通过聚合连接点，使得图中连接关系得以清楚地展示。数据结构中图的存储方式通常为邻接矩阵或邻接表，然而在溯源图中，每个节点均可连接至连接列的同行及以下的元素，例如图3(a)中x3可连接至y列同行元素y3及以下所有元素{y3,y2,y1}。这种包含连接关系使得可以使用矩阵形式存储该图，对应图3(b)所示溯源矩阵图，使用M×N的矩阵存储，本文称之为溯源矩阵(Lineage Matrix, LM)。

图3 Q2的溯源图及溯源矩阵图

定义1 孤立点与非孤立点。定义在溯源矩阵LM中，不存在的点称之为孤立点，并将其填充为0。其他所有点称为非孤立点，将其填充为对应节点内元组的个数。

在图4(a)所示溯源矩阵中，LM[0][2]、LM[2][0]为孤立点，故其值等于0。任意一个元素LM[i][j]可连接LM[i][j+1]至LM[M-1][j+1]的所有非孤立点。

通过如上描述，将IQ查询溯源图存储为一个结构清晰的矩阵，在算法实现过程中，仅需存储一个如图4(a)所示M×N的二维数组矩阵即可。图中边的关系，均可通过溯源矩阵自动获取，减少了邻接矩阵或邻接表存储边的开销，降低了算法的空间复杂度。其中：SDM(Shortest Distance Matrix)为最短距离矩阵。

图4 Q2的溯源矩阵及SDM

2.2.2 resilience求解

原SQL查询是自左向右进行连接，且由于IQ查询时，连接列具有有序的包含关系，以小于为例，自上向下降序排列，因此得出如下定理。

定理1 如果查询溯源矩阵图中左上角元组LM[0][0]到右下角元素LM[M-1][N-1]不连通，则查询不成立。

证明 反证法证明上述定理，假设查询成立。

在SQL查询中，查询成立时至少存在一条从最左侧连接列(x列)中元组LM[i][0]到最右侧连接列(z列)中元组LM[j][N-1]的连通路径。又因IQ查询具有包含关系，在构造的溯源矩阵图中LM[0][0]到LM[i][0]间必然存在一条连通路径。同理，LM[j][N-1]到LM[M-1][N-1]间也必然存在一条连通路径，即存在LM[0][0]到LM[M-1][N-1]的一条连通路径。而由定理1的条件所知，LM[0][0]到LM[M-1][N-1]不连通，所以假设不成立，定理1得证。

基于上述分析，依据resilience的定义，在IQ查询中，当最小个数的元组被删除时，查询不成立。将其转化为溯源图中描述即为，当删除溯源图中左上角元组至右下角元组最短连通路径上的节点后，查询将不再成立，即：路径类型IQ查询的resilience解为其溯源图中左上角元组LM[0][0]到右下角元组LM[M-1][N-1]的最短距离，最短距离结果存储在最短距离矩阵(SDM)中。

定理2 记LM[i][j]到LM[m][n]的距离为cost(LM[i][j],LM[m][n])，对于同行相邻元组之间有：cost(LM[i][j-1],LM[i][j])=0，对于同列相邻元组之间有cost(LM[i-1][j],LM[i][j])=LM[i][j]。

证明 在溯源矩阵图中，对于任一非孤立点LM[i][j]，最多有两条通路可达。依据溯源图的构造规则，每一条自左向右的连接为溯源表达式中一条合取子句，代表连乘操作。当左侧节点LM[i][j-1]不连通时，当前单条合取子句将不成立，此时自左向右连接的距离cost(LM[i][j-1],LM[i][j])=0。每一条自上向下的连接为溯源表达式的合取子句相加操作，需删除LM[i][j]才能使该溯源表达式不成立，即溯源图不连通，因此自上向下连接的代价cost(LM[i-1][j],LM[i][j])=LM[i][j]。

定理3 对于LM右上角存在的孤立点，在SDM中，将对应的位置置0。

证明 当LM右上角存在孤立点时，因其元组不存在，从LM[0][0]到这些孤立点的子连接查询本身就不存在，故此时，LM[0][0]到这些点的距离为0。

Dijkstra算法是求解单源最短路径较为经典和高效的方法[15]，复杂度为O(V2)，然而观察溯源矩阵图，具有明显最优子结构性质，具备如下的递归特性。

递归1 置SDM[0][0]=LM[0][0]，对首行顶点，SDM[0][j]=min(SDM[0][j-1],LM[0][j])(0

递归2 对第一列中的顶点，SDM[i][0]=SDM[i-1][0]+LM[i][0](0

递归3 对其他顶点LM[i][j](0

通过上述递归分析，提出了本文的核心算法——DPResi，如下所示。

输入：LM[M][N]。

输出：SDM[M][N]。

for (i=0;i

if (LM[i][N-1]≠0) break

for (j=N-1;j>=0;j--)

if (LM[i][j]=0)SDM[i][j]=0

else break

SDM[0][0]=LM[0][0]

for (j=1;j

SDM[0][j]=min(SDM[0][j-1],LM[0][j])

for (i=1;i

SDM[i][0]=SDM[i-1][0]+LM[i][0]

for (i=1;i

for (j=1;j

SDM[i][j]=min{SDM[i][j-1],

SDM[i-1][j]+LM[i][j]}

在图4(a)中运用DPResi算法，可以计算出该示例查询对应的SDM结果矩阵，如图4(b)所示。SDM[3][2]为该示例的resilience解，即至少删除3个元组，此查询将不成立。通过回溯SDM即可得到需要删除的元组集合，如图4(b)中的回溯路径，对应到LM中得到其中一条回溯路径为LM[3][2] →LM[3][1] →LM[2][1] →LM[2][0] →LM[1][0] →LM[0][0]，即每行仅需删除最左侧元组后，该行将不成立，且去除孤立点，结果集合为{LM[3][1],LM[1][0],LM[0][0]}对应图3(a)所示溯源图中原始元组集合为{x4,x3,y1}。

2.2.3 DPResi算法复杂度分析

路径类型IQ查询语句在计算resilience时，对于原始查询图，由于不等关系的存在会导致结果图中存在较多的边，在M×N的连接图中，边的个数约为O(NM2)。而通过溯源表达式及溯源图的表示，将路径类型IQ查询的包含关系表示为矩阵的形式，逻辑意义上的连接边数为O(MN)。在现在的大数据时代，数据库中行数通常可能是百万级或者更多，连接查询时，连接表个数通常是较少的，即M≫N。溯源图将图复杂度降低了一个数量级，且通过溯源矩阵替代邻接表或邻接矩阵存储图，仅需O(MN)的空间复杂度。

DPResi算法时间复杂度也为O(MN)，一趟扫描LM即可得到SDM最短距离矩阵。矩阵中SDM[M-1][N-1]的值代表左上角元组LM[0][0]到右下角元组LM[M-1][N-1]的最短距离，即为此查询的resilience解，通过回溯SDM，可求得需要删除的元组集合。基于溯源图求解resilience的算法时间复杂度与溯源矩阵图中顶点个数V呈线性关系，易于扩展到大规模数据集上，是扩展性非常好的算法。

3 实验对比

实验在Windows系统下进行，系统配置：内存为8 GB，CPU为Intel Core i7- 4790@ 3.60 GHz，数据库为PostgreSQL 9.0。DPResi算法及Min-Cut算法由C++语言编程实现，数据集采用的是TPC-H。

查询语句 实验主要对比带有不等式关系的路径类型查询语句的resilience计算时间开销，因此，随机选择了4组路径类型IQ查询语句用于性能对比，且为了覆盖不同类型、不同量级的查询，这4组不等式查询语句所包含的节点个数及元组都不尽相同。其中每组查询包含4条具有不同过滤条件的查询语句，算法时间开销主要与连接元组总个数V有关，因此通过过滤条件的不同来控制查询所产生结果的元组数量(1X代表基准查询语句，2X、5X、10X分别代表结果元组数为基准的2倍、5倍、10倍)。表2列出了1X大小下的4组查询语句，表3列出了实验用到的16条查询语句的查询结果元组量。

在本文前面描述中，理论分析了DPResi算法与Min-Cut算法的时间复杂度，可知Min-Cut算法O(VE2)的时间复杂度远远超过了DPResi算法O(MN)的时间复杂度。在实验中，本文首先实现并验证了Min-Cut算法的可行性，且为了验证DPResi算法的高效性及可扩展性设计了对比实验进行验证。实验结果如图5所示，其中：横轴表示查询结果元组的量级，纵轴表示resilience计算所需时间(单位μs)。

表2 实验查询语句

表3 查询的数据规模

对于路径类型IQ查询语句，通过图5可知，在不同查询中，DPResi算法时间开销均远远低于Min-Cut，且DPResi算法时间开销随数据规模增大而线性增加，而Min-Cut算法呈多项式增长。如Q7在10X的数据量级下，查询结果元组数约为2.50×107，DPResi算法时间开销仅779 μs，与Min-Cut算法72 s的时间开销相比，耗时仅为Min-Cut算法的1.07×10-5，降低了99.99%。时间开销差距较大，性能优势明显，DPResi算法对于路径类型IQ查询语句resilience计算具有较高的效率，尤其在当前信息爆炸的时代，其线性时间复杂度的开销能够处理大规模数据集，有极好的可扩展性。

图5 两种算法的时间开销对比

4 结语

本文提出一种对带有不等式连接的路径类型查询语句进行因果关系resilience计算的DPResi算法，通过将查询的溯源表达式编辑为溯源图，有效地完成了路径类型IQ查询语句的resilience计算，进而更深层次地对所看到的查询结果作出解释，也便于人们对当前SQL查询进行干预。本文通过与现有的Min-Cut算法对比，验证了DPResi算法能够极大地降低计算的时间开销，提升resilience计算效率，且能够较好地扩展到大规模数据集上。在接下来的研究中，可将resilience计算由路径类型扩展到树类型及图类型的查询中，并提出更高效的算法来解决带有等值连接与不等关系连接的混合查询语句resilience计算的问题。