基于竞争学习的稀疏受限玻尔兹曼机机制
2018-08-27周立军吕海燕
周立军,刘 凯,吕海燕
(海军航空大学 航空基础学院,山东 烟台 264001)(*通信作者电子邮箱jungle730@163.com)
0 引言
目前,以受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)为基础的深度学习模型已经广泛应用于数据维度处理[1]、图像处理[2]、文本检索[3]以及时间序列预测分析[4]等机器学习领域。
RBM的训练为无监督训练方式,此类训练存在的重要问题是学习特征的同质化[5-6],即RBM易受训练数据维度间共有因素的影响,导致提取的特征过于相似,从而影响模型对数据的泛化能力。为抑制这一问题,通常采用两种方法。一种是改进模型结构。如:文献[7-8]将类别信息引入模型中,设计了三阶受限玻尔兹曼机;文献[9]在RBM的基础上增加了部分可见单元间连接,从而抑制数据共有特性;文献[10]设计了网络结构的随机衰减机制(dropout);文献[11]在dropout随机网络结构基础上进一步提出了多RBM组合模型,这类方法通过训练数据额外信息的加入,抑制数据维度间同有特性的影响,但存在的问题是,结构的优化多以特有模型为基础,对于其他无监督训练方式模型较难适用。另一种是设计优化策略优化模型训练过程,优点为优化策略易推广至其他无监督训练模型,具有一定的适用性。例如文献[12-14]将模拟退火、遗传算法等全局优化方法引入到RBM等无监督训练中的吉布斯采样内,改善模型训练效率。文献[15-19]对训练目标进行优化,引入多种正则化因子:文献[15]限定隐单元平均激活概率与稀疏度系数的2范数;文献[16]提出基于交叉熵的稀疏惩罚因子;文献[17]通过设计隐单元激活概率的1- 2范数组合对隐单元进行分组稀疏;文献[18]对文献[17]进行扩展,增加范数混合因子以调节RBM组内外稀疏度;文献[19]对稀疏组受限玻尔兹曼机的单元分组进行研究,设计了基于连接权值相似度的隐单元分组策略。上述正则化因子通过稀疏隐单元激活概率,从而弱化训练过程的数据共有特性影响,以提高模型泛化能力;但存在的问题是,额外增加的模型训练参数往往需要通过经验进行设置,不能依据训练过程中的隐单元稀疏程度进行自适应调整,导致模型训练效率不高。
基于竞争的自组织映射网络(Self-Organizing feature Map, SOM)能够通过其输入样本学会检测其规律性和输入样本相互之间的关系,并且根据这些输入样本的信息自适应调整网络,并可通过与其他模型结合对其训练进行指导[20-21]。文献[20]提出将SOM引入拓扑地图制作中,减少了网络的训练次数,降低了系统复杂度;文献[21]将脉冲神经网络的高效处理能力与自组织映射神经网络相结合,大幅度缩短了脉冲神经网络网络训练时间。本文以SOM的竞争机制为基础,借鉴SOM网络中最优神经元对其他神经元的抑制作用,提出依据RBM中隐单元相关性对其进行自适应稀疏惩罚的方法,由此设计了基于竞争的稀疏受限玻尔兹曼机(Competition-Sparse Restricted Boltzmann Machine, C-SRBM),并应用于深度玻尔兹曼机(Deep Boltzmann Machine, DBM)训练中。实验表明,相比以往的正则化因子,C-SRBM能够进一步优化RBM,并可有效应用于深度模型的构建。
1 稀疏受限玻尔兹曼机及竞争学习
1.1 受限玻尔兹曼机及稀疏受限玻尔兹曼机
RBM是通过限定玻尔兹曼机(Boltzmann Machine, BM)层内单元连接构成的双层神经网络。作为无向图模型,RBM中可见单元层V为观测数据,隐单元层H为特征检测器,其结构如图1所示。

图1 RBM单元连接图
设定RBM包含N个二值可见单元和M个二值隐单元,给定状态(v,h)下的模型能量定义如式所示:
(1)
其中:vi代表第i个可见单元状态,hj为第j个隐单元状态,Wij表示可视单元i与隐单元j之间的连接权值,bi表示可视单元i偏置,cj表示隐单元j偏置。
稀疏受限玻尔兹曼机(Sparse Restricted Boltzmann Machine, SRBM)优化了RBM的训练目标,即在RBM最大似然目标函数的基础上增加了稀疏惩罚因子,因此,SRBM的训练目标函数如式(2)所示:
(2)
其中:N为训练样本个数,λ为用于控制稀疏度惩罚因子影响的正则化常量,v(n)代表第n个训练样本,PE表示稀疏惩罚因子,P(v(n))为v(n)的条件概率。
从式(2)可看出,SRBM中隐单元的稀疏化,是在RBM训练过程中通过叠加稀疏惩罚因子,以此激励隐单元平均激活概率接近稀疏度p实现的。SRBM对隐单元的稀疏性进行调节,迫使仅部分隐单元用来表示训练样本,从而减少数据维度间共有特性对隐单元的影响,以提高模型的特征学习能力。
1.2 竞争学习
竞争型神经网络有很多具体形式和不同的学习算法,但最主要的特点体现在竞争层中神经元之相互竞争,最终只有一个神经元获胜,以适应训练样本。
SOM网络是竞争型神经网络的中应用较为广泛的一种。SOM网络能够自动找出训练数据间的类似度,并将相似的数据在网络中就近配置,其训练步骤可归纳如下:
1)网络初始化。
使用随机数初始化输入层与映射层之间的连接权值W。
2)计算映射层的权值向量和输入向量的距离。
计算网络中各神经元权值向量和输入向量之间的欧氏距离,得到具有最小距离的神经元j,作为最优神经元。
3)权值学习。
依据最优神经元,对输出神经元及其邻近神经元权值进行修改,如式(3)所示:
ΔWij=Wij(t+1)-Wij(t)=η(Xi(t)-Wij(t))
(3)
其中:Wij(t)为模型训练第t次迭代中输入层单元i与映射层单元j之间的连接权值,η为模型学习梯度系数,Xi(t)为第t次迭代中单元i对应的训练数据。
2 基于竞争的稀疏受限玻尔兹曼机
针对以往正则化因子不能依据训练过程中的隐单元稀疏程度进行自适应调整的缺陷,提出C-SRBM以提高隐单元稀疏程度,提高模型训练效率。
2.1 基于竞争的稀疏惩罚机制
C-SRBM采用了类似于SOM网络的神经元竞争机制对隐单元进行稀疏化。在模型训练过程中,C-SRBM首先依据训练样本选择最优匹配隐单元,然后依据最优匹配隐单元激活状态对其他隐单元进行稀疏抑制,最后执行参数更新,具体机制如下所示。
1)距离度量。
RBM将原始数据通过模型连接权值由原始维度空间映射至多维0- 1空间,样本所生成的0- 1序列即为对应的多特征组合。鉴于RBM模型连接权值为可见单位维数×隐单元维数,即连接权值的列数等于隐单元个数,且连接权值与样本在单位刻度上并不一致,因此,C-SRBM没有采用SOM网络常用的欧氏距离作为度量标准,而是选用神经元权值向量与输入向量之间的夹角余弦值评估两者相似度,即样本i与隐单元j之间余弦相似度Scos(i, j)的计算方法如式(4)所示:
(4)
其中:v(i)代表第i个训练样本,W·j为模型连接权值的第j列。
2)最优匹配隐单元选取。
依据样本i与所有隐单元之间的余弦相似度,可确定针对样本i的最优匹配隐单元,即与样本i相似度最高的隐单元hcos-max,如式(5)所示:
Scos(i,hcos-max)=Fmax(Scos(i, j));j=1,2,…,M
(5)
其中:M为隐单元个数,Fmax为寻找最大值函数。
3)最优神经元稀疏抑制。
C-SRBM根据最优神经元状态设置其他单元的稀疏化程度。最优神经元的稀疏抑制依据连接权值列间的余弦相似度,其过程为:
①计算对应于最优隐单元的连接权值列W·cos-max与W其他列的余弦相似度,得到相似度向量Scos;
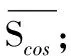

2.2 C-SRBM训练流程
RBM的训练为无监督训练,其目标为最大化训练数据出现的似然概率,采用的训练方法为对比散度(Contrastive Divergence, CD)算法。C-SRBM的竞争稀疏机制对参数W.j和隐单元偏置bj的更新如式(6)~(7)所示:
(6)
(7)
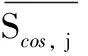
综上所述,C-SRBM训练的伪代码如下所示。
输入:学习速率η,网络连接权值W,可见单元偏置c,隐单元偏置b。
输出:更新后的W,b,c。
训练步骤如下。
1)依据CD算法更新W,b,c:
wij=wij+η(〈vihj〉data-〈vihj〉recon)
ci=ci+η(〈vi〉data-〈vi〉recon)
bj=bj+η(〈hj〉data-〈hj〉recon)
2)依据式(5),查找当前样本p最优匹配隐单元hp。
3)应用式(6)、(7)计算并依据最优神经元稀疏抑制流程更新W,b:
wij=wij+ηΔW.j
bj=bj+ηΔbj
4)重复步骤1)~3)直至模型收敛或者超过训练迭代次数。
2.3 深度玻尔兹曼机训练设计
深度玻尔兹曼机(Deep Boltzmann Machine, DBM)和深度信念网络(Deep Belief Network, DBN)是两种常见的以RBM为基础的深度学习模型,其共同特点为类似人脑的信息处理机制和多个RBM叠加组成的结构体系。
考虑到DBM和DBN训练过程中,首先完成的是叠加RBM的贪婪逐层初始化训练,因此将C-SRBM的稀疏惩罚机制引入到深度学习模型训练中,形成基于竞争的稀疏深度学习模型。以DBM为例,本文将C-SRBM应用于DBM的构建中,组成基于竞争的稀疏深度玻尔兹曼机(Competition-Sparse Deep Boltzmann Machine, C-SDBM),并进行实验验证。
小行星撞击地球的过程如图12所示。在能够对近地小行星提前预警的前提下,将小行星分裂成碎片或者改变小行星轨道是避免其撞击地球的两种基本方式。根据防御技术的作用时间以及目标小行星尺寸的不同,安全防御技术可分为3大类[38-39]:1)利用核爆炸摧毁小行星或者改变行星轨道,防止尺寸较大且预警时间较短的PHAs撞击地球;2)利用航天器直接撞击小行星改变其轨道,此方法适用于防御尺寸较小且预警时间较短,或者尺寸较大且预警时间较长的PHAs;3)利用长期作用力改变小行星轨道,通过接触式或非接触式作用使小行星产生微小速度变化,随着时间推演进而演化为极大的轨道变化。
3 实验结果及分析
实验采用MNIST手写体字符识别数据集作为模型训练对象,该数据集共包括70 000幅0~9的10种手写数字图像,图像大小统一为28×28[22]。在实验中,随机选取MNIST数据集中60 000幅图像作为模型训练样本,其余图像用于测试。为验证C-SRBM稀疏性能,实验包含2个部分,分别为单层RBM稀疏实验和深度模型DBM稀疏实验。
3.1 单层RBM稀疏实验
为有效测试不同正则化因子对RBM特征提取能力的影响,从两个方面进行实验对比,分别为:1)相比其他正则化因子,检验C-SRBM是否能够优化模型特征提取能力;2)验证C-SRBM在增强隐单元稀疏度上是否优于以往正则化因子。
实验设置:设定RBM中可见单元个数为784,参数的学习速率统一为η=0.01,循环次数K≤1 000,p=0.01;完成手写字特征提取以后,采用LIBSVM[23]提供的径向基支持向量机(Radial Basis Function-Support Vector Machine, RBF-SVM)和线性支持向量机(Linear Support Vector Machine, LSVM)作为最终分类器,其中参数设置除核函数不同外,其余均为默认选择。
3.1.1 实验1
设定不同的隐单元个数M,分别计算在两种不同分类器下采用误差平方和、交叉熵正则化因子的SRBM与C-SRBM的分类准确率δ,其变化曲线如图2所示。
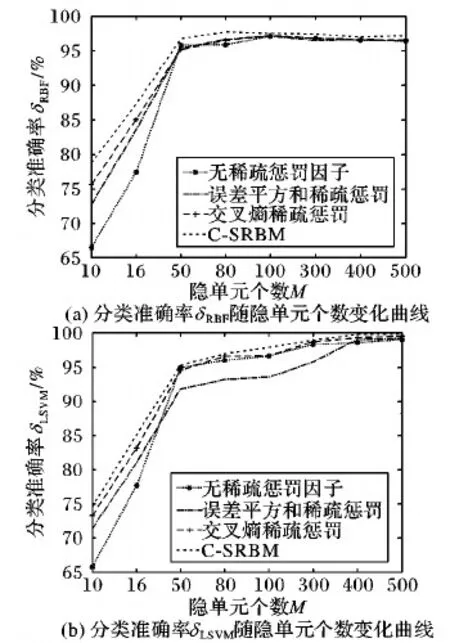
图2 分类准确率随隐单元个数变化曲线
3.1.2 实验2
为直观显示不同正则化因子对DBM特征的影响,对RBM的连接权值进行可视化显示。设置本实验M=16,对这16个1×784的列向量进行变维,并将所得到的方块矩阵依次排列。
经过训练后的标准RBM、误差平方和稀疏RBM、交叉熵稀疏RBM和C-SRBM的连接权值可视化显示,如图3所示。

图3 RBM连接权值可视化显示
从图3中可以看出:图3(a)的左列特征图像基本一致,且很难发现其中的笔画特点,类似于白噪声图像,表明该列对应的4个隐单元对手写数字无效,无法完成训练数据的特征提取;图3(b)和图3(c)仍然存在特征图像笔画特点模糊以及若干图像相似的问题;相反的,图3(d)中特征图像差异较大,且没有出现类似于图3(a)~(c)中接近于高斯白噪声的图像。这说明,相较于其他2种正则化因子,竞争稀疏机制对RBM特征的稀疏程度较好。
结合实验1结论,可以说明,采用竞争稀疏惩罚机制构建的C-SRBM在特征提取能力和隐单元稀疏度上均优于以往2种正则化因子。原因在于,C-SRBM能够依据RBM训练过程中隐单元激活状态自适应调整稀疏惩罚力度,即随着模型对数据拟合程度增强,最优匹配神经元与样本间的相似度越高,从而增强对其他隐单元的稀疏抑制,加深了隐单元稀疏程度,进而弱化了特征同质化问题并提高了模型提取特征的有效性,最终C-SRBM的分类准确率得到提高。
3.2 深度模型DBM稀疏实验
在DBM稀疏实验中,主要验证C-SRBM是否能够提高DBM模型性能,因此,本实验中DBM模型选用文献[24]提出的网络结构,即设置C-SRBM初始化可见单元个数784,中间隐单元个数500,顶层隐单元个数200的DBM网络。待完成DBM的贪婪逐层初始化以后,使用BP算法对网络参数进行精调,其分类准确率δ如表1所示。

表1 不同DBM的分类准确率δ %
从表1可以看出,使用C-SRBM优化的DBM分类准确率最高,达到99.75%,与文献[15]依据误差平方和稀疏惩罚因子优化的稀疏DBM相比,提高了0.74%;与文献[24]标准DBM准确率相比,提高了0.9%。为比较三种不同稀疏惩罚机制对隐单元稀疏程度的影响,选取Hoyer提出的稀疏度度量HSparse[25]。对于D维向量v,HSparse如式(8)所示:
(8)
从式中可以看出,HSparse区间范围为[0,1],且值越接近1代表向量v越稀疏。
结合实验1过程,3种DBM所有隐单元构成的特征向量HSparse在测试集上的平均值如表2所示。

表2 不同DBM的平均稀疏度度量HSparse
从表2可以看出,C-SDBM的隐单元稀疏程度最好,其次是文献[15]优化的稀疏DBM,HSparse数值最低的为标准DBM。使用C-SRBM优化的HSparse最高,与依据误差平方和稀疏惩罚因子优化的稀疏DBM相比,提高了5.6%;与标准DBM相比,提高了6%。结合表2数据可以证明,C-SRBM能够进一步稀疏优化深度学习模型,并提高模型的特征提取能力。
4 结语
本文采用基于竞争学习的受限玻尔兹曼机稀疏机制,实现了弱化模型特征同质化和提高模型数据特征提取能力的目标。相对于以往正则化因子,采用竞争学习策略,从而无需设置额外的稀疏系数,并且能够在RBM训练过程中自适应地调节单元稀疏化惩罚程度,提高了模型训练效率;与此同时,将其成功应用于深度模型DBM训练中,表明基于竞争学习的RBM稀疏化对其他以RBM为基础的深度学习模型也具有良好的应用前景。
