基于线性松弛方法的网络故障链路诊断

范晓波，李兴明

(电子科技大学 通信与信息工程学院，成都 611731)(*通信作者电子邮箱xiaobof@outlook.com)

0 引言

网络中的链路故障会导致终端用户的连接中断，因而快速、准确地定位网络内部的故障链路对于维护网络性能、提升网络服务质量有着重要意义。除了物理链路的故障，一些如路由器配置错误等“软”的错误也会导致连接失败[1]。最简单、直接的诊断故障链路的方法是通过网络内部节点间的协作直接监测链路性能参数，但是出于安全因素的考虑，内部节点通常不协作，因此直接监测的难度较大。近年来，网络层析(network tomography)技术[2-3]在网络推理中得到了广泛的应用。网络层析技术可以在没有中间节点协作的条件下，通过主动发送端到端探测包或被动收集有用的信息来估计网络内部性能参数。由于其仅需要在网络边缘进行端到端测量，无需内部节点的协作，适用于复杂网络环境，同时其可扩展性强，因而受到了广泛的关注。

采用网络层析技术识别故障链路的思路最早由Coates等[2]和Padmanabhan等[4]提出。其思路是选择一些路径，然后通过在这些路径上主动发送端到端探测包来识别故障链路。对于每一条路径，当且仅当路径上的任意链路出现故障时，整条路径就会失败。由于只有两种状态，这种层析技术也称为布尔层析[1,5-8]。布尔层析将链路和路径的状态看作是布尔型的，其中0表示正常和1意味着失败，而链路和路径的状态在布尔代数[6]中是线性相关的。然后将布尔层析成像看作是一个优化问题，即找出最小的链路失效集，以解释所测量路径的状态。然而，求解此类优化问题一般是NP(Nondeterministic Polynomial)难的，因此，当前研究中普遍采用贪婪启发式算法。在文献[1]中提出了一种TOMO(TOMOgraphy)方法，该方法迭代地选择那些能解释最多失效路径的链路当作故障链路。文献[6]提出了一种类似的方法CLINK(Congested Link identification)，该方法可以看作是将链路的故障先验概率作为权重的TOMO加权版本，并提出了一个使用多种测量时隙联立方程来学习这些概率的方法。类似文献[6]，文献[7]提出一种基于因子图—和积方法来估计先验概率。然而，由于先验概率的估计总是需要多个测量时隙，在实际应用中受限。此外，文献[8]研究了在布尔层析中使用不同的端到端探测机制时定位故障的能力。

不同于已有的故障链路检测技术，受文献[9]和[10]中凸松弛法的启发，本文提出了一个简单而有效的线性规划(Linear Programming, LP)松弛方法来定位网络中故障的链路。该方法将链路状态的布尔约束松弛到连续区间，然后将问题转化为一般线性规划问题。

1 模型和框架

同大多数现有的基于端到端测量来推断网络内部性能研究类似，本文将一个无向网络建模为一个图G=(V,E)，其中：V表示网络中的主机或中间路由设备集合，E代表网络中的链路集合。为了监测网络中的故障情况，从V中选择一些节点集合M(M⊂V)作为测量节点，通过在测量节点之间发送和接收探测包得到路径测量信息，最后从路径的测量状态中推断出网络内部的链路状态(正常/故障)。

链路和路径的状态之间的关系可以表示为如下布尔代数模型。令布尔变量yl表示路径pl的状态，布尔变量xk表示链路ek的状态，并约定对于路径和链路，均用0代表正常、用1代表故障。由于当且仅当路径上的任意链路出现故障时，整条路径发送的探测包就会失败，因此链路状态和路径的状态有如下关系式：

记n为网络中的总链路数，根据上式，可以得到：

(1)

其中“∨”表示布尔代数中的OR操作，rlk取值为{0,1}，如果ek∈pl则rlk取值为1；否则取值为0。

不失一般性，假设网络中总共有m条测量路径，对于每一条测量路径，都有如式(1)的等式成立。为了简便起见，将这m个等式写成如下矩阵形式：

y=R⊙x

(2)

其中：y=(y1,y2,…,ym)T表示m条端到端测量路径的状态，x=(x1,x2,…,xn)T表示n条链路的状态，注意x，y均为布尔向量。R=[rlk]为一个m×n0- 1矩阵，由于其代表的含义为相关路径是否经过相关链路，因而又称为路由矩阵(routing matrix)。最后，式中的⊙为布尔矩阵中的相乘操作，y的每一项由式(1)所确定。

由于网络端到端的路由相对固定，因而链路故障检测即为给定R和路径测量y，求解式(2)中的布尔向量x。在实际测量中式(2)总是存在多个解。由于在网络中，出现故障的链路总是网络所有链路的很小部分，现有的网络层析技术将问题转换为找到一个最小的故障集合用来解释所有观测到的端到端路径结果[1]，这可用如下优化问题描述：

(3)

s.t.y=R⊙x,xi∈{0,1}

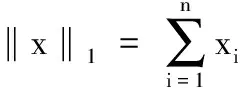
事实上，如果把网络里每条路径看作是链路集合，那么式(3)即是如下问题的数学描述：寻找最小的故障链路集合，使得该集合与每条故障路径都要相交，且和每条未发生故障路径(正常路径)都不能相交。该问题为最小碰集问题(Minimum Hitting Set)[11]的一个特例，由于最小碰集问题为著名NP难问题，因而求解优化表达式(3)是NP难的。现有的链路诊断研究普遍采用贪婪启发式算法[1,6-8]求解。大体来说，在每一次迭代，它们选择具有最大“分数”的那条链路作为故障链路，这里的分数通常被定义为通过链路的未被解释的故障路径数。

2 线性松弛方法

不同于已有的故障链路检测技术，本文提出了一个简单而有效的线性规划(LP)松弛方法来求解式(3)，从而定位网络中故障的链路。在线性松弛过程中分为两步来进行，首先将优化问题(3)等价变换为二元线性规划，然后松弛其自变量的二元限制得到常规线性规划。

显而易见，式(3)的优化目标是关于x的线性函数：

(4)

s.t.RJx=0,RIx≥yI,xi∈{0,1}

通过上述等价变换，得到的问题(4)实际上是一个二元线性规划(binary linear programming)，众所周知，也是一个NP难题。然而，通过松弛布尔限制xi∈{0,1}，可得到一个常规的线性规划：

(5)

s.t.RJx=0,RIx≥yI, 0≤xi≤1

由于式(5)为常规的线性规划，即使网络规模非常大，仍能得到有效的求解，譬如采用内点法[12]。

3 仿真和性能分析

3.1 仿真环境

为了验证本文方法的有效性，本文使用Matlab搭建仿真平台，测试了故障检测算法在不同的网络拓扑下的表现性能。实验网络拓扑采用Rocketfuel项目所测量的实际ISP(Internet Service Provider)骨干网络拓扑[13]：AS4755和AS7018，AS4755是一个小规模的网络而AS7018相对较大。对于每个网络，实验中选择边界节点(度为1的节点)作为测量节点。然后通过最短路径路由建立任意两个测量节点之间的测量路径。注意到有些链路可能没有被任何测量路径所经过。由于这些链路的状态始终不能被识别，故而删除这些链路。表1总结了实验中采用的修改后的网络拓扑和测量路径。

表1 实验中使用的网络拓扑

在每一次的仿真模拟实验中，从网络中随机挑选k%条链路作为故障链路，k值表示网络所遭受的故障级别。为了仿真在不同的故障级别下算法的性能，本文设定故障链路百分比为5%至30%。实验步骤简要总结如下：

1)选择网络拓扑AS4755或AS7018，并在网络中随机选择k%条链路视为故障链路；

2)在网络中的测量节点之间发送探测包，根据测量路径是否经过故障链路来判定探测包是否发送成功；

3)记I为发送失败的路径，J为发送成功的路径，然后求解线性规划式(5)得到链路状态向量x*；

同时为了验证所提出的方案的有效性，将所提出的线性松弛方法和启发式算法TOMO[1]进行了比较，TOMO被广泛运用于IP网络中的故障诊断。评价指标采用漏报率(False Negative Rate, FNR)和误报率(False Positive Rate, FPR)。FNR是指将故障链路错误的判定为正常链路的比率，而FPR是指将正常链路判定为故障链路的比率。其计算公式如下：

其中：Sa表示真正发生故障的链路，Sd表示算法检测到的故障链路。在检测理论中，FNR和FPR通常联合使用用来综合评估一个算法的有效性。

3.2 仿真结果

对于每次参数设定下的仿真结果，给出其500次实验的平均值。仿真结果显示在图1～2中，分别对应网络AS4755和AS7018。从图中可以看出线性松弛方法和TOMO方法具有类似的变化趋势，具体来说，随着链路故障数的增加，这两种算法的漏报率和误报率都越来越高。这是因为在存在很多个链路故障时，很难找到网络中所有的故障。从结果中还可以看出，检测故障链路主要的错误来源是漏报率(在大多数情况下，误报率都小于0.1)，也就是说，算法很容易忽略一个真正的链路故障，而不是错误地将一条正常链路识别为故障链路，这和文献[1]的结论是一致的。最后，从图1和图2可以看出，线性松弛方法比TOMO方法的漏报率要低，特别是当链路故障比例较高时。譬如，当故障链路比率大于20%时，从图中可以看出本文的线性松弛方法的FNR明显低于TOMO算法(对于拓扑AS4755约改善30%，拓扑AS7018约改善10%)。这一点也可从图3中得到验证，图3显示了在500次仿真中漏报率FNR出现的次数，设定实际故障链路数为3，因而漏报率取值范围为{0,1/3,2/3,1}。由图可见，线性松弛法大多数情况下漏报率为0，而TOMO方法出现高漏报率次数显然较多。综合实验结果分析可以得知，线性松弛方法在漏报率上要低于TOMO方法，而误报率两个算法都很小且近似相等(LP松弛法有极小幅增加)，证实了线性松弛方法的有效性。

图1 两种方法在AS4755的漏报率和误报率对比

图2 两种方法在AS7018的漏报率和误报率对比

图3 两种方法在AS4755中漏报率出现次数对比

4 结语

本文研究了如何通过端到端路径测量在通信网络中检测故障链路的问题。由于该问题是NP难的，本文采用一种直观有效的方法，即通过松弛变量的非凸布尔约束，将问题简单化为线性规划。在实际网络拓扑上对该方法的性能进行了评估，结果表明，与常用的贪婪算法相比，该算法具有更低的漏报率和可比的误报率。本文研究的是故障链路诊断问题，下一步工作重点将是拓展该方法，如何检测网络中特别是无线网络中的故障节点问题。