带式输送机阻力计算方法研究进展及存在的问题

◎ 郭金星，宋伟刚

（1.河南天隆输送装备有限公司，河南 新乡 453000；2.东北大学机械工程与自动化学院，辽宁 沈阳 110819）

带式输送机是最重要的散状物料输送设备，现代带式输送机由Thomas Edison在1891年设计，使用在新泽西的Ogden铁矿，一般认为，Robbins于1885年发明了带有槽形托辊的带式输送机[1]。最早出版的带式输送机设计的书籍可以追溯到Hetzel在1901年出版的Belt Conveyors and Belt Elevators[2]。带式输送机在粮食系统中的粮库和港口粮食物流中心也有广泛的应用。

20世纪50年代，在Vierling等[4]开展了大量的理论研究，得出了一些影响因素的回归计算式[3]。Vierling和Oehman对运行阻力的测量，确定了运行阻力的计算方法。在美国，1954—1956年间，经过对现场带式输送机的测试，给出了承载段阻力系数与承载重量的关系曲线，于1966年形成了CEMA传统计算方法[5]。1980年Jonkers[6]给出了压陷滚动阻力的计算方法，Spaans[7]、Lodewijks[8-9]研究了带式输送机主要阻力的计算方法，Nordell等[10-12]通过橡胶损耗模型的现场实测开展应用。Hager等[13-17]对输送机的运行阻力、接头强度曲线和过渡段的附加应力等开展研究，以1条1 km长的带式输送机为例，给出了带式输送机各种阻力的分布，形成了DIN22101-2002[18]、DIN22123[19]。邱向军提出全二维压陷滚动阻力模型[20-22]，并针对主曲线求解Prony级数参数困难问题，提出了避免求解Prony级数参数的QC-N模型。Rudolphi等[23-25]应用橡胶试样测得橡胶储能模量和耗散模量的主曲线，采用广义Maxwell模型计算压陷滚动阻力，该方法是CEMA[26-27]的计算基础。Wheeler等[28-39]研究了输送带的弯曲阻力、物料弯曲阻力、托辊转动阻力、输送带压陷滚动阻力，开发了托辊转动阻力和压陷滚动阻力实验台，其阻力的计算多采用有限元方法，所开发的压陷滚动阻力实验方法已经形成AS1334-13[40]。

1 压陷阻力产生的机理与主要问题

物料和输送带的重力将传递到托辊上，使托辊和作为抗拉元件的输送带骨架之间的输送带橡胶受到挤压。当输送带接触托辊组辊子表面时，挤压力引起输送带变形，会阻碍输送带的运动；当输送带通过托辊后，由于恢复作用，输送带受到的挤压变形减弱。由于橡胶是粘弹性材料，挤压变形的恢复存在时滞，变形功的一部分不能恢复。导致这部分变形能全部转化为热能而损耗，这可以看成由作用辊子中心和垂直反力中心之间的偏距产生的沿输送带运行方向的纯运动阻力，见图1。橡胶的性能可以由实验测得的主曲线来表示，见图2。由此可见，带式输送机输送带压陷阻力的计算可归结为具有粘弹性特性的输送带经过刚性辊子时压陷变形所产生的能量消耗所等价的阻力。其影响因素包括：输送带的下覆盖层厚度与辊子直径、环境温度与带速、覆盖橡胶的本构关系、输送带经过辊子时橡胶与辊子的接触轮廓以及物料在输送带上的载荷分布等因素。各类研究主要在以下几个方面存在差异。

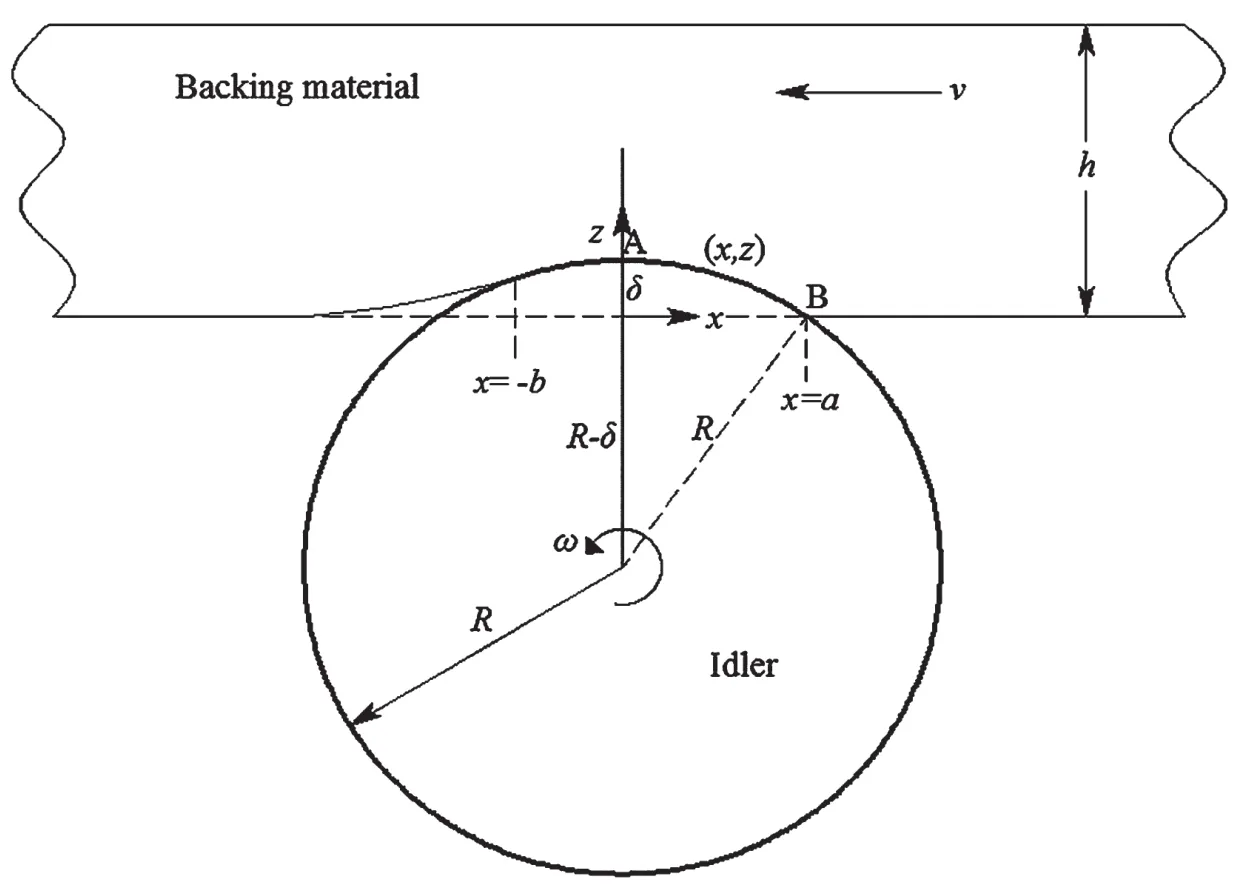
图1 输送带经过辊子的变形图

图2 输送带橡胶材料的主曲线图

（1）模型的维数。Spaans、Jonkers、Qiu以及Rudolphi和Reicks主要来自采用的Winkler基础假设。Winkler基础假设使粘弹问题通过假设一维压力状态并完全地忽略剪应力和材料的不可伸缩性，求解相对简单。Qiu、王繁生也采用二维模型进行求解，需要用复杂的边界元方法求解，Munzenberger采用三维有限元模型进行求解。

（2）覆盖橡胶的本构关系。作为粘弹性体的输送带覆盖层，可采用广义Maxwell模型来描述其本构关系，可采用3元件模型进行简化，见图3。

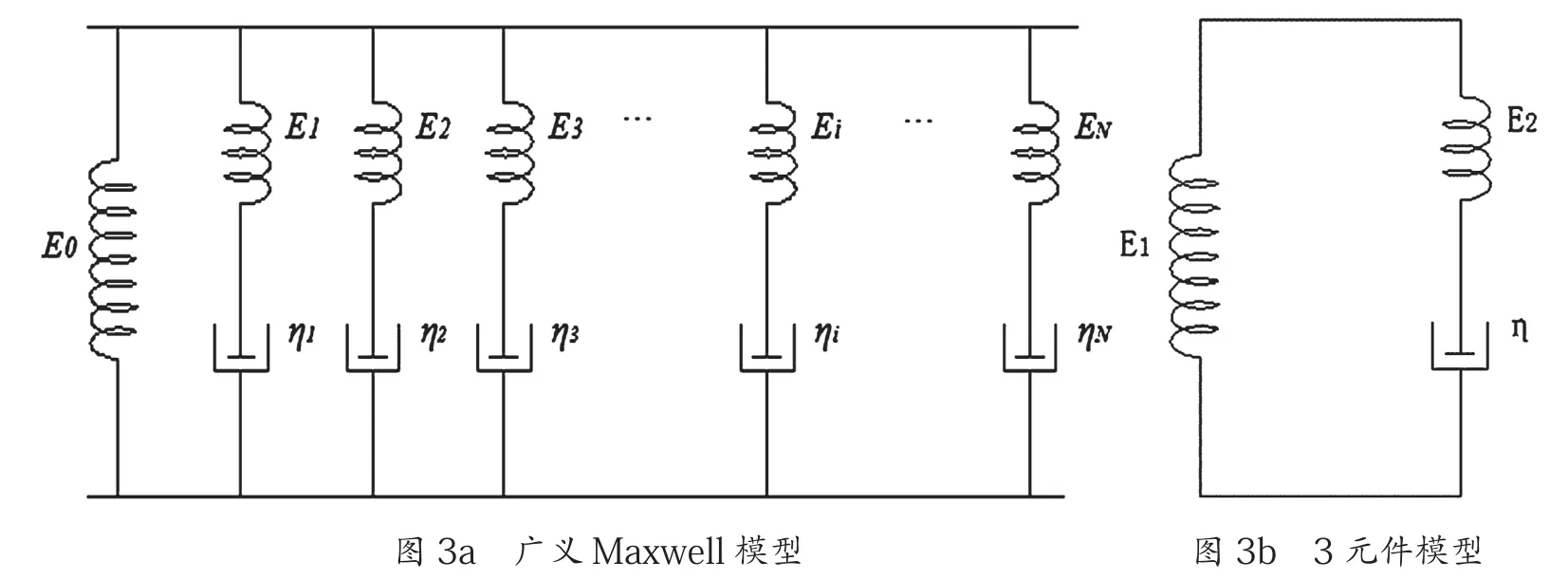
图3 输送带的本构关系图[41]

（3）环境温度与带速。具有流变特性的橡胶对温度和施加载荷的频率敏感，不同温度和频率条件下的弹性模量和损耗模量不同。

（4）相对于辊子压陷接触轮廓的对称与非对称。Jonkers采用对称假设可直接得到解析解，而采用非对称结构时需要通过解非线性方程得出非对称的接触区域长度。

2 压陷阻力的相关测试方法

压陷阻力的确定一般有小试样和大试样两种方法，两种方法的原理本质上是相同的，但由于存在模型的参数误差和测试误差，所以最终结果会存在一定差异。

2.1 小试样参数的测量与确定广义Maxwell模型参数

小试样方法是研究输送带覆盖层上取出3 mm×12 mm×30 mm的试样，使用扭转流变仪获得温度、应变和频率等所有范围的输送带覆盖层的动态物理性质E´（弹性储能模量）和E〞（耗散模量）。当给试样一定频率，可测得应力σ0与应变ε0的关系，应变曲线相对于应力曲线有滞后相位角δ，见图4。图5为RSA-G2流变仪及其试样的固定方式。

图4 粘弹性行为图

图5 RSA-G2固体分析[34]图

从而有：

进行时间-温度叠加数据是由样品的温度和频率扫描获得的。此测试包括：频率变化时保持温度和应变常数不变，然后将温度逐渐递增，并在一段时间的新的温度保持不变，以确保频率扫描再次执行之前整个材料的温度不变。图6为测得的流变参数-温度关系曲线。储能模量，损耗模量和的数据的主曲线（见图7）来源于时间-温度扫描，该扫描中温度和频率的关系用WLF（Williams，Landel and Ferry）方程[42-43]得出。

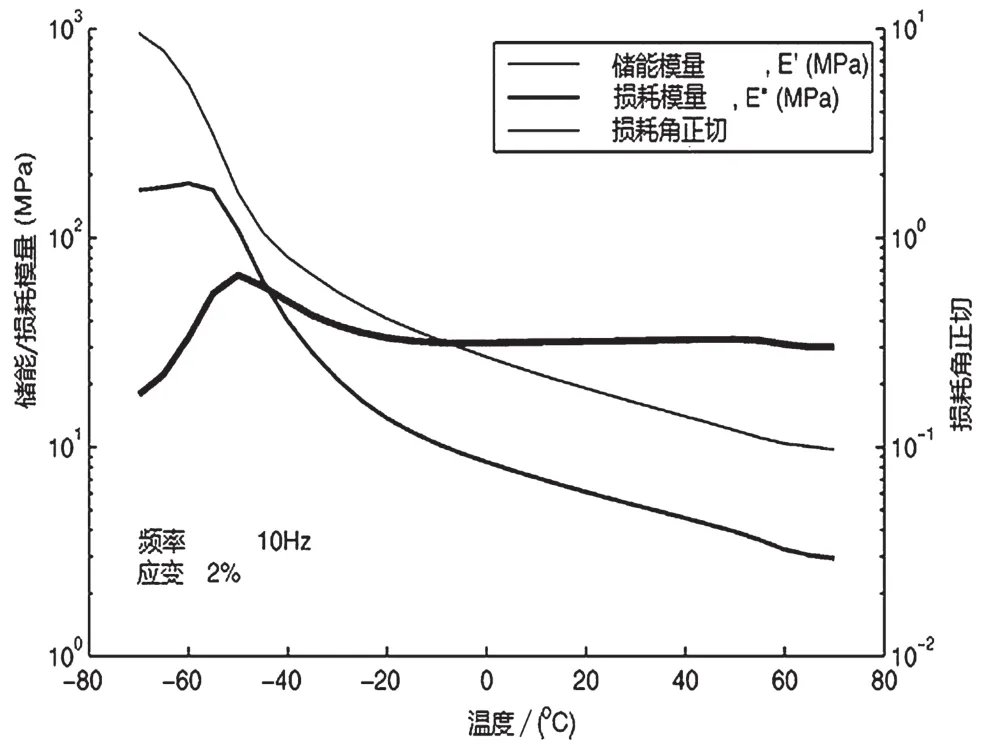
图6 流变参数-温度关系曲线图[34]

图7 从时间-温度叠加的主曲线图[34]

其中，C1、C2：常数，由经验数据确定；aT：位移因子；T0：参考温度；T：温度。

在WLF方程中，只有aT和T为独立参数，可以通过多项式拟合函数关系：

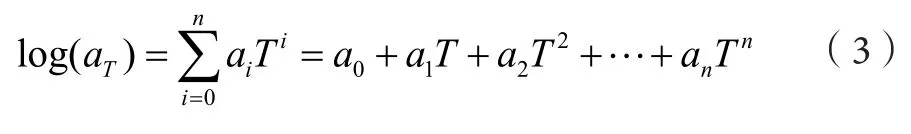
通过主曲线确定常数ai。此计算式在CEMA6中采用。CEMA7中直接采用式（2），并且考虑了带速对接触频率的影响。实际上也可以采用其他形式的函数进行插补拟合。

按照广义2N+1参数模型，可以通过Prony级数给出应力响应函数：

其中τi=ηi/Ei是机械模型中各个耗散元件的周期特征参数。

采用对主曲线的拟合来得到E0、Ei和τi。

来计算E0和Ei。

由于Ei和τi的数量级差别较大（主曲线的横、纵坐标都采用对数坐标），在应用式（5）求解Prony级数（Maxwell–Weichert）参数时所得代数方程组为病态方程，Rudolphi采用最小2乘法通过主曲线来得到Prony级数参数，存在较大的误差。

通常，通过扭转测量所得结果为剪切模量，材料的剪切模量和弹性模量的关系为[43]为泊松比，橡胶为μ=0.5。

2.2 大试样测试方法

大试样方法使用包括上覆盖层、骨架和下覆盖层等输送带所有部分构成的接头后无极输送带，尺寸为350 mm宽，4800 mm长（13.8×190 in）。压陷阻力是在不同托辊载荷、带速和温度下测得。DIN22123是大试样测试方法。采用大试样的结果可直接计算出压陷损耗。图8为压陷滚动阻力测试结果示例[19,40]。

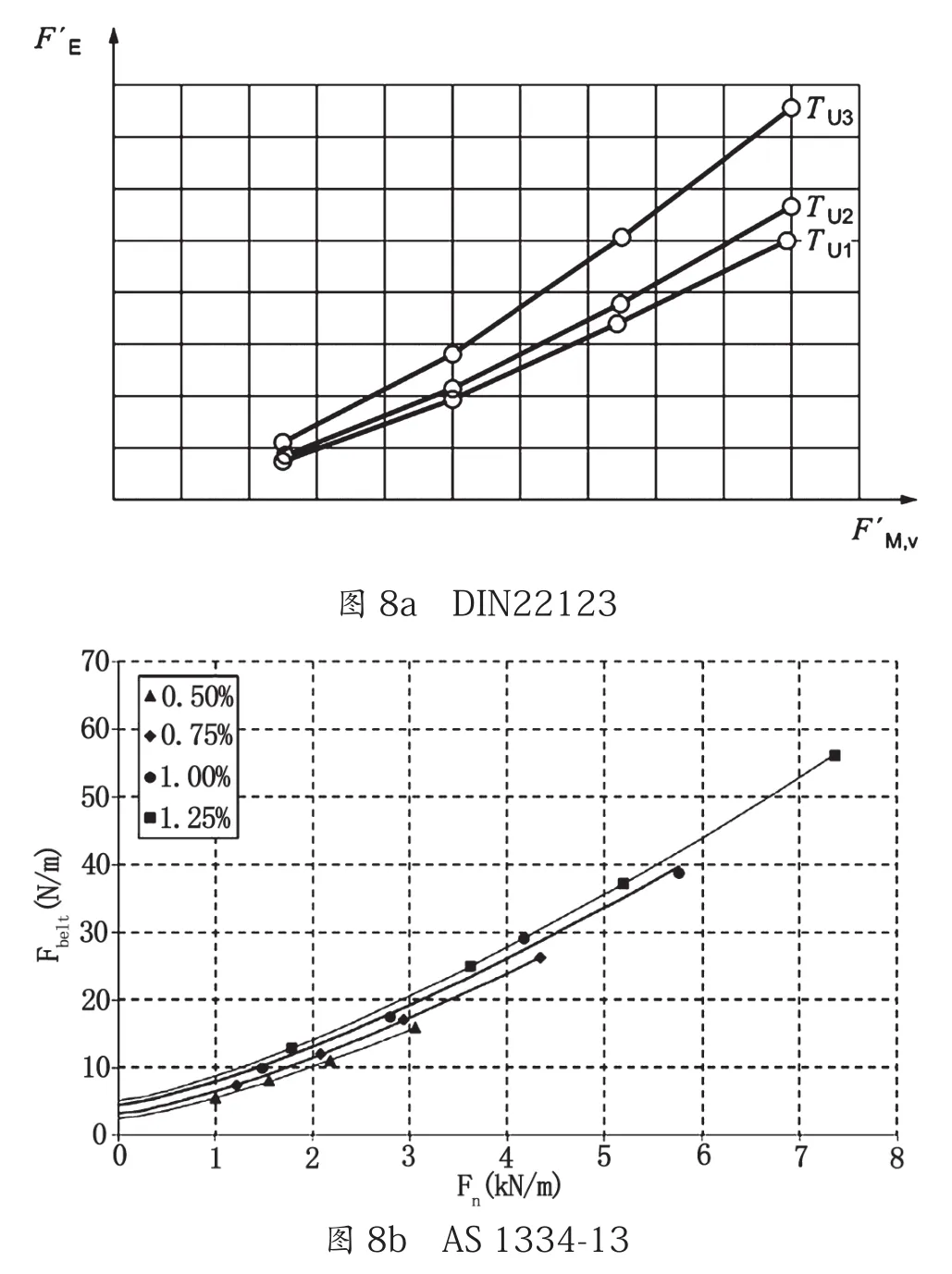
图8 压陷滚动阻力测试结果示例图

3 压陷阻力的计算方法

3.1 JONKERS压陷滚动阻力模型

常用滚动阻力模型是由Jonkers提出的。其计算式是用水平力推导的，滚动压陷阻力Fj为：

式中，W为输送带和物料产生的单位宽度垂直载荷，h为输送带下覆盖层厚度，D为托辊直径，材料特性E´和δ分别表示输送带底部的储能模量和损耗角。

Jonkers计算式从粘弹性简单的模型导出，滚动阻力计算结果偏高。Lodewijks、Wheeler、Rudolphi、Qiu详细讨论了Jonkers方程的局限性。Jonkers采用一维Winkler基础假设，假定负载和压陷深度之间存在线性关系，而通常对于大多数橡胶配料载荷或变形响应只有在非常小的应变时才是线性的。托辊建模为一个刚性圆柱体，输送带轮廓被假定为对称于托辊的中心线；然而，在典型的运行速度，压陷轮廓通常是不对称的。

以Jonkers模型为基础，现已开发使用了更为准确压陷模型。然而，因为它的能量损失和动态的材料特性，Jonkers方程仍然是最常用的模型，它说明滚动阻力与成正比例关系。

3.2 QC-N压陷滚动阻力模型

相对于简单的Jonkers模型，QC-N模型是发展成为一个在理论上更准确的描述压陷滚动阻力的新模型。类似Jonkers，主要弯曲橡胶数据可以直接应用到模型，不同于由Lodewijks、Rudolphi和Reicks开发的分析模型需要麦克斯韦-维切特（Maxwell–Weichert）参数来表示橡胶的粘弹性性质。和其他一维模型一样，Qiu-N模型假设输送带简化为在刚性托辊之上的Winkler基础。假设接触的轮廓被为半正弦函数曲线。模型包括一个“瞬态项”是考虑到压陷变形的接触应力瞬态响应，这是其他的一维模型所忽略的。

计算式是用水平力推导的，是滚动压陷阻力：

式中，W为由输送带和物料产生的单位宽度垂直载荷力，h为输送带下表面覆盖层厚度，R表示托辊半径，材料特性δ表示带底部的损耗角，由等式（8）确定，DQ是由等式（9）确定的无量纲值，A(α)是DQ的参数，由等式（10）确定。

G´和G〞分别为主曲线的剪切弹性模量和剪切损耗模量。

相位角α=ωt，ω表示频率，t表示时间。α*由等式（11）确定，表示压陷最大处到托辊皮带接触后沿与压陷最大处到托辊输送带接触前沿的比值。

虽然QC-N的模型并不如Jonkers方程能够简单地实现，但它表明能量损失和动态的材料特性之间有直接关系，其中滚动阻力正比于(1/3)。这可以用于橡胶胶料的快速比较。Qiu比较了几种不同计算方法见图9。

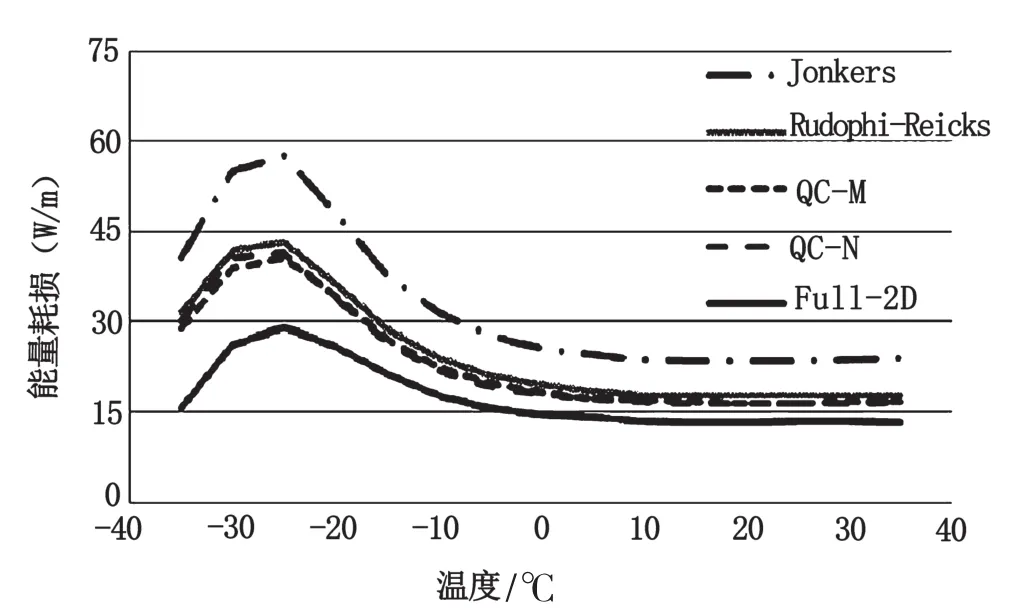
图9 几种计算方法能量损耗与温度函数关系曲线比较图[22]

QC-N模型避免了Prony级数参数的求解，但仍然是将输送带与托辊的接触看作是准对称结构，只是满足了非对称接触的边界条件。

3.3 Prony级数参数的求解方法

对Prony级数参数求解困难问题，可通过将式（5）转换为优化问题，再采用智能优化算法进行求解，从而避免了求解代数方程的病态问题。

首先，定义 x1=E0,x2=E1,x3=τ1,…,x2i=Ei，x2i+1=τi(i=1,2,…,N)，X=[x1,x2,x3…x2i,x2i+1]T，则方程组（5）可以转化为：

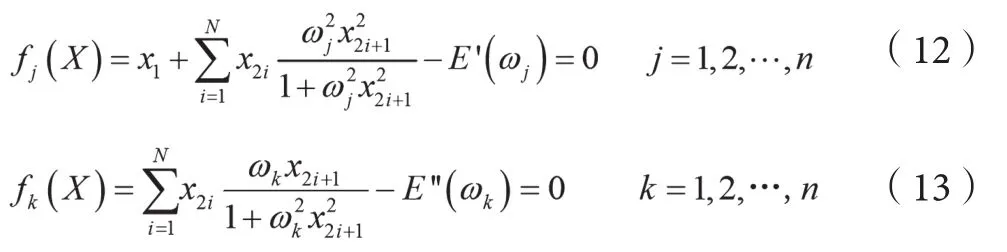
方程组（12）、（13）转化为最优化问题，即求解fi(X)、fk(X)最小值。

定义目标函数f(X)为：

即fi(X)、fk(X)相对误差的和。

则E0、Ei、τi的求解问题就可以转化为如下最优化问题：

此外，在计算的过程中还尝试了另外两种目标函数，即：fi(X)和fk(X)的平方和、fi(X)和fk(X)绝对值的和，但是效果都明显不如fi(X)和fk(X)相对误差的和。图10为将主曲线用13项和1项（3参数）Prony级数拟合的结果。可见，采用3参数模型与实际橡胶的储能（耗散）模量差异较大，其损耗角也会产生较大的误差。

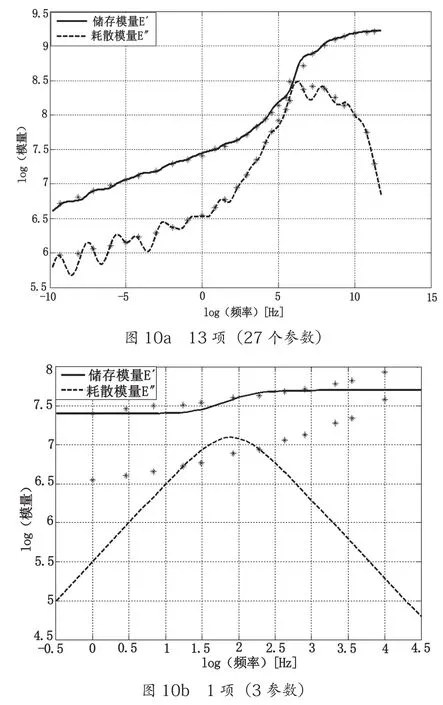
图10 主曲线的Prony级数的拟合图

4 其他主要阻力分量

Hager[14]对长度为1km的带式输送机进行各种阻力计算，见图11，其结果为压陷滚动阻力占总阻力的61%，托辊轴承阻力占6%，输送带弯曲阻力占5%，物料的内摩擦（物料弯曲）阻力18%，附加阻力占9%，其他阻力占1%。显然，这只有在特定条件下存在的，但大致反映了各部分阻力所占比例关系。

图11 1km长水平带式输送机各种阻力的比例关系图

4.1 物料内摩擦阻力

物料的内摩擦（弯曲阻力）是由于输送带经过托辊组时物料被抬起，之后是下降，同时伴有物料在横向的“张”、“合”运动。

Spaans[7]根据Krause和Hettler的作用在托辊组辊子上的主动和被动侧压系数，给出计算物料弯曲阻力为：

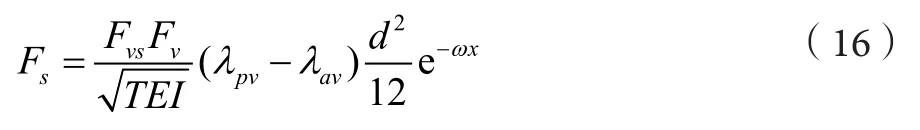
其中，Fvs为物料重力作用在托辊上的正压力；Fv为输送带和物料重力的垂直分力；为输送带张力；EI为输送带的弯曲刚度，Nm2；λρv——在垂直面上的主动侧压系数λa；λav为在垂直面上的被动侧压系数λp。

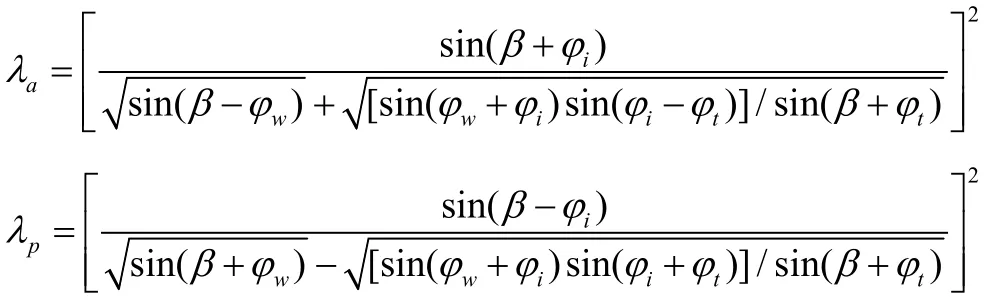
式中，β为槽角；φw为输送带与物料间的摩擦角；φt为物料堆积角；φi为物料内摩擦角；ω为；x为从托辊上刚性槽形过渡到松弛的距离，0.01＜x＜0.04；d为物料的厚度。

Wheeler[29，33]采用实验与有限元方法进行来确定压陷阻力，难以在工程中应用。

4.2 输送带的弯曲阻力

Spaans采用梁弯曲模型，给出输送带的弯曲阻力计算式为：

ψb——弯矩的迟滞损失∆M正比于所施加的力矩M。弯曲输送带的能量损失系数，ψb=∆M/M。其主要问题是确定弯曲输送带的能量损失系数较困难。Wheeler在压陷阻力实验台上通过施加输送带弯曲变形，根据实验结果推出输送带弯曲阻力[40]。

4.3 托辊的轴承阻力

Spaans给出托辊阻力的计算式为：

这里的n是托辊组中的托辊数，v是带速，D是托辊直径。

托辊轴承阻力可采用SKF的轴承阻力计算方法，但是该方法过于复杂[45]。Kruse和Lemmon[46]比较了Spaans、SKF、CEMA6的托辊阻力计算方法，在20℃的条件下，Spaans与SKF很好地吻合，而CEMA6的结果偏大；在-10℃的条件下，同样地CEMA6的结果偏大。

4.4 物料和输送带在托辊上的载荷分布

在计算压陷滚动阻力和物料弯曲阻力时，需要给出物料和输送带在托辊上的载荷分布。然而，确定载荷分布是困难的，它受到物料的种类、粒度分布、物料在输送带上的填充率以及托辊组的结构、输送带的横向刚度（成槽性）、张力等因素的影响，因此DIN22101的通过测试来确定主要阻力的方法也没引入物料弯曲阻力，只采用托辊旋转阻力和压陷滚动阻力来折算。Grimmer等[47-50]在研究平面转弯带式输送机的设计问题中给出了物料在各个辊子上的载荷分布比例关系。Ilic和Wheeler[37]采用DEM仿真和三维激光测量、以及Tekscan压力传感器测量输送带的轮廓和物料作用在输送带的压力。Liu等[51-52]采用相同的是检测装置进行测试，图12为所用传感器和现场测试情况。CEMA7中也给出了一种物料在输送带的载荷分布，但尚不能得到业界的认可。DIN22123和AS 1334-13均采用线性载荷分布，见图13。

图1 2所用传感器和现场测试情况图

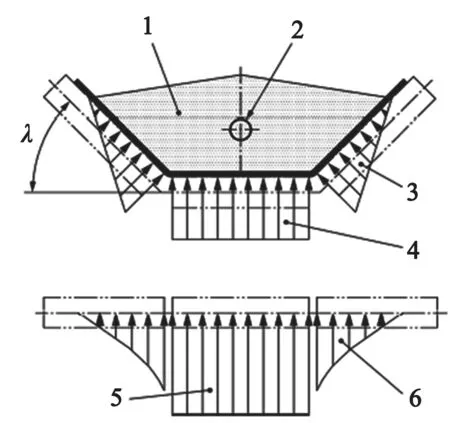
图1 3等长辊子的托辊组设置在水平直线区段上理想化的正压力分布图

5 特种阻力和附加阻力

带式输送机的特种阻力和附加阻力是除主要阻力和提升阻力外阻力，之所以单独划分出一类附加阻力是由于20世纪70年代前受到计算工具的限制所造成的。近年来相关研究较少，值得注意的是：ISO5048的输送物料与导料槽侧板间的摩擦阻力的计算式过于简化，该计算式已经在DIN22101-2002中进行了修改，且ISO5048的计算结果过大。表1为带式输送机的计算实例，从计算结果看，滚筒阻力在各项特种与附加阻力所占比例较大，建议在设计计算中不要忽略该阻力。曲线段阻力的凸、凹弧部分具有相互抵消作用，但凸弧段在高张力区，还会产生一定的曲线段阻力。

表1 各部分阻力所占比例的计算实例表

6 带式输送机阻力计算与设计的问题

Lodewijks[9]认为，存在的事实是：①通过应用橡胶粘弹性理论模型可以帮助预测带式输送机的能耗。②对橡胶的机械/动态特性测试应遵从科学的方法。③可以比较两种不同配方的橡胶的特性。此比较仅能基于测试特定流变仪的橡胶。测试的机械/动态特性可以作为压陷滚动阻力的输入参数，它能够用以比较压陷滚动阻力和/或系数。④可以通过特定的测试装置测试不同橡胶配方下的橡胶机械/动态特性，用以采用计算设计工具对带式输送机的功率需求进行估计。

然而，作为虚构：①应用特定的流变仪测试的橡胶机械/动态特性可以应用到任何的设计模型得出同样预测精度的系统能量消耗。②理论模型预测与现场实测的带式输送机系统的功率消耗误差在5%以下。③对于长距离越野带式输送机，压陷滚动阻力总是起主导地位的设计参数，一些情况下，例如下运的带式输送机系统高的压陷滚动阻力可能是有益的。另一些系统，例如大倾角输送机，橡胶的损耗在总功率损耗中相对较小，甚至可以忽略。④在带式输送机安装后应尽早测试功率消耗，以对理论计算和实际功耗进行比较。

在带式输送机安装后的半年，橡胶的性质将会发生快速的变化，在投入运行半年内测得的功率消耗不能表示系统将来的功率消耗。这种影响在进行橡胶配方的机械/动态测试时也应予以考虑，阻力计算中应注意以下内容。

（1）CEMA计算方法不是标准，但由于CEMA的影响力往往被认为是事实上的标准。然而，CEMA6和CEMA7的计算方法是一个商业上的计算方法，仅依据CEMA设计指南很难进行计算，且通常不能直接将计算结果作为最终设计，CEMA计算方法也不被美国的业内所完全接受[5，46]。

（2）带式输送机运行阻力在全生命周期中是不断变化的，从安装初期的跑合到寿命后期的零部件的老化（损坏），运行阻力也会从大到小，再变大。

（3）在设计过程中，对主要部件的运行阻力测试有助于带式输送机系统的设计；但由于测试的内容很难涵盖全部的运行工况，尚需要在设计过程中进行必要的修正，以保证系统安全可靠地运行。无论采用何种设计计算方法都依赖于设计者的最终判断。

（4）低滚动阻力输送带的使用需要特别注意其适应的温度范围，有的低滚动阻力输送带在合适的温度范围下具有较低的压陷滚动阻力，而在其他温度下可能阻力更大。

（5）采用小试样和大式样测试与计算所得压陷滚动阻力会有很大的差别，因为两者所存在的误差来源有很大不同。