风力机塔架在风—近场强烈地震耦合作用下的倒塌分析*

2018-08-20高庆水邓小文张楚田丰刘石

特种结构 2018年4期

高庆水邓小文张楚田丰刘石

（广东电网有限责任公司电力科学研究院广州510080）

引言

随着风能工业的发展，越来越多的风场建在地震活动区，值得注意的是，一些风能丰富的地区存在高地震烈度的风险，如中国的东南沿海就处于该区域内。在这些地区的风场还可能处于潜在的地震断裂带上，存在遭受近断层速度脉冲型地震作用的风险。近断层脉冲型地震动具有类似脉冲的波形、较大的速度峰值和脉冲周期以及丰富的中长周期分量，研究表明［1］在这类地震动作用下中长周期结构将产生很大的破坏。风力机塔架结构的质量主要集中在塔顶，具有较长的自振周期，是典型的高耸结构，目前已有学者对近断层地震动作用下风力机塔架的动态响应进行了研究，如Stamatopoulos［2］研究了位于希腊地震区断裂带附近风力机的地震响应特征，研究表明利用时程分析方法计算的基底剪力和倾覆弯矩比按弹性反应谱分析的结果要大，因此，希腊抗震规范中关于近场区的弹性加速度反应谱需进一步改善；Sadouski［3］等研究了近场和远场地震动作用下筒体具有初始缺陷的风力机塔架动态响应特征，在近场脉冲型地震动作用下塔架的损伤比远场地震动作用下严重很多；弓卫［4］选择台湾集集近断层地震动记录作为地震动输入，将其分为无速度脉冲和含速度脉冲两组，利用ANSYS有限元软件对风机塔筒结构进行了地震时程分析，求得风机塔筒结构的顶点位移、顶点加速度、底部剪力和底部弯矩，对比分析发现含速度脉冲型地震动作用下风机塔筒结构的地震响应要大得多；为减小近断层地震动作用下风力机塔架的动态响应，陈俊岭等［5］提出采用滚球减振器的措施减小塔架结构的地震响应；虽然对近断层地震动作用下风力机塔架的动态响应研究取得了一些成果，但Katsanos等［6］在其最近的综述文章中提到近场地震动对风力机塔架的影响仍需作进一步研究。

近年来一些学者开始研究风和地震耦合作用对风力机塔架的动态响应的影响，如Asareh等［7-9］利用ABAQUS有限元软件研究了风和地震耦合作用下5MW风力机塔架的地震易损性，并考虑了平均风速大小的影响，结果表明风荷载对风力机塔架地震易损性影响不大；曹必锋等［10］推导了风力机塔架在风和地震耦合作用下的动力学运动方程，通过对某3.0MW风力机塔架动力响应进行计算，获得了风力机塔架在风和地震耦合作用下的塔架顶部位移和底部剪力，计算结果表明在风和地震耦合作用下的塔架顶部位移较风荷载独立作用下大47.2%；杨阳等［11，12］基于FAST开源软件和Wolf土-构耦合模型建立了风力机地震工况动力学仿真模型，并计算了5种不同平均风速的气动载荷与101种不同强度的地震载荷联合作用下风力机的动力学响应，结果表明在额定风速下，气动载荷与地震载荷之间为非线性耦合，评估风力机地震动力学响应时，必须充分考虑风和震耦合效应。

通过以上文献综述可知，虽然一些学者在近断层地震单独作用以及风和普通地震耦合作用下风力机塔架的动态响应进行了分析，但在风和近断层脉冲型地震耦合作用下的研究鲜有报道，而且对强烈地震动作用下风力机塔架的倒塌特性的研究也较少。本文基于ABAQUS有限元平台，利用非线性组合随动强化模型模拟塔架钢筒体的本构关系，计算了在风和近场脉冲型地震动耦合作用下风力机塔架的动力响应，研究了脉冲周期对塔架地震响应的影响，最后研究了风力机塔架在强烈近场地震作用下的抗倒塌能力和倒塌特性。

1 有限元模型的建立

1.1 单元的选择

建立风力机塔架的有限元建模时，为减少建立模型的工作量，在不影响风力机塔架结构本身动力特性的前提下，可以忽略对其影响很小的一些附属构件，对复杂部位进行适当的简化。风力机塔架通常是薄壁圆筒壳体，根据其几何特征和受力特点可将其简化成壳单元来处理。机舱和轮毂的重量作为集中点质量加载在塔架顶端，忽略其形状对结构的影响。叶片为变截面的细长杆件，故可将叶片简化成分段弹性梁单元来处理。考虑到叶片和塔架之间的相互作用，用一个刚度很大的梁单元将叶片和塔架连接起来。机舱和轮毂用集中质量单元模拟，分别置于塔架的顶部和叶片的连接中心。风电塔架的底部一般是用螺栓与地基连接，为了建模简便，直接将底部固定，即约束所有自由度。风力机塔架的有限元模型如图1所示。

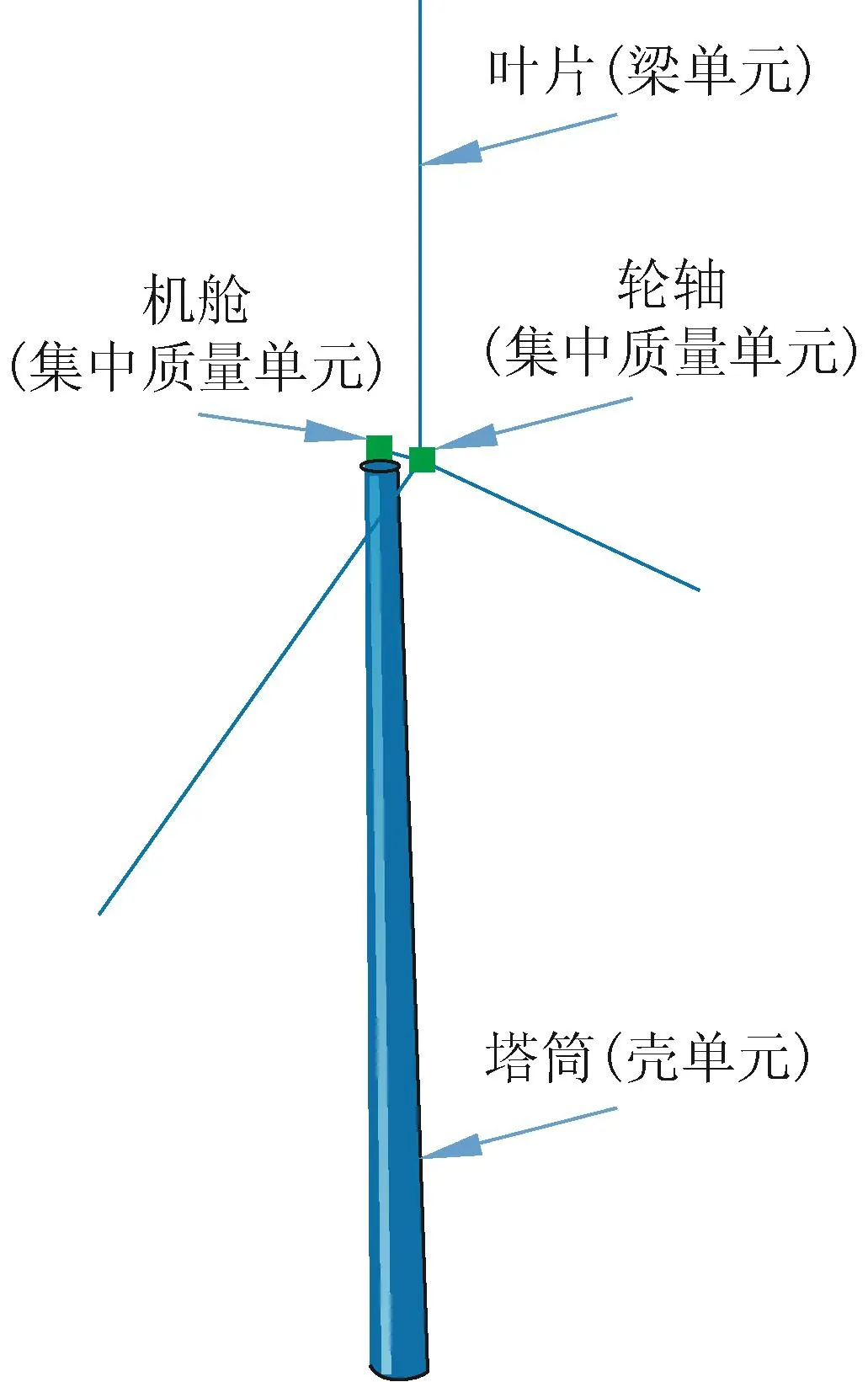
图1 风力机塔架的有限元模型Fig.1 Finite element model of wind turbine tower

1.2 材料的本构关系

本文采用非线性组合随动强化模型模拟钢塔架筒体的本构关系［13］，该模型的加载面既有均匀膨胀又有平移，可以有效地模拟材料加载过程中的强化效应和包辛格效应，该模型的等效屈服面定义为：

式中：σ为应力张量；S为偏应力张量；αdev为偏背应力张量；σ0为强化屈服应力。

1.3 有限元模型的验证

2010年加州大学曾经选择一座高21.9m的小型风力机塔筒对其进行了静力试验，塔筒由5部分组成，其具体尺寸见文献［14］。塔架的材料为钢材，弹性模量为210GPa，泊松比为0.3，屈服强度为270MPa。试验时将塔底固定，在塔顶逐步施加位移荷载使塔架发生变形，测得塔底的剪力和塔顶位移的曲线见图2a。

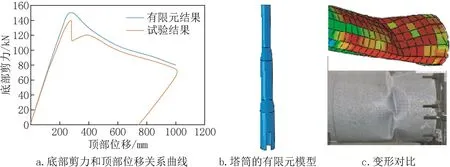
图2 有限元模型的验证Fig.2 Finite element model verification

为验证有限元建模方法的正确性，采用ABAQUS对该塔筒进行了有限元建模（见图2b），将模型底部固定，在塔顶施加位移，提取出塔底剪力，画出底部剪力和顶部位移的关系曲线（见图2a）。由图2a可知，当塔顶位移较小时，塔底剪力随塔顶位移线性变化，当位移增大到0.2m时，塔架中部开始出现屈服状态，当位移达到0.3m时，底部剪力达到最大值155kN，此后随着位移继续增大，底部剪力反而减小。图2c还给出了塔筒破坏时的局部变形对比，从图可知，ABAQUS有限元建模的计算结果与试验结果基本一致，验证了有限元建模方法的正确性。

2 风荷载的形成和地震波的选择

2.1 风荷载的形成

当风通过风力机时将产生升力和阻力，升力使叶片产生旋转，阻力使叶片和塔架顺风向前后振动，本文只考虑阻力的影响，任何时刻作用在塔架和叶片上的风荷载计算公式为［15］：

其中：Cd为阻力系数；ρ为空气密度；V（x，y，z，t）为瞬态风速；A为作用面积。

结构上任意一点的瞬态风速V（x，y，z，t）等于平均风速与脉动风速和，即：

式中：v10为标准高度（10m）处的平均风速；z为计算点离地面的高度；α为地面的粗糙度指数。

脉动风速部分可以用零均值的高斯平稳随机过程来模拟，它的产生需要用到理论的或者测量的功率谱密度函数，本文采用EN61400-1［17］中提供的Kaimal谱，其公式如下：

式中：S（f）为脉动风速的单边功率谱；f为频率（Hz）；Lk为风速的尺度参数；σ是风速的标准差；Vhub为轮毂处的平均风速。

风场具有空间相干性，主要表现在空间中各点风向和风速的不同步，当某一点的风速值达到最大值时，距离该点越远的点，其风速值达到该值的可能性就越小。脉动风在空间上的相关性主要包括左右、上下及前后相关。由此可知，对于风力机塔架而言，任意两点i和j的脉动风速空间相关系数表示为如下形式［18］：

式中：r为空间两点i和j的空间距离；Lc为长度尺度参数。

由式（5）、式（6）可得到风力机塔架上任意两点i和j的互功率谱密度函数为：

如果要模拟出n条风速时程，就要产生n个平均值为零的平稳高斯随机过程vi（t）（i=1，2，…，n），其互谱密度矩阵如下：

对S（f）采用Cholesky分解，得到下三角矩阵，H（f）第i点的模拟风速时程可根据式（9）获得［18］：

2.2 地震波的选择

近年来随着风电规模的急剧增长，风力发电机组也可能分布在近断层的地震带上，风力机塔架存在承受近断层地震动作用的风险。近断层地震动最显著的特点是方向性效应和滑冲效应引起的脉冲型地面运动，并以速度脉冲型地面运动最为常见。这种速度脉冲型地震动具有类似脉冲的波形、较长的脉冲周期和丰富的中长周期分量，地面速度峰值（PGV）与地面加速度峰值（PGA）的比值较大，通常PGV/PGA≥0.2。风力发电机塔架是长周期结构，在近断层的地震动作用下将产生很大的地震响应，甚至发生倒塌破坏。

本文根据以下原则选择近断层地震波：为保证所选地震波具有脉冲特征，要求地震波的PGA＞100gal、PGV＞30cm/s、脉冲指数PI＞0.9［19］、矩震级＞5.5，为研究脉冲周期对结构地震响应的影响，所选近断层地震动的脉冲周期在1.4s～12.2s之间。共选择了20条符合以上条件的近断层地震波（见附表1，所选的地震波来自文献［19］）。为了进行对比研究，还选择了20条普通远场地震波作为输入（见附表2，所选的地震波来自文献［20］），所选远场地震波的断层距＞50km、矩震级≥5.5。

表1 钢塔架材料各参数的取值Tab.1 Material parameters of the steel tower

3 算例分析

3.1 模型介绍

本文研究的风力机轮毂高60m，塔架是一个锥筒形的薄壳，外部直径由底部的3.8m线性递减到顶部的2.3m，壳在整个高度上的厚度都是35mm。钢塔架各参数材料的取值如表1所示。叶片横截面是空心矩形截面，叶片横截面高度是2m，宽度是0.8m，长度是30m，叶片厚度是15mm。叶片的弹性模量是65GPa，泊松比是0.2，密度是2100kg/m3。机舱的质量为50000kg，轮毂的质量为20000kg，塔架和叶片的偏离距离为5m。

用ABAQUS软件对该风力发电塔架进行有限元建模，采用薄壳单元S4模拟筒形塔架，叶片采用弹性的Beam31单元模拟；考虑到叶片和塔架之间的相互作用，用一个刚度很大的梁单元将叶片和塔架连接起来。机舱和轮毂用集中质量单元模拟，分别置于塔架的顶部和叶片的连接中心，结构的有限元模型如图1所示。

3.2 静态Pushover分析

对塔架进行Pushover分析可以观察结构的非线性行为，并据此定义塔架结构的破坏性能水平。本文采用位移控制的方法在塔架顶部沿前后方向逐步增加位移，得到底部剪力与顶部位移的变化关系曲线（如图3所示，图中还给出了塔架破坏时筒体的整体和局部变形图）。

图3 塔架的静态Pushover曲线Fig.3 Tower static Pushover curve

从图3可知，当顶部位移较小时，底部剪力与顶部位移呈线性变化，塔架还处于弹性阶段，当顶部位移达到2m时，塔架底部开始出现屈服现象，当位移达到3.8m时，底部剪力达到最大值3050kN，此后随着塔顶位移的增大，底部剪力反而减小。从塔架破坏时的变形可以看出，该塔架的破坏位置不在塔底，而在离塔底5m左右的位置。

3.3 风和地震耦合作用下的动态响应分析

利用ABAQUS的频率分析功能计算了塔架的固有频率如表2所示，本文计算的一阶频率与文献［18］中计算的一阶频率（0.57Hz）相近。

表2 塔架的振型和固有频率Tab.2 Vibration mode and natural frequency of the tower

该塔架位于某沿海风电场，通过查阅该地区的风速观察资料可知，风电场代表年［21］10m高度处的平均风速为5.12m/s，50年一遇最大平均风速为23.48m/s，各测点高度的平均湍流强度约为0.173～0.128。利用3.1节的方法模拟出风电机上不同位置的随机风速样本，其中风力机叶片上共30个点，塔架上共8个点（如图4所示）。图5分别给出了轮毂中心处（高度60m）和高度7.5m处的塔架上的瞬时风速时程。

图4 集中风载作用点Fig.4 The point of concentrated wind load

图5 瞬时风速时程Fig.5 Time history of instantaneous wind speed

通过场地的地震危险性分析，该塔架位于地震设防烈度8度区，多遇地震（50%，50年）对应的加速度峰值为0.11g，罕遇地震（2%，50年）对应的加速度峰值为0.51g。

首先计算只有风荷载作用下塔架的动态响应，由于地震时风力机通常处于停机状态，利用式（6）计算风荷载时程并导入ABAQUS模型中，利用瞬态动力分析模块可以完成风电塔架在停机状态下的风振响应计算。动力分析时塔架的阻尼矩阵采用瑞利阻尼，阻尼比取为0.5%，通过计算其中质量阻尼系数为0.213，刚度阻尼系数为0.004823。图6分别为代表年平均风速和50年一遇最大风速作用下塔架顶部的位移时程曲线。由图可知，两种工况下塔架顶部位移的最大值分别为0.028m和0.39m，远远小于Pushover分析中塔架开始屈服时的位移2m。由于代表年平均风速下塔架的瞬态风振响应很小，在以下进行塔架的地震-风耦合作用下动态响应分析时，平均风速将取50年一遇最大平均风速。

图6 风荷载作用下塔架顶部的位移时程曲线Fig.6 Time history curve of displacement curve of tower top under wind load

为研究纯地震作用的影响，把附表1中第10条近场波（时长为90s）和附表2中第14条远场波（时长为20s）的PGA调为0.51g，并沿风力机塔架的前后水平方向进行输入，计算了塔架顶端的位移时程（见图7），从图可知，近场波作用下的塔架顶端的最大位移为1.14m，远场波作用下的塔架顶端的最大位移为0.44m。

图7 地震作用下塔架顶端的位移时程曲线Fig.7 Time history curve of displacement of the tower top under earthquake

把附表1中第10条近场波和附表2中第14条远场波的PGA调为0.51g，并与风荷载进行联合作用，在风荷载作用60s后沿风力机塔架的前后水平方向分别输入这两条地震波，图8中给出了塔架顶端的位移时程曲线，60s以前由于只有风荷载作用，因此结构响应较小，60s后由于地震和风的同时作用，结构的响应突然增大，近场波作用下的塔架顶端的最大位移达1.45m，远场波作用下的塔架顶端的最大位移达0.86m。

为比较大量远场和近场地震波作用下塔架平均地震响应的大小，把附表1、附表2中所有近场和远场地震波的PGA调为0.51g，并与风荷载进行联合作用，图9给出了在20条近场地震波和20条远场地震波作用下塔架沿塔高的最大变形曲线。从图可知，当地震为近场脉冲型地震时，塔架的最大位移普遍比远场地震作用时大，远场地震作用下塔架顶端最大位移平均值为0.7m，近场脉冲型地震作用时塔架顶端的最大位移平均值为0.95m，比远场地震作用下大33.3%，但均小于Pushover分析中塔架开始屈服时的位移2m。为研究近场脉冲周期的大小对塔架地震响应的影响，图10给出了塔架顶端最大位移随近场脉冲周期的变化，但从图中可知，塔架顶端最大位移的大小与近场脉冲周期的大小相关性不大。

图8 风和地震耦合作用下塔架顶端的位移时程曲线Fig.8 Displacement time history curve of the top of tower under the coupling of wind and earthquakes

图9 塔架沿塔高的最大变形曲线Fig.9 The maximum curve of tower deformation along the height

图10 塔顶最大位移随近场脉冲周期的变化Fig.10 The maximum displacement of the tower with the near-field pulse period changes

3.4 风和地震耦合作用下的倒塌分析

在基于性能的结构抗震评价中，结构地震倒塌易损性分析的定义是在给定强度地震作用下结构发生倒塌的条件概率，其数学表达式为［22］：

式中：FR（·）为结构倒塌地震易损性函数；P（·）为结构倒塌概率；IM为地震动强度参数，本文取地面峰值加速度PGA作为IM。

设结构倒塌时的PGA值服从对数正态分布，则在给定PGA下结构发生倒塌的概率可按［22］：

式中：PGAi为第i条地震波作用下结构倒塌时的PGA。

以附表1和附表2中所有的地震波作为输入，并考虑风和地震的耦合作用，逐步增加各条地震波的PGA直到风力机塔架倒塌（即塔顶位移达到3.8m），风力机塔架倒塌时各条地震波的PGA如图11所示，利用图11的数据可以计算lnPGA|Collape和lnPGA|Collape，将其代入式（11）就可获得在远场和近场地震波作用下塔架倒塌破坏的地震易损性曲线（图12）。从图可知，塔架在罕遇的远场和近场地震（PGA=5.1m/s2）作用下倒塌的概率均很小，当倒塌概率为0.5时，近场地震对应的PGA为20m/s2，远场地震对应的PGA为27m/s2，说明该塔架具有良好的抗地震倒塌能力。