结合K-均值聚类分析的线性回归法在相关性分析中的应用
——以高考英语成绩与高考总成绩的相关性为例
2018-08-17董世荣
董世荣
(闽南师范大学外国语言学院,福建漳州 363000)
回归分析(Regression Analysis)是研究因变量y和自变量x之间数量变化规律,并通过一定的数学表达式来描述这种关系,进而确定一个或几个自变量的变化对因变量的影响程度。可以简单地理解为用一种确定的函数关系近似代替比较复杂的相关关系,用线性回归方程来描述其关系,进而确定一个或几个变量的变化对另一个变量的影响程度。回归分析所研究的主要问题就是如何利用变量x,y的观察值(样本),对回归函数进行统计推断,包括对它进行估计及检验与其有关的假设等,从而为预测提供科学依据。
目前,在外语定量研究中基本都是采用线性回归方法对两个变量间相关性进行研究。简单线性回归的原理是基于最小二乘法原则(即保证各实测点至直线的纵向距离的平方和最小)得到回归系数R2和回归直线在Y轴上的截距b[1-4]。本文把SPSS 19.0系统软件中K-均值聚类分析原理与一元线性回归原理相结合,提出一种研究两个变量间相关性的新方法。
1 数据与方法
1.1 数据来源
某校2014级某专业的学生,共计92人,以其高考总成绩与高考英语成绩为研究对象。
1.2 研究方法
(1)以样本的高考总成绩为因变量、高考英语成绩为自变量,对样本数据进行一元线性回归的相关性研究(以下简称方法一)。线性回归方法在SPSS 19.0统计软件中的设置方法如下:“Analyze”→“Regression”→“Linear”,从而得到相应的输出结果。
(2)结合K-均值聚类分析、再进行一元线性回归的相关性研究方法(以下简称方法二):设置聚类数,把高考总成绩变量作为被聚对象进行分类并迭代,把若干个最终聚类成绩结果作为Y轴数据。再对每个聚类数内的若干个高考英语成绩变量取平均值,并将这些均值数据作为X轴数据;然后对这两列数据(X轴和Y轴)进行一元线性回归处理,从而得到相应的线性方程和线性系数R2。
2 方法一的结果分析
2.1 数据来源的描述性统计
将92名学生的高考总成绩和高考英语成绩进行初步的统计分析,提取各项相关数据制表进行对比,其结果如表1所示。

表1 两种成绩的描述性分析
由表1数据显示,高考英语成绩和高考总成绩的标准差分别为13.41和8.746,说明该专业学生的整体水平差异比英语水平差异相对较小,同时也说明这些学生的英语水平参差不齐,差距较悬殊。另外,高考英语成绩与高考总成绩Pearson相关性的双侧显著性检验结果p为0.009,小于0.05,应否定零假设,即高考英语成绩与高考总成绩间不是独立的,存在着相关性,Pearson相关系数为0.269。
2.2 方法一在SPSS 19.0软件中的操作方法及计算结果
在主菜单栏中按“Analyze”→“Regression”→“Linear”和“Analyze”→“Graphs”→“Scatter”的顺序逐一点击鼠标,并进行相关设置;对92名学生的高考总成绩和高考英语成绩进行统计处理,提取出各项相关数据,并以高考总成绩为因变量y,以高考英语成绩为自变量x,其线性回归方程为y=0.173x+491.3。
该线性回归方程表明:高考英语成绩每增加1分,其高考总成绩约增加0.173分[4]。该方程中高考总成绩与高考英语成绩这两个变量间的相关系数R2为0.072,表明这两个成绩变量并不服从正态分布。
3 方法二的结果分析
3.1 聚类分析的原理
聚类分析又称群分析,是根据事物本身的特性研究个体分类的方法。通俗地说,就是指相似元素的集合,因此这种方法也常被称为逐步聚类分析,即先把被聚对象进行初始分类,然后逐步调整,得到最终分类。
SPSS软件中的聚类分析的原理如下:(1)根据用户提供的待分析数据的分布情况,结合用户分析需要所设定的聚类数目,采用距离最近原则进行分类;(2)逐一计算每一数据到各个中心点的距离,最后把各个数据按照距离最近的原则归入各个类别,并计算新形成类别的中心点;(3)再按照新的中心位置,重新计算每一数据距离新的类别中心点的距离,并重新进行迭代收敛,直到达到一定的收敛标准并形成最终的聚类中心。
3.2 方法二在SPSS 19.0软件中的操作步骤及计算结果
(1)在SPSS 19.0主菜单中按“Analyze”→“Classify”→“K-Means Cluster”的顺序逐一单击鼠标键,打开快速聚类主对话框。然后分别把高考总成绩变量移入“Variables”中,把高考英语成绩变量移入“Label Cases by”中。在“Number of Clusters”中,根据分析设置需要,填入相应的聚类分类数。其他的采用系统默认设置。
(2)在主对话框中分别打开“Save New Variables”和“Option”对话框,然后勾选“Cluser membership”及“Initial cluster centers,Cluster information for each case”选项,其他的按照默认设置即可。
(3)提取SPSS输出结果中Final Cluster Centers的高考总成绩数据于新建的Excel文件中,并作为Y轴数据;提取SPSS输出结果的Report中Mean数据(高考英语成绩),作为X轴数据;然后再将X轴与Y轴数据进行拟合直线作图,从而得到线性方程和线性系数R2。
(4)改变步骤(1)中Number of Clusters的数值,进行类似操作,得到不同聚类数时高考总成绩和高考英语成绩间的线性方程和线性系数R2(表2),并将聚类数m与线性系数R2进行作图(图1)。

表2 不同聚类数与线性方程及线性系数之间的变化关系
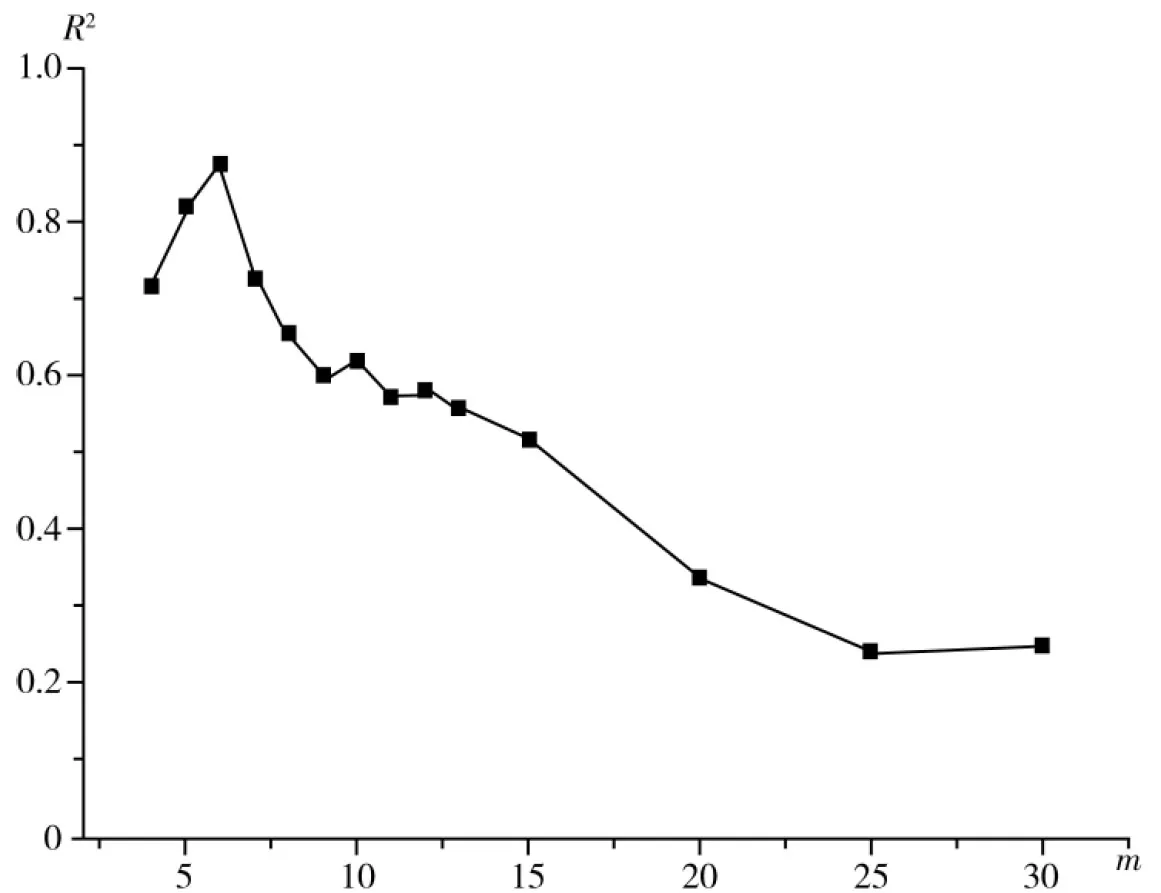
由表2数据显示,随着聚类数的不断增多,其相关系数的值也逐渐增大。当聚类数为6时,线性系数为0.875。然后随着聚类数增大,其线性系数又逐渐降低。但聚类数并不能无限增大,当聚类数超过高考总成绩的数量时,无法得到线性系数,例如这92位同学的高考总成绩分别为35个不同数值,则聚类数不能超过35,否则该方法无法使用。
4 两种方法在两变量相关性分析时的优缺点对比

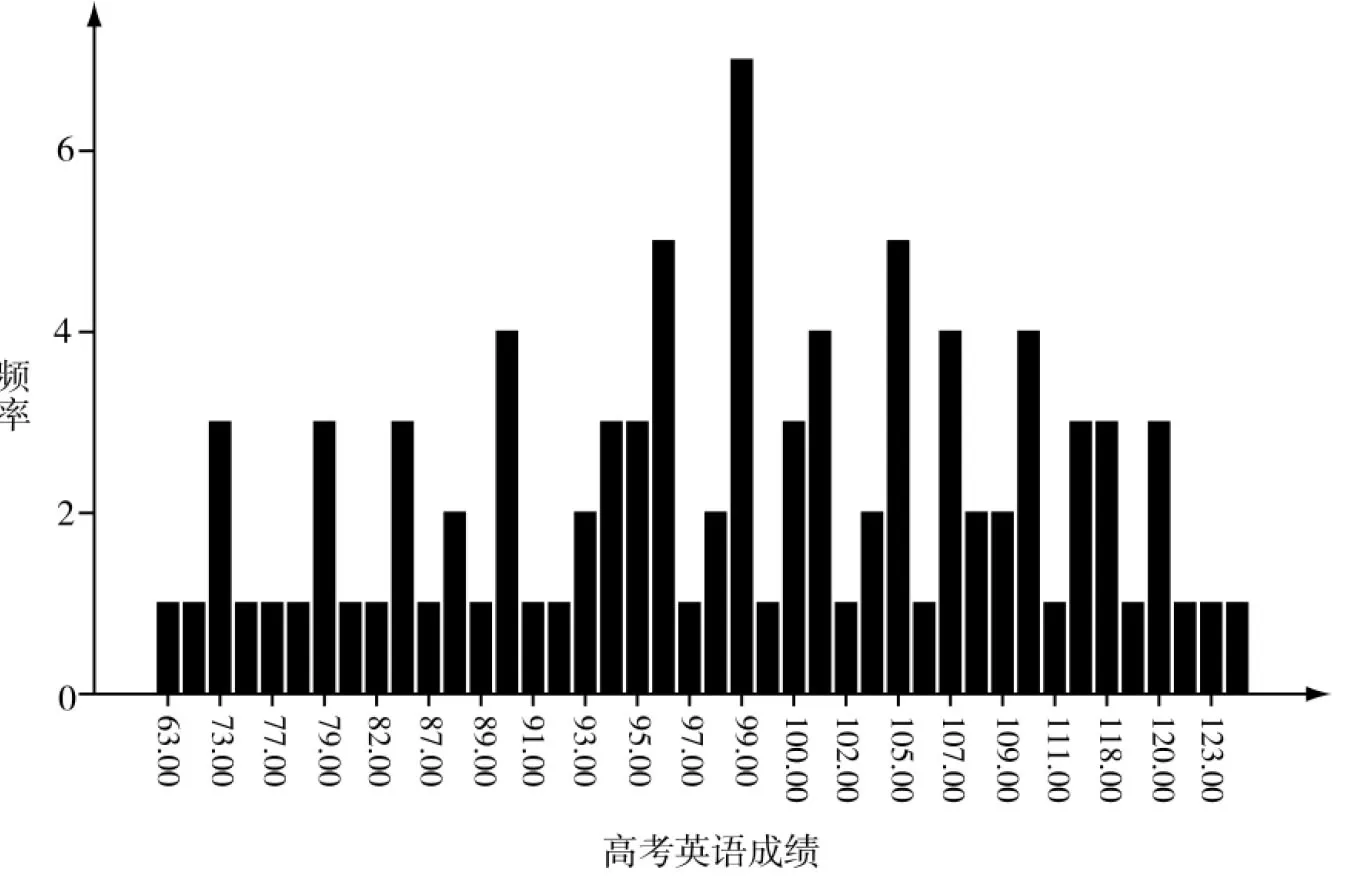
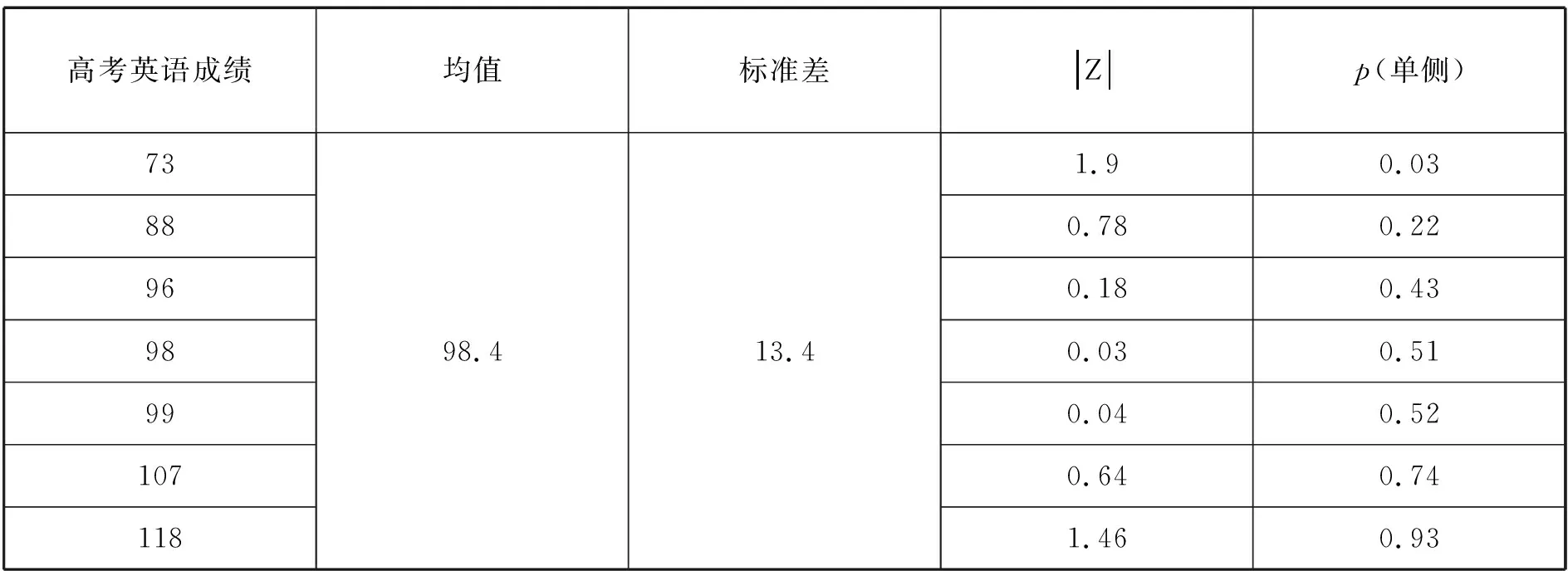
表3 高考英语成绩的正态分布分析

表4 两种方法在进行两变量间相关性分析时的差异对比
注:*实际高考总成绩:某一指定的高考英语成绩对应的若干个实际的高考总绩。可能的高考总成绩(1):指定某一英语成绩,采用方法一得到的高考总成绩。可能的高考总成绩(2):指定某一英语成绩,采用方法二得到的高考总成绩(6次和30次分别为聚类数,进一步对比不同聚类数在相关性分析中的差异性)。

对图3的研究结果表明:(1)以实际的高考总成绩的标准差为对照线(a线),当采用方法一(b线)进行相关性研究时,其在大于52%区域(图3中CD段区域)和小于3%区域(图3中AB段区域),离a线较近,表明采用线性回归(方法一)得到的高考总成绩与实际高考总成绩的偏差较小,即该方法在两变量间相关性分析时能够得到较合理的分析结果。(2)以实际的高考总成绩的标准差为对照线(a线),当采用方法二(c线和d线)进行相关性研究时,其在正态分布的3%~52%区域(图3中BC和CD段区域),c线与a线的距离及d线与a线的距离均小于b线与a线的距离。这表明采用结合聚类分析的线性回归法(方法二)得到的高考总成绩与实际高考总成绩的偏差较小,即该方法在两变量间相关性分析时能够得到较合理的分析结果。同时,不同的聚类数会对相关性分析结果造成一定影响。
5 总结
本文将某校2014级某专业学生的高考总成绩及高考英语成绩作为研究对象,分析了学生高考英语成绩及高考总成绩的相关性。研究结果表明,该专业学生的高考总成绩差异幅度比英语成绩差异幅度要小,英语水平总体参差不齐,差距较悬殊。
分别采用方法一和方法二对学生的高考英语成绩及高考总成绩的相关性进行分析。在高考英语成绩的不同分布阶段,两个方法各自有优缺点。因此,为了达到较高的合理性或准确性,当样本数据分布比较接近正态分布时,应采用一元线性回归法(方法一)进行两变量间相关性分析;当样本数据分布比较偏离正态分布时,应采用结合聚类分析的一元线性回归法(方法二)进行两变量间相关性分析。
