MHCSSA：一种基于多群分层协作策略的社会蜘蛛算法

张德成，王明星，王 杨，赵传信

(1.蚌埠医学院公共基础学院，安徽蚌埠 233000；2.安徽师范大学计算机与信息学学院，安徽芜湖 241002)

近年来，随着信息技术的飞速发展，全局优化技术在经济模型、图像处理、机械设计及环境工程等众多领域中受到广泛的应用。目前解决全局优化问题主要分为两个方面：进化算法(EAs)和基于群智能的优化算法。进化算法包括遗传算法(Genetic Algorithm，GA)、遗传规划(Genetic Programming，GP)、进化策略(Evolution Strategy，ES)和差分进化(Differential Evolution，DE)等改进算法[1]。群智能算法是一种模拟自然界生物群体行为来构造的随机优化算法，主要研究自然动物和昆虫的行为来解决问题。研究人员设计了模仿蚂蚁、蜜蜂的行为，以及细菌、萤火虫和其它生物的优化算法。创造这种算法的动力是不断增长的需求，以解决最优化问题。群智能算法具有清晰的结构、简单的操作和较强的寻优能力，可有效地解决一些传统优化算法无法在合理时间内解决的问题。主要群智能算法包括蚁群优化(the Ant Colony Optimization algorithm，ACO)[2]和粒子群优化(the Prticle Swarm Optimization algorithm，PSO)[3]等。目前，群智能算法已被广泛应用于自然科学、经济金融、医疗和工程技术等领域，并吸引了越来越多的研究者。

虽然蜘蛛已成为仿生工程领域的一个重要研究课题，然而大多数与蜘蛛相关的研究都集中在模仿其行走模式上。其主要原因是在大多数情况下人们观察到的蜘蛛都是独立活动的，不构成群居的特性。但是在科学家观察和描述的35000种蜘蛛中[4]，有些蜘蛛是具有群居性的，它们生活在一个群体中。针对这些群居的蜘蛛，James J Q Yu,et al[5]提出了一种模拟群居型蜘蛛搜寻食物行为的群智能算法，即社会蜘蛛算法(Society Spider Algorithm，SSA)。尽管SSA算法被提出的时间相对较短，但是James J Q Yu,et al通过对几组基准测试

函数进行仿真实验，证明SSA算法比ACO算法和PSO算法都具有较快的收敛速度，且能有效地避免早熟收敛和跳出局部最优值。但是SSA算法在高维复杂函数特别是在旋转多峰函数上的表现并没有优势。SSA算法采用随机游走的方式来保证种群的多样性，同时实现向最优状态的转移，从而限制了优化算法的收敛速度；另一方面，优化策略容易陷入局部最优值。

为了保证优化算法的全局收敛性，需要保证种群的多样性，加快收敛速度就会带来过早陷入局部最优值。为了提高算法的收敛速度并防止早熟收敛问题，提高全局优化效率，本文提出一种多群分层协作社会蜘蛛算法(Multi-swarm Hierarchical Cooperative Society Spider Algorithm，MHCSSA)基准测试函数[5-6]。仿真实验表明，运用MHCSSA算法的多群分层协作方法和主群的贪婪搜索策略在保证收敛速度的同时防止过早进入早熟收敛。

1 SSA算法描述与分析

1.1 SSA算法描述

SSA算法将优化问题的搜索空间作为一张多维的蜘蛛网，蜘蛛网上的每个位置表示一个可行的优化问题的j解决方案，所有可行的解决方案在蜘蛛网上都有相应位置。同时蜘蛛网也是蜘蛛产生振动的传输媒介。蜘蛛网上的每个蜘蛛都有其对应的位置信息和对应的适应值(位置信息基于目标函数计算产生，它代表了这个位置能找到食物的潜力)。蜘蛛在网上可以自由行走，当蜘蛛个体移动到新的位置时，它会产生振动在蜘蛛网上传播，每个振动都包含了一只蜘蛛的信息，其它蜘蛛在感应到振动后就会获得这些信息。每个蜘蛛个体通过判断自己位置的振动和感应来自其它蜘蛛传递来的信息来搜索食物，最终达到寻优目的。

1.2 蜘蛛个体

蜘蛛作为SSA算法执行优化的代理，在算法开始时，一群被预先定义的蜘蛛被放到蜘蛛网上。每个蜘蛛s都携带一些信息，存储以下内容：①蜘蛛s在蜘蛛网上的位置；②依据当前位置计算得到的适应值；③前一次迭代蜘蛛s获得的目标振动；④蜘蛛s最终改变其目标振动所经历的迭代次数；⑤前一次迭代蜘蛛s所执行的移动；⑥用于指导蜘蛛s在前一次迭代中运动的指导向量m。

前两类信息描述了蜘蛛个体的情况，而后几类信息涉及指导蜘蛛s移动到新位置。由于蜘蛛具有非常精确的振动感，同时它们可以在蜘蛛网上传递不同的振动并感应各自的强度。在SSA算法中，当蜘蛛到达一个新位置时，它会产生一个振动。振动会在蜘蛛网上传播，其它蜘蛛能够感应到这些振动，从而与其它蜘蛛分享个人信息，形成信息共享。

1.3 振动

振动是SSA算法区别于其它算法的重要概念。在SSA算法中，使用两种特征来定义振动，即振动的源位置和强度。源位置是由优化问题的搜索空间定义的。SSA算法定义了范围为[0，+)的振动强度。每当蜘蛛移动到新位置，会在此位置产生一个振动。定义蜘蛛个体a在时间t的位置为Pa(t)(或者简单表示为Pa)。同时定义I(Pa,Pb,t)为蜘蛛在时间t位置Pb感应到的来自位置Pa的振动强度，由此使用I(Ps,Ps,t)表示蜘蛛s在源位置产生的振动强度。源位置的振动强度与其位置的适应值有关，定义强度值为：

(1)

其中，C是一个比所有可能的适应值都小的常数；f(Pi)是根据目标函数和位置信息计算得到的适应值。

考虑到以下几个问题：①优化问题的所有可能振动强度都是正数；②有更好适应值的位置，即最小化问题的最小值，比较差的适应值的位置有更大的振动强度；③当解接近全局最优值时，振动强度不会过大增加。

定义蜘蛛a和b之间的距离为D(Pa,Pb)，SSA算法使用曼哈顿距离计算D(Pa,Pb)：

(2)

定义距离上的振动衰减：

(3)

其中，σ表示每个维度上所有蜘蛛位置的标准差，ra是控制距离的振动强度衰减率的参数，ra∈(0,)。

1.4 搜索模式

SSA算法有三个阶段：初始化、迭代和输出。这三个阶段按顺序执行，从初始化阶段开始，然后以迭代的方式执行搜索，最后终止算法并输出所找到的解决方案。

在初始化阶段，该算法定义目标函数及其解空间并设置参数，之后算法创建初始蜘蛛种群。由于在模拟SSA时，蜘蛛总数不变，所以分配一个固定大小的内存来存储它们的信息。在搜索空间中随机生成蜘蛛的位置，计算并存储它们的适应值。种群中各蜘蛛的初始目标振动被设置在其当前位置，且振动强度为零。每个蜘蛛存储的所有其它属性也用0初始化。初始化阶段结束后，算法开始进入迭代阶段，由创建的人工蜘蛛进行搜索。

在迭代阶段，算法执行多次迭代。在每次迭代中，蜘蛛网上的所有蜘蛛都移动到一个新位置，并评估它们的适应值。每一次迭代可以进一步分为以下几个步骤：适应度评估、振动生成、指导向量改变、随机游走和约束处理。

随后算法操作蜘蛛s朝vtar随机游走。使用维度向量m指导蜘蛛的移动。每个蜘蛛个体都持有一个维度向量m，它是一个长度为优化问题维度D的0-1向量，初始时m的所有值都为0。在每一次迭代中，蜘蛛s都有1-pc的概率改变m，其中pc∈(0,1)是一个用户定义的参数，用来描述改变m的概率。如果m被决定改变，向量的每个位都有pm的概率被设置为1，1-pm的概率被设置为0。pm∈(0,1)也是用户定义的参数。m的每一位都是独立改变的，与先前的值没有任何关系。如果所有位都为0，则掩码的一个随机值将更改为1。类似地，如果所有值都是1，则将一个随机位分配给0。

(4)

(5)

其中，⊙表示向量的乘法，R是和优化问题同维度的0-1向量。

迭代阶段循环直到停止条件匹配为止。停止标准可以定义为达到的最大迭代次数、所使用的最大CPU时间、达到一定错误率、最大迭代次数在最佳适应值上没有改进等。在迭代阶段后，算法以最佳适应度输出最优解。上述三个阶段构成了完整的SSA算法。

1.5 SSA算法分析

虽然SSA算法和粒子群(PSO)算法一样都是根据群体觅食行为设计的算法，但是两者确有明显的区别。

粒子群(PSO)算法同SSA算法一样，最初也是为解决连续优化问题而提出的,它也受到动物行为的启发。然而，SSA算法和PSO算法之间的第一个关键区别在于个体跟随模式。在粒子群算法中，所有粒子都遵循一个全局最优位置和各自的最佳位置。然而，在SSA算法中，所有蜘蛛跟随的位置都是由种群其它蜘蛛当前位置和自身历史位置构建的。此位置不能保证以前会被其它蜘蛛访问过，不同的蜘蛛可以有不同的跟随位置。由于全局最优位置和蜘蛛当前位置在优化过程的大部分时间内差异很大，这两种模式导致了不同的搜索行为。这可能削弱SSA算法的收敛能力，但有可能加强大量的局部最优解求解多峰优化问题的能力。

在信息传播方法方面,粒子群(PSO)算法与SSA算法也存在区别。在粒子群(PSO)算法中，信息传播方法被忽略，每个粒子被假定为知道系统所有信息而不损失。SSA算法是通过蛛网上的振动来模拟信息的传播过程，这个过程形成了一个具有信息损失的通用知识系统。

SSA算法在保持种群多样性和收敛速度的平衡上采用了蜘蛛个体朝着目标位置随机游走的策略。这种方法虽然能保证在一定收敛速度下种群多样性不会丢失，但是也在一定程度上限制了算法的收敛速度和处理局部最优值跳出早熟收敛的能力。

2 贪婪多群分层协作社会蜘蛛算法

2.1 MHCSSA算法描述

和大多数群智能算法一样，SSA算法同样也有种群多样性和算法收敛速度存在矛盾的现象。SSA算法的种群蜘蛛随机游走策略平衡了种群多样性的损失，使算法在跳出多个局部最优值方面表现突出。但是由此带来的是收敛速度的降低。贪婪多群分层协作社会蜘蛛算法(MHCSSA)在子群保持随机游走策略的基础上采用多群分层协作的思想来保持种群多样性。同时，蜘蛛个体根据划分的不同适应值范围分配到不同的分群中搜索，使得不同适应值水平的个体能公平地进行“捕食”竞争。

MHCSSA算法主要设置一个主群和数个子群[6]，子群的划分依据适应值范围分级划分。每个子群都依据其适应值范围设置一个移入阈值和移出阈值，移出阈值决定个体是否应该移动到更高适应值范围的子群或者主群中。下一级子群的移出阈值即为上一级子群的移入阈值。符合移入移出条件的个体同步或异步地跨越主群和子群。蜘蛛个体在子群间的移入移除如图1所示，并采取如下的搜索原则：

主群：主群中依据贪婪策略[7]，即指导蜘蛛向有前途的区域移动。当主群陷入早熟收敛，将局部最优的个体移出主群，移入到合适适应值范围的子群中。主群中的贪婪方法保证快速收敛。

子群：子群中依然依据标准的SSA进行搜索，若子群的蜘蛛个体适应值优于子群的移出阈值时，将此个体移出子群移入到更合适适应值范围的子群或主群中继续搜索。

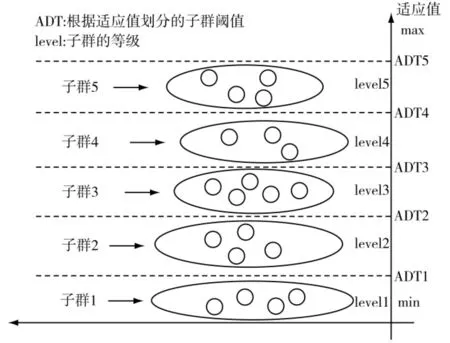
2.2 种群划分与层次结构

为了保证算法的全局收敛性，就要维持种群中个体的多样性，避免有效基因的丢失。为了加快收敛速度，就要使种群较快地向最优状态转移，这又会减少群体的多样性，容易陷入局部极值点。如何较快地找到最优解并防止早熟收敛问题是群智能算法中一个较难解决的问题。SSA算法在保持多样性上采取了蜘蛛随机游走的机制，这样就会限制收敛速度。MHCSSA算法采用多群划分的方式，且在子群中依然维持蜘蛛随机游走的机制来保证种群的多样性。

(6)

其中，Nl为分群的总数。由此得到主群的适应值范围[fmax,fmax-σf]、最低子群的适应值范围(-,fμ]和其余Nl-2个分群的适应值范围，每个子群的适应值范围的上限即为移出阈值，下限即为移入阈值。将初始化的种群体分配到合适适应值范围的分群中。

2.3 主群贪婪搜索策略

MHCSSA算法采用多群分层协作的思想保持了种群的多样性，且子群和SSA算法一样采用随机游走策略，大大降低了算法的收敛速度。采用种群分级划分方法，使算法在结束输出时依据主群搜索获得最优值。本文在主群中采用贪婪搜索策略来加快算法的收敛速度。

当主群中的蜘蛛个体接受到来自其它所有蜘蛛的震动后，其运动方式由随机游走变为指导其往振动最强的位置移动。同SSA算法类似,采用一个D维的0-1向量指导蜘蛛个体的移动，每个蜘蛛个体都持有一个运动向量，且每次迭代之后都会依据收到的种群最大振动强度的目标位置Ptar改变搜索方向。贪婪搜索移动后的新位置第i维值计算依据为：

(7)

其中，⊙表示向量的乘法，R是和优化问题同维度的0-1向量。

2.4 多种群分层协作

MHCSSA算法在主群中采用贪婪搜索策略来指导蜘蛛向有前途的位置移动而不是随机游走。这样虽然加快了算法的收敛速度，但是同样会带来早熟收敛的快速发生。当有蜘蛛个体发生早熟收敛现象时，则将此个体移出主群并移入到合适的适应值范围的子群中。多群分层协作主要采用如图3所示方法。分层协作的方法主要有两方面：①当主群的个体陷入早熟收敛后并不是立马移出主群，而是复制此个体存储的信息并按照其当前适应值大小判断哪个子群的适应值范围适合此个体移入。当找到合适的适应值范围的子群后则将此个体移出主群并移入到子群中。②当子群的个体适应值达到子群的移出阈值时，若此子群非最高级子群,则根据个体的适应值大小判断其移入哪个适应值范围的子群中，若此个体适应值优于最高级子群的移出阈值，则将其直接移入主群,否则移入到合适适应值范围的子群中；若此子群为最高级子群，则将个体直接移入主群中。

同SSA算法一样，MHCSSA算法分为初始化、迭代和输出三个阶段。MHCSSA算法是在SSA算法初始化阶段加入多种群划分从而达到种群的分层结构。在迭代阶段MHCSSA算法引入主群的贪婪策略和多种群分层协作的思想。MHCSSA算法的主体描述如下：

①设置算法参数，依据SSA方式初始化种群。

②依据种群初始的适应值降序排列，划分种群层次结构，并将种群个体分配到合适适应值范围的种群中，同时设置子群移入移除阈值。

While (不满足算法终止条件)

For蜘蛛个体in主群

③根据公式(7)对主群执行贪婪搜索策略，更新主群个体。

If (主群个体满足早熟收敛条件)

④将蜘蛛个体标记并复制其存储的信息。

End If

End for

For each子群

⑤根据公式(5)执行随机搜索，更新各子群个体。

For 蜘蛛个体in子群

If (个体适应值达到子群移出阈值)

⑥将蜘蛛个体标记并复制其存储的信息。

End If

End For

End For

⑦将标记的主群个体移出主群并移入到合适适应值范围的子群中。同步或异步地将子群中标记所有个体移出子群移入到合适适应值范围的子群或直接移入主群中。

⑧更新蜘蛛种群，更新蜘蛛子群移入移除阈值。

⑨迭代次数T=T+1。

End While

⑩输出结果，算法结束。

2.5 主群早熟收敛判断

对于复杂的实际优化问题，不能通过确定性分析来确定目标函数是否陷入局部最优点而早熟收敛。本文提出以下方法判定主群个体是否陷入局部最优点。

①利用种群适应值方差来判定蜘蛛个体的收敛程度。设主群规模为Nmain，fi为第i个蜘蛛个体的适应值，favg为平均适应值，σ2为种群适应值方差。

(8)

种群适应值方差σ2反应了蜘蛛群的个体密集程度，σ2越小，则表明算法越趋于收敛，反之则处于搜索状态。如果算法不满足终止条件，则σ2变小将使种群陷入局部最优值而导致早熟收敛。因此设定常数λ，当σ2<λ时标志主群陷入早熟收敛。

②个体平均适应值favg连续t1次迭代没有改变或者改变很小且不满足终止条件。

③全局最优fg_best值在经历t2次迭代后不改变或者改变很小且不满足终止条件。

3 实验仿真

为了验证MHCSSA算法的优化性能，在python仿真平台设置优化问题维度为50维，采用表1所示的10种基准测试函数[5-6]，比较MHCSSA算法和SSA算法的性能。同时将实验结果与其它优秀的超启发式算法，如自适应协方差矩阵进化策略算法(CMA-ES)[9]、特征矩阵联合近似对角化(JADE)[10]、自适应差分进化算法(SaDE)[11]和Global-Local实时编码遗传算法(GL-25)[12]等进行比较，这些超启发式算法都是在CEC 2013(Competition on Real-Parameter Single Ob jective Optimization Problems)中表现非常优秀的算法。它们主要用来测试MHCSSA与优秀的超启发式算法在优化问题上的竞争力。MHCSSA算法基础参数的设置和种群规模的大小同SSA设置相同。这些基准测试函数可被分为两组，其中f1～f4为单峰函数，f5～f10为多峰函数。单峰函数主要测试MHCSSA算法的快速收敛能力，而多峰函数由于有多个局部极值点，主要用来测试MHCSSA算法跳出局部最优点和防止早熟收敛的能力。所有的基准测试函数在0处取全局最小值,同时适应度下限取值为10-8 [5-6]。对所有基准测试函数独立运行100次来获取平均的全局最优值和迭代次数。

3.1 单峰函数对比实验

运用单峰函数组f1～f4来验证MHCSSA算法在50维度情况下的收敛速度。图4所示为单峰数组的函数收敛曲线，表2所示为实验的对比结果。

表2 50维度的单峰函数测试对比

从图4单峰函数实验结果中可以看出，MHCSSA算法的收敛速度明显快于SSA算法。特别是f2函数，MHCSSA算法仅需要少数迭代步骤即达到较小的目标值。比较f1和f3函数，迭代到10000代时，MHCSSA所得目标函数数量级优于103倍数。因为SSA算法在执行随机游走的同时进行搜索和开发，保持种群多样性和收敛精度的平衡，而MHCSSA算法在以多子群搜索结构保持种群多样性的基础上在主群采用贪婪搜索策略,使得MHCSSA算法在收敛速度上明显快于SSA算法。

从表2可以看出，在f1～f3结果中MHCSSA算法都能获得全局最优解。在f4的结果中MHCSSA算法获得了比SSA算法更好的结果，与CMA-ES算法和SaDE算法相比，MHCSSA算法有明显优势。虽然在f4实验结果中MHCSSA算法没有获得比JADE算法和GL25算法更优的结果，但是其结果却十分具有竞争力。

3.2 多峰函数对比实验

为了进一步验证MHCSSA算法跳出局部最优和避免早熟收敛的能力，在50维度情况下用多峰函数组f5～f10与SSA算法进行实验对比。图5所示为多峰函数组的函数收敛曲线，表3所示为实验对比结果。

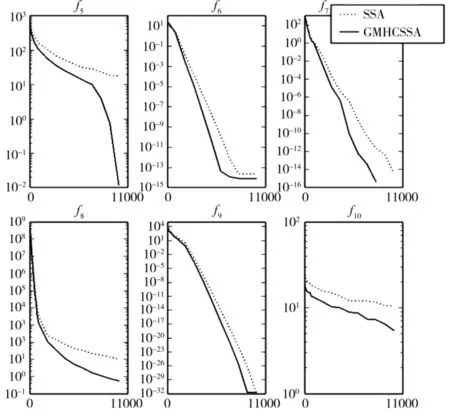
表3 50维度多峰函数测试对比

从图5所示的多峰函数实验结果可以看出，MHCSSA算法的收敛速度同样明显快于SSA算法。同时在跳出局部最优值和避免早熟收敛方面也比SSA算法表现出了更好的性能。因为SSA算法虽然在避免早熟收敛方面表现突出，但是SSA算法为了防止收敛精度的丢失和收敛速度的下降采用了随机游走的这种平衡两者的方式，使得在避免早熟收敛的方面受到限制。

从表3的实验结果数据可以看出，在f5、f6、f7和f9的结果中MHCSSA算法同其它算法一样获得了全局最优解。同时在f8的结果中，MHCSSA算法获得了比SSA算法更好的结果，且结果与JADE算法、SaDE算法和GL25算法表现同样优秀。虽然在f8实验结果中MHCSSA算法没有获得比CMA-ES算法获得更优的结果，但是其结果却并没有相差很多。在f10的结果中，MHCSSA算法结果比SSA算法、CMA-ES算法、SaDE算法和GL25算法都优秀，且与JADE算法结果十分接近。从整个实验结果可以看出，MHCSSA算法表现都比SSA算法更好，且在大多数情况下与其它优秀的超启发式算法表现同样优秀。虽然在函数结果中MHCSSA算法并不是最优秀的结果，但是与获得最好结果的超启发式算法结果非常接近，具有很强的竞争力。

4 结语

为了改进SSA算法在收敛速度和处理局部收敛方面的性能，本文提出了MHCSSA算法。通过多种群划分协作的方法保证了种群的多样性，同时在主群中引入贪婪搜索策略来优化算法快速收敛的能力。在主群中的个体达到局部最优情况时将被移出主群并移入到合适适应值范围的子群中，而子群的个体达到子群设置的移出阈值时将会被移入到更高级分群中，保证了算法避免局部最优和跳出早熟收敛的能力。仿真实验结果显示，MHCSSA算法的收敛速度和跳出早熟收敛能力比SSA算法表现更优。同时在与CMA-ES、JADE、SaDE和GL-25等算法比较时，MHCSSA算法在优化能力上同样表现得非常优秀，将会是非常有用的优化工具。