基于主成分与Adaptive-Lasso的飞机油耗统计分析

谭景宝，许 欢

(合肥幼儿师范高等专科学校基础部，安徽合肥 230013)

1 研究背景

现代航空运输是现代社会综合交通体系中的重要组成部分，是远程旅客选择出游的主要方式。随着经济的发展，国内外航空运输正迅猛发展，大部分人在国际国内远程旅行时选择乘坐飞机，并且乘客人数每年都在增长。燃油流量被视为飞机发动机重要的技术参数之一，它直接影响飞机性能的优劣，反映发动机性能衰减的状况。为此，各大航空公司采取各种措施来提高燃油效率，以减少不必要的燃油成本。飞机在飞行过程中的燃油消耗受到多种因素的影响，建立燃油消耗模型，利用模型对飞机燃油流量进行监控，对提高燃油效率有着重要意义。

目前已有大量学者对飞机燃油消耗模型进行了研究。王伟[1]、Bela P C[2]、傅职忠[3]分别基于能量守恒原理的燃油消耗和基于实际非参数据的传统统计以及基于智能算法建立模型，并对模型进行分析；Trani A A[4]、刘婧[5]、刘芳[6]分别基于非参数数据的神经网络方法，建立了燃油消耗回归预测模型，提高了飞机燃油消耗的预测精度。王长坤[7]基于真实飞行QAR数据,采用两阶段分析，第一步找到影响飞机飞行的燃油消耗的因素，第二步利用多元线性回归分析方法，建立飞机飞行燃油流量模型；耿宏[8]在深入分析飞机飞行QAR数据的基础上，确定了影响飞机燃油流量的因素，基于多元线性回归分析建立飞机燃油消耗回归预测模型，并利用该模型对飞机燃油消耗进行了预测分析；杨姝[9]利用灰色关联分析法找出了影响飞机油耗的因素，并基于多元线性回归方法在挑选出的一组相关性强、结构合理的要素和耗油量间构建了燃油消耗量模型。

在飞机油耗的研究中，通常采用线性回归方法，建立线性回归模型，利用最小二乘法估计模型的参数。但在现实中，对某些情况如变量间存在严重的多重共线性时，该种方法的估计值并不准确，从而导致预测精度较低。此外，当影响因素即自变量数量较多时，对模型的解释能力就会降低。1996年，Tibshirani R[10]提出了Lasso方法，目的是为了压缩模型参数，使得某些回归系数变小。之后，很多学者提出了Lasso方法的改进技术，并利用Lasso方法进行多元统计分析。谭常春[11]基于Adaptive-Lasso方法，建立了城市火灾次数与气象因素的回归模型，很好地预测了城市火灾次数；谭常春[12]在主成分分析的基础上运用Adaptive-Lasso方法分析了本科课程对本科成绩的影响，建立了回归模型并预测了后期成绩。

本文针对2014-04-08至2015-04-09飞机飞行阶段耗油量，分析飞行速度、高度、气温、风速、重量、经度等相关的因素对其的影响，分别用主成分分析方法与Adaptive-Lasso方法进行建模。并对以上两种模型进行分析比较，最终显示，通过Adaptive-Lasso方法建立的回归模型能更好地拟合飞机耗油量。

2 主成分与Adaptive-Lasso方法介绍

2.1 主成分模型

主成分分析方法(Principal Component Analysis，PCA)采用降维的思想，通过正交变换将一组存在相关性的多个指标转换为一组线性不相关的少数几个综合指标，少数的几个综合指标代表了总体的大多数信息，我们称之为主成分。它是将众多指标进行综合，消除样本间的信息重合，消除共线性，综合后的少数指标彼此间互不相干，且保留了尽量多的原始变量信息，即利用少数的几个指标来揭示原始变量间的内部关系。通常的处理方式就是将原始变量进行线性组合，组合后的变量作为新的综合指标。其模型为：

2.2 Adaptive-Lasso方法

Lasso利用压缩估计的思想，是一种将变量的选择和参数的估计同时进行的方法，其参数估计为：

其中，λ为非负正则化参数，β=(β1,β2,…,βk)T是回归系数，Xj=(x1j,x2j,…,xmj)T，j=1,2,…,k是预测变量，X=(X1,X2,…,Xk)是预测变量矩阵，Y=(y1,y2,…,ym)T是响应变量。

构造惩罚函数，压缩变量的系数，是Lasso方法的关键。随着λ的增加，Lasso方法使得系数连续地趋向于0。当λ足够大时，系数被压缩到0。系数连续的缩小使得偏差被权衡掉，从而提高了模型预测的精确度。

Lasso方法虽然可以解决普通最小二乘和逐步回归中变量共线性的问题，但需在满足一定条件的情况下。我们选用一个改进的Lasso方法，称为Adaptive-Lasso方法，其改变的地方在于给不同的系数分配不同的权重。定义如下：

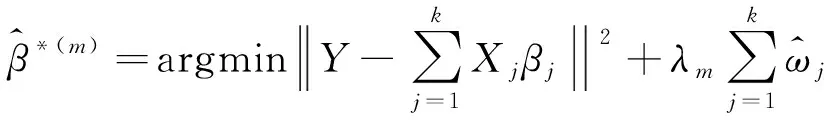
3 主成分分析

本文中所使用的数据为某家航空公司2014-04-08至2015-04-09飞机飞行阶段的耗油量数据,如表1所示。

表1 飞机耗油量及其因素

因因素太多表中不能全部列举，故省略一些因素，省略的有：地速、计算空速、马赫、重量、经度、纬度、总温、静温、耗时(ACCUM)、地速距离(ACCUM)、空速距离(ACCUM)。

将上述1252组数据中的前1052组数据进行分析，对后200组数据进行预测比较。对前1052组数据中的飞行速度、高度、气温、风速、重量、经度等相关因素进行主成分分析，建立回归模型。

主成分分析结果如表2所示，共有9个主成分。

表2 主成分分析成分贡献率

采用前4个主成分进行回归分析，累计贡献率大于70%。第一主成分与第三主成分主要为客观环境变量，包括高度、真空速、经度、维度、总温及静温，其贡献率分别为26.9%、15.5%；第二主成分主要为飞机飞行变量，包括地速、耗时、地速距离和空速距离，其贡献率为18.8%；第四主成分主要为飞机自身变量，包括重量、马赫等，其贡献率为14.1%。

利用主成分分析所得的成分矩阵，采用逐步回归法建立飞机油耗与主成分之间的回归模型，结果如表3所示。

表3 逐步回归法回归系数

注：***表示结果显著。

由此得出回归模型：

y=30.089+0.137Comp1-6.069Comp2+1.282Comp3-0.895Comp4.

此回归模型的拟合优度为0.9569。

对后200组数据根据以上模型进行预测，并将预测数据与实际数据进行比较，如图1所示，其中横轴代表数据序号，纵轴代表油耗，实线代表实际值，虚线代表预测值。

其均方误差为123.252，从图1看出，预测值与实际值走势大致吻合，但在30～50和150～180这两段误差较大。

4 Adaptive-Lasso回归

将上述1252组数据中的前1052组数据进行分析，对后200组数据进行预测比较。利用Adaptive-Lasso建立飞机油耗与相关因素之间的回归模型，表4为各相关因素的回归系数。

表4 Adaptive-Lasso方法回归系数

由表4可以看出，Adaptive-Lasso方法剔除了一些共线性的变量，如经度、维度等，保留了温度、静温、耗时、空速距离4个变量，其相关检验如表5所示。

表5 相关检验

注：***表示结果显著。

由此得出飞机油耗与相关因素之间的回归模型：

y=-5.009+0.072X7-0.008X9+0.086X10+5.067X11.

模型拟合优度为0.9736，大于基于主成分分析的回归模型的拟合优度。因此得出结论，基于Adaptive-Lasso方法的回归模型要优于基于主成分分析的回归模型。

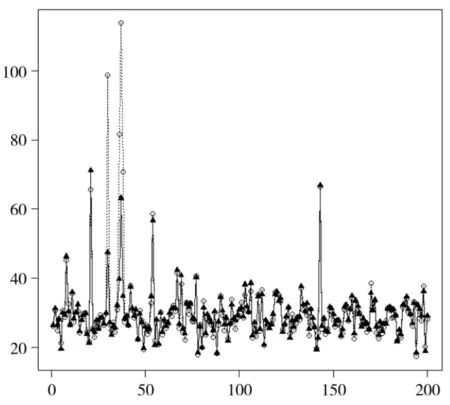
对后200组数据根据以上模型进行预测，并将预测数据与实际数据进行比较，如图2所示，其中横轴代表数据序号，纵轴代表油耗，实线代表实际值，虚线代表预测值。

其均方误差为44.262，从图2可以看出，预测值与实际值基本吻合，说明拟合效果较好。与基于主成分分析方法建立的模型相比，通过Adaptive-Lasso方法建立的回归模型能更好地拟合飞机耗油量。

5 结语

本文根据2014-04-08至2015-04-09飞机飞行阶段耗油量及飞行速度、高度、气温、风速、重量、经度等相关的因素，分别建立了主成分逐步回归模型和Adaptive-Lasso回归模型。经过对比分析后可得，主成分逐步回归虽然保证了较好的模型解释和预测精度，但模型的拟合度不如Adaptive-Lasso方法建立的回归模型。但从实际考虑，Adaptive-Lasso方法剔除了较多的变量，仅利用较少的变量进行拟合，其模型解释性不高，没有很好的实际意义。由回归模型可以得出，飞机飞行的耗油量是由客观环境、飞机自身及飞机飞行三者共同决定，并且环境对其影响较大，航空公司可适当根据环境调整飞行状态，以减少油耗。