一种求解低秩矩阵填充问题的新方法
2018-08-17王燕荣尹佳杰闫喜红
王燕荣,尹佳杰,闫喜红
(太原师范学院 数学系,山西 晋中 030619)
0 引言
低秩矩阵填充问题是指,主要研究的是在已知采样矩阵部分元素的前提下,合理精确地填充一个低秩矩阵,此类问题已经成为了图像恢复[1]、人脸识别[2]等信息科学领域和工程领域关注的焦点.其数学模型为:
(1)
其中X,D∈Rm×n,PΩ(D)是已知的矩阵,Ω是所有已知元素的下标集合,PΩ(D)是Ω的正交投影.问题(1)是一个典型的非凸问题.Candes和Recht[3]提出低秩矩阵可以通过解决如下的凸优化问题实现矩阵的填充:
(2)

对于求解模型(2)的算法Wang等人最近提出了两种简单且高效的算法来解决低秩矩阵的填充问题.这两种算法的基本理论依据是当r固定时,在r维流形上用标准的SVD或最小二乘法找到最优的可行矩阵.并且逐步更新流形的维数,即更新矩阵的秩,实现可行矩阵收敛于问题(1)的最优解.
但这两种算法本质上都是对矩阵的秩采用逐步加一的方法进行更新,这样导致收敛最优解的速度较慢.本文用割线法更新秩,从而建立一种求解低秩矩阵填充问题的新方法,并通过数值实验验证了新方法的有效性.
1 相关算法介绍[4]
1.1 算法1:最优低秩矩阵近似(OLRMA)算法
1.2.1 基本理论依据
在r维流形上可行矩阵和它的投影之间的距离:
(3)
结合模型(1)和模型(3),当r
1.1.2 算法1的具体步骤
第一步:首先给定下标集合Ω,样本元素PΩ(D),参数0 第二步:计算矩阵YK的SVD:[Uk,Σk,Vk]=lansvd(Yk,r,L); 第三步:令Xk=Uk∑kVkT; 第四步:如果‖PΩ(D)-PΩ(Xk)‖F≤‖PΩ(D)‖F,rk+1=rk否则rk+1=rk+1; 第六步:判断‖PΩ(D)-PΩ(Xk)‖F/‖PΩ(D)‖F≤ε.如果成立,停止,否则转到第二步. 输出矩阵Yk. 1.2.1 基本理论依据 (4) 这样的解决方案将比算法1更加接近最优解,显然,这将会是解决优化问题(4)的时间.在算法2中给出了主要的步骤,对(4)的一致性进行了重写(见步骤三),d和mi分别是矩阵PΩ(D)和矩阵PΩ(Mik)的向量形式,而且Mik=(m1k,m2k,…,mrk)是它等于所观察到的条目总数的大小. 1.2.2 算法2的具体步骤 第一步:首先给定下标集合,样本元素P(D),参数0 第二步:计算矩阵YK的SVD:[Uk,Σk,Vk]=lansvd(Yk,r,L); 第五步:如果‖PΩ(D)-PΩ(Xk)‖F≤‖PΩ(D)‖F,rk+1=rk否则rk+1=rk+1; 第七步:判断‖PΩ(D)-PΩ(Xk)‖F/‖PΩ(D)‖F≤ε.如果成立,停止,否则转到第二步. 在算法1和算法2中,在每次更新流形的维数上采用逐步加一的方法,这种方法虽然能够保证所求的矩阵是低秩矩阵,但这种方法,对于更新流形的维数比较慢,特点是当目标矩阵的秩比较大时,运行时间较长,效率较低.针对以上算法中的缺点,我们提出了流形维数的新方法. 基本理论是把误差看成是流形维数的函数,利用割线法寻找最优的流形维数.把这种思想结合算法1和算法2,形成如下新的算法3秩更新的最优低秩矩阵近似(OLRMA2)算法和算法4秩更新优化的最优低秩矩阵近似基于 (OLRMAO2)算法. 2.2.1 算法3的具体步骤 第一步:首先给定下标集合,样本元素P(D),参数0 第二步:计算矩阵YK的SVD:[Uk,Σk,Vk]=lansvd(Yk,r,L); 第三步:令Xk=Uk∑kVkT; 第四步:如果‖PΩ(D)-PΩ(Xk)‖F≤‖PΩ(D)‖F,rk+1=rk.否则令 第六步:判断‖PΩ(D)-PΩ(Xk)‖F‖PΩ(D)‖F≤ε.如果成立,停止,否则转到第二步. 得到的矩阵Yk就是我们需要的矩阵. 2.2.2 算法4的具体步骤 第一步:首先给定下标集合,样本元素P(D),参数0 第二步:计算矩阵Yk的SVD:[Uk,Σk,Vk]=lansvd(Yk,r,L); 第五步:如果‖PΩ(D)-PΩ(Xk)‖F≤‖PΩ(D)‖F,rk+1=rk; 第七步:判断‖PΩ(D)-PΩ(Xk)‖F/‖PΩ(D)‖F≤ε.如果成立,停止,否则转到第二步. 针对随机矩阵的矩阵填充,对两种算法(将割线法更新秩的算法和Wang等人的算法)进行比较,所有数值实验语言的编写使用软件Matlab7.0. 表1和表2中可以看到在矩阵维数n较小的时候,割线法更新秩的新算法所需要的时间和效率比原来的算法要好;当n逐渐增大时,割线法更新秩的弊端逐渐显示出来,时间和效率都略微低于原先的算法. 当矩阵的秩r较大的时,割线法更新秩的算法需要的时间比原算法要少;但当矩阵的秩r较小时,割线法更新秩的算法需要的时间比原算法要多. 表1 算法1和算法3随机矩阵填充问题的数值结果 表2 算法2和算法4随机矩阵填充问题的数值结果 本文首先用割线法更新秩的方法来得到新的算法.然后对随机矩阵的矩阵填充进行了数值实验.实验结果显示:割线法更新秩的算法在矩阵较小的时候,在准确性和效率上都比原先的算法要好;对秩较大的矩阵填充问题,割线法更新秩的算法显示其本身具有的优越性.但是对于大型矩阵的填充,割线法更新秩的算法还有待进一步改进.
1.2 算法2优化的最优低秩矩阵近似基于Ω(OLRMAO)算法
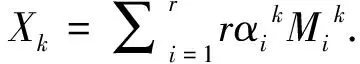
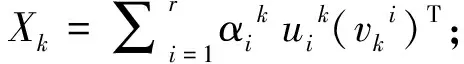

2 新算法的提出
2.1 基本理论依据
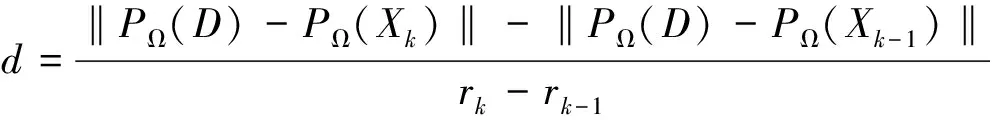




3 数值实验


