三割线定理的本质与运用

江苏省东南大学(211189)徐文平

侯明辉老师运用三角函数方法证明了三割线定理[1],在平面几何中圆类问题的计算和论证方面有着广泛的应用,依靠这个定理解题的步骤可以大大的简化.下文笔者依据极点和极线性质,探寻三割线定理的本质,并拟推广到圆锥曲线之中,验证圆锥曲线三割线定理的正确性,开展三割线定理的运用讨论,供大家鉴析.

一、关于三割线定理的本质

1.三割线定理简介

定理1PAB、PCD为圆的任意二条割线,AD与BC交于点Q,PQ连线与圆交于点E、F点,则PQ调和分割

图1

2.极点极线方法作椭圆切线

1)勒姆柯尔方法

勒姆柯尔过椭圆外一点P,引四条割线PAiBi(i=1,2,3,4),直线A1B2与A2B1交于Q点,直线A3B4与A4B3交于R点,直线QR交椭圆于S、T两个点,则S、T是椭圆对应点P的两个切点,直线PS、PT就是所求的切线(图2).

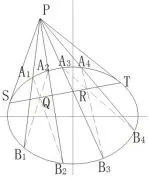
图2

2)舒马赫方法

大数学家高斯的朋友舒马赫不满足勒姆柯尔的方法,写信给高斯,信中说他找到了一个只需引三条割线就可以作椭圆切线的方法.(图3).

图3

3)高斯方法

高斯在收到舒马赫的信第六天,回信提出了一个只需引两条割线.就可以作椭圆切线的简捷方法(图4).

图4

3.三割线定理的本质

勒姆柯尔、舒马赫和高斯三人提出的椭圆切线作图方法均为极点极线方法,依据极点P探寻极线ST上的二点Q、R,连接QR直线交椭圆于S、T二个切点,即PS和PT为二条切线.

依据射影几何知识可知,图4中三角形PQR是自配极三角形,其中P极点的极线是QR极线,可用于寻找ST切点,R极点的极线是PQ极线,Q极点的极是PR极线.

在图1中,三割线定理中的P、Q二点就是极点P和极线上一点Q的对应关系,三割线定理的本质就是过椭圆外一点P作任意割线PEF交圆于E、F二点,割线PEF交极点P的极线于Q点,则P、E、Q、F形成调和点列.

二、简明的三割线定理的证明方法

1.三割线定理的纯几何证明

引理1从圆外一点P,引圆的两条切线和一条割线,S、T为切点,A、B点为割线与圆的交点,切点弦线ST与PAB割线交于Q点,那么PQ调和分割AB.

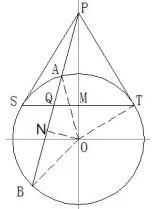
图5

证明如图5,假设N点为AB的中点,分析得知,AB⊥ON,所以Q、M、N、O四点共圆,则PQ·PN=PM·PO.因为△POT与△PMT是相似三角形,PT2=PM·PO.因为PT2=PA·PB,所以PQ·PN=PA·PB.因为所以PQ·(PA+PB)=2PA·PB.所以所以PQ调和分割AB.

引理2从圆外一点P引两条切线,得到两个切点S、T点,从圆外一点P引两任意割线,与圆交于A、B与C、D四点,交叉连接AD、BC直线交于Q点,AC与BD延伸交于R点,则S、T、Q、R四点共线.(高斯配极三角形命题)

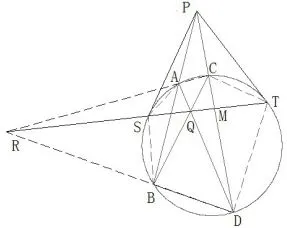
图6

证明联结AS、SB、BD、DT、TC、CA直线,得圆内接的凸六边形ASBDTC.欲证S、Q、T三点共线,只需证明AD、BC、ST三线共点.对于圆内接凸六边形ASBDTC,利用塞瓦定理,只须证明因为△PBD∽△PCA,△PTC∽△PDT,△PAS∽△PSB,则又因为PS=PT,所以所以因此,BC、AD、ST三线共点,S、Q、T三点共线.在三角形△RCD中,假设M点为RQ与CD的交点,由赛瓦定理得因为△RCD被直线PB所截,由梅涅劳斯定理得：将上面两个式子相乘得：所以CD被PM调和分割,同时PM被CD也调和分割.依据引理1可知,M点在极线ST上,所以M、R、S、T四点共线,所以M、S、T、Q、R五点共线,因此S、T、Q、R四点共线.

三割线定理简证

图1中,PAB、PCD为过椭圆外一点P引出的两条任意割线,AD与BC交于Q,直线PQ交椭圆于E、F二点.由引理2可知,AD与BC交于Q,则Q点在以P点为极点的ST极线上.由引理1可知,因为Q点在ST极线上,则PQ调和分割EF,即因此,对于在圆的情况下,三割线定理成立.如图7,依据坐标线性变换原理,圆转换为椭圆,直线段仅是线性变换其位置,线段比例关系不变,因此,对于在椭圆的情况下,三割线定理也成立.

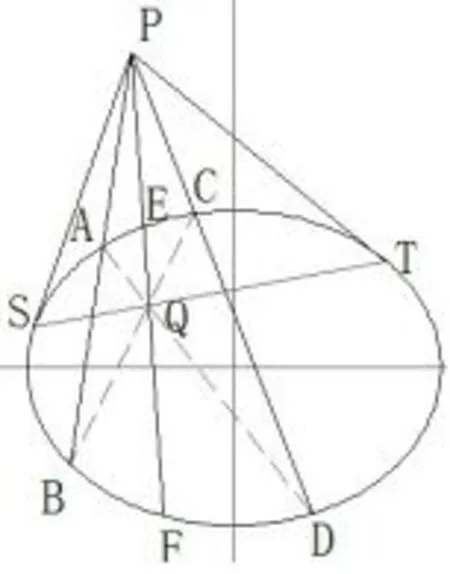
图7

2.圆锥曲线三割线定理的极点极线方法证明

引理3(完美四边形的调和性质)如图8中,完美四边形ABCDEF有三条对角线AC、BD和EF,则一条对角线的两端点必定调和分割该对角线与另两条对角线的两个交点.即：EF调和分割MN;BD调和分割KM;AC调和分割KN.

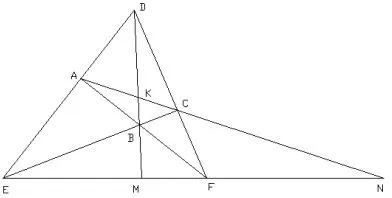
图8

简证由于AF、EC和DM三线共点B,由赛瓦定理得：又直线ACN截△DEF,由梅涅劳斯定理有EF调和分割MN.类似可证：BD调和分割KM;AC调和分割KN.

引理4(圆锥曲线三割线定理)极点P与对应极线上任意一点Q调和分割该两点连线与圆锥曲线相交的A、B两点.如图9,已知椭圆外一点P,作两条切线PS和PT,连接ST极线.作割线PAB,且该割线与ST交于点Q,则A、B调和分割线段PQ.即

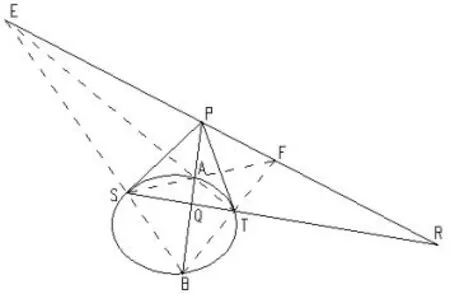
图9

证明由帕斯卡定理可知,EPF三点共线,EF为Q点的极线,图8形状成立.依据完美四边形ASBTEF的基本特性可知,E、P、F、R四点调和分割,EF调和分割PR.由射影几何知识可知[2],以B点为射影点分析S、Q、T、R四点连线,ST调和分割QR.由射影几何知识可知,以E点为射影点分析B、Q、A、P四点连线,AB调和分割PQ.依据极点与极线的对偶性,如果P点在椭圆内部,任意选取极线上一点Q,引理3也成立.

采用射影几何思想用于圆锥曲线,可得到许多新颖的结果.大数学家笛沙格采用一种有效的方法—投射取截法来实现二次圆锥曲线的连续变化.只要改变截景平面的位置,就可使圆的截景从圆连续变为椭圆、抛物线和双曲.因此,对于圆成立的许多性质,都可通过取截景的方法来证明它们对其他二次圆锥曲线也成立.这就提供了一种相当简便的方法.

因此,同理采取类似构图方法,可以快速证明双曲线和抛物线中,引理4也成立.

如图10,抛物线外一点P,作割线PAB和PCD,BC和AD交于点Q,连线PQ交抛物线于E、F点,则PQ调和分割EF,即

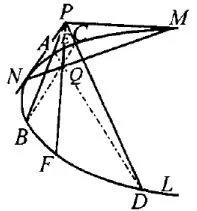
图10

三、关于三割线定理的运用

1.简化解题

例1圆I是三角形ABC的内切圆,圆I切BC边于D点,AD交圆I于M点,过M、D两点的圆I的切线交于P点,E是DM上的一点,BE、CE分别交圆I于G、F两点,求证：MP、DP、GF三线交于P点.

图11

在图11中,从P点作一个割线PFG,交AMD于Q点.极点P与极线AMD相对应,依据三割线定理,则G、Q、F、P四点调和.依据题意可知：B、D、C、P四点调和分割.(详见补证1)依据射影几何原理,E点是射影点,则BG、DM、CF交于一点E,证明完毕.

补证1如图12中,假定S、T为切点,圆I是三角形ABC的内切圆,则,AS=AT,BS=BD,CD=CT,即：切线长度相等.利用比赛瓦定理,可以证明AD、BT、SC三线交于一点R,由于A、M、D三点共线,依据极点与极线对偶性,则ST、MP、DP交于一点P,分析ASRTBC完美四点形,可知,BC调和分割DP,B、D、C、P四点调和分割.

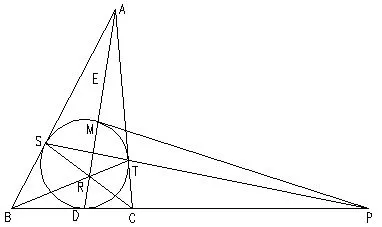
图12

2.尺规作图做椭圆的切线

例2(过椭圆上一点作切线)如图13,取AB的中点M,连接MO,延伸与椭圆交于C、D两点,作CD为直径的圆,作MP垂直于CD,过P点作圆切线,CD与切线PN交于N点,则极线AB的极点为N点.(原理：MN调和分割CD),证明略.

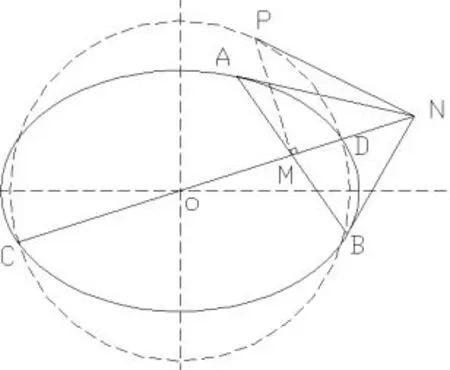
图13

例3(过椭圆外一点作切线)如图14,连线OM,交椭圆于C、D两点,作CD为直径的圆,过N点作圆的切线,切点为P点,作PM垂直CD,过C点作椭圆的切线,过M点作切线的平行线交椭圆于A、B两点,则AB为极线.(原理：MN调和分割CD),证明略.

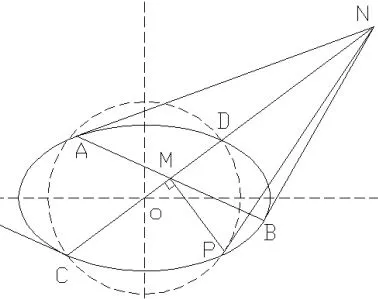
图14

3.证明六点共椭圆

利用帕斯卡定理或者卡诺定理证明六点共椭圆常常是非常复杂有难度,然而,利用完美四边形获得四点调和分割条件,依据极点极线对偶性质,再利用三割线定理的调和分割性质,就可以判定六点共椭圆,事半功倍效果,屡试不爽.

例4在椭圆外任意一条直线上,任意选取四点,过四点作椭圆的切线,形成二个外切椭圆的牛顿四边形,则二个外切牛顿四边形的八个顶点共椭圆.

如图15,牛顿四边形ABCD外切小椭圆,Q点为极点,XY为极线.在极线XY上,任意选取二点M和N,做小椭圆的切线,形成新的四边形EFGH,则二个外切四边形ABCD和外切四边形EFGH的八点共椭圆.

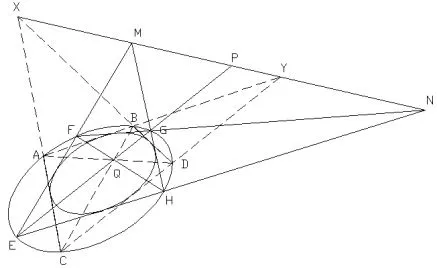
图15

简证运用牛顿几何定理3,由极点和极线性质可知,新构成的牛顿四边形EFGH对角线也是交于极点Q,假设四边形ABCD加上一点E点,可以构成一个外椭圆(五点定椭圆).由完美四边形EFGHMN可知,PQ调和分割EG.由三割线逆定理可知,PQEG满足调和分割条件,则G点也在外椭圆之上,即ABCDEG六点共椭圆.同理,也可以证明ABCDFH六点共椭圆.因此ABCDEFGH八点共椭圆.同时,也完成了彭色列闭合定理(N=4)证明.