八次软物质准晶圆柱绕流的动力学分析

2018-08-17范天佑

太原师范学院学报(自然科学版) 2018年2期

王芳,范天佑，成惠,3

(1.朔州师范高等专科学校自然科学系，山西朔州 036002；2.北京理工大学物理学院，北京 100081；3.河北工程大学物理系，河北邯郸 056038)

0 引言

本文建议的软物质准晶的动力学数学模型，解决了关于软物质准晶圆柱绕流的动力学问题.对于复杂的边界问题，只有为数很少的情况可以通过解析法[1]求得近似的解.尽管仅仅是近似，但对于理解软物质准晶的动力学特性仍有一定的意义.然而，这里讨论的是八次软物质准晶的圆柱绕流，由于方程组与初边值条件的复杂性，此问题只能用数值法求解，而且计算结果较解析法更为精确.与12次软物质准晶的圆柱绕流[2]不同，8次软物质准晶的声子-相位子耦合，计算结果展示了其更丰富的流动特性，其中，相位子发挥了很重要的作用.

1 极坐标系下的Oseen修正的动力学方程组

根据8次软物质准晶的动力学方程组[3]，推导出极坐标系下8次软物质准晶的Oseen修正[4]后的动力学方程组的一般形式.

因此，8次软物质准晶[3]的终态控制方程在极坐标下转化为

(1)

其中，方程组(1)的最后一式是状态方程，只有加入此方程，方程组(1)才满足封闭性.

2 圆柱绕流模型

此部分将软物质准晶的动力学数学模型推广应用到圆柱绕流的问题.如图1所示，从无限远处有一速度为U的来流沿x轴流动.

图1 软物质准晶以半径为a的圆柱绕流

无限远处压强p忽略不计，在无限大的软物质准晶中有一横截面半径为a的圆柱.在柱坐标(r,θ,z)下，边界条件有，

Vr=Ucosθ,Vθ=-Usinθ,σrr=σθθ=0,Hrr=Hθθ=0,

r=a:

Vr=Vθ=0,σrr=σrθ=0,Hrr=Hrθ=0.

(2)

初始条件为

t=0:

Vr=0,Vθ=0,ρ=ρ0,ur=uθ=0,wr=wθ=0.

(3)

3 有限差分法求解

由于方程组(1)很复杂，加之初边值条件(2)和(3)比较特殊，目前无法得到其解析解，通过数值法求解，考虑用极坐标下的有限差分法[4]，差分网格如图2所示.

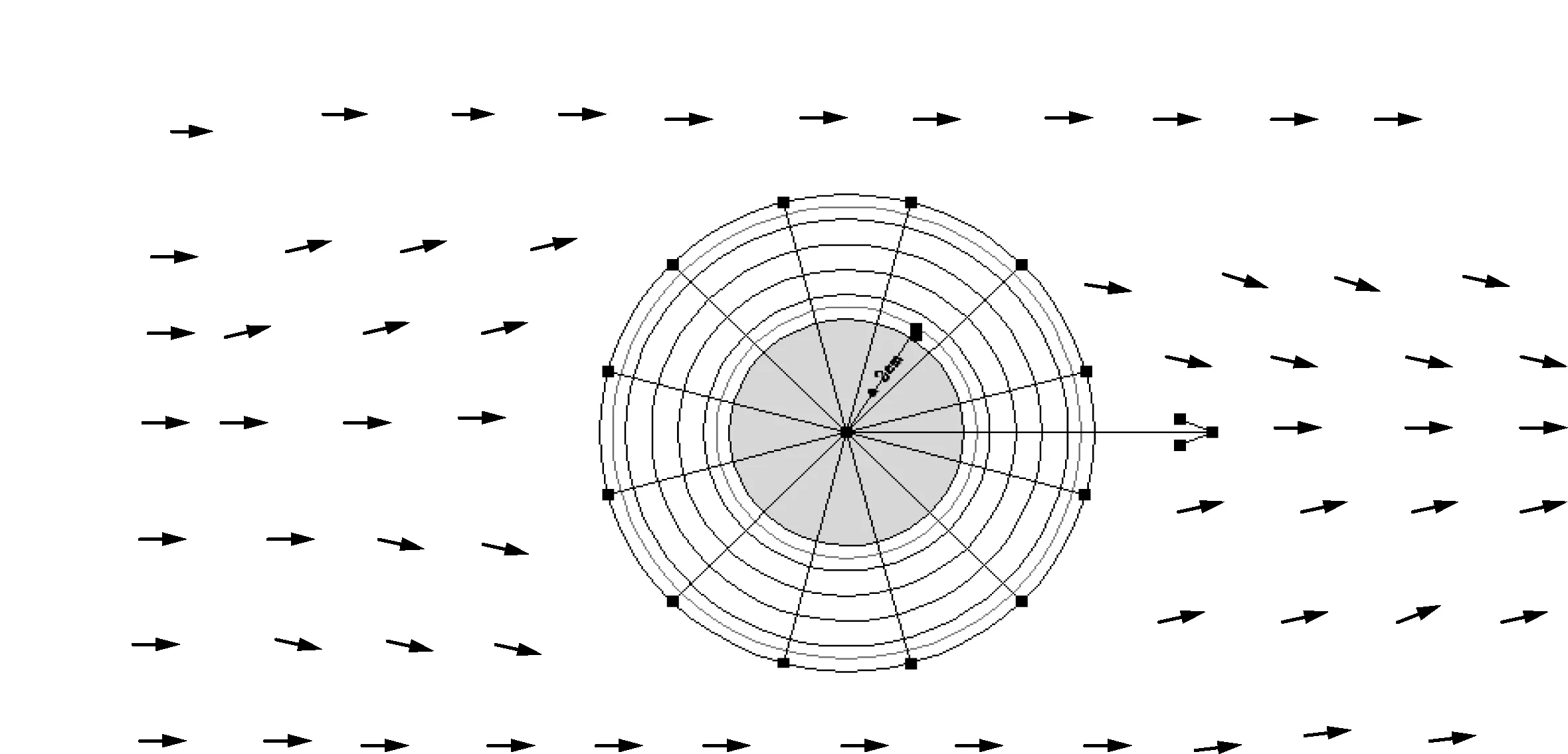
图2 极坐标系下的差分网格

4 数值结果及分析

在数值计算中，用到的材料常数和几何参量[4]为，U=0.01 m/s,ρ0=1.5 g/cm3,η=1Poise,l=7～8 nm,r/a=1.55,a=1 cm,kB=1.38×10-23J/K,T=293K,L=10 MPa,M=4 MPa,K1=0.5 L,K2=-0.1 L,B～0.2 MPaK3=0.05 L,Γu=4.8×10-17m3·s/kg,Γw=4.8×10-19m3·s/kg,A～0.2 MPa,声子-相位子耦合弹性常数为R=0.04 M.

图3～图6给出了速度和声子应力，相位子应力、流体黏性力的角分布，图形规则，物理规律较明显.其中，图3(a)，3(b)分别是圆柱外一定距离r/a=1.55处流体的径向速度vr与轴向速度vθ的角分布.因为软物质准晶有多个元激发，受声子场、相位子场及流体声子场相互作用的影响，速度要小于以普通流体为介质的速度.

图4分别给出了声子应力σrr,σθθ,σrθ的角分布，这些结果只有软物质准晶有，对于普通流体并没有声子场元激发，因此也没有声子弹性应力.

图3 r=1.55a处速度的角分布

图4 r=1.55a处，声子应力的角分布

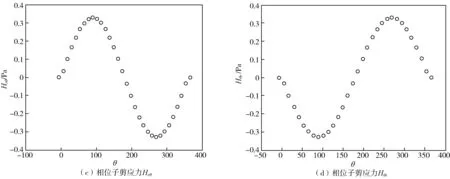
图5 在r=1.55a处，相位子应力的角分布

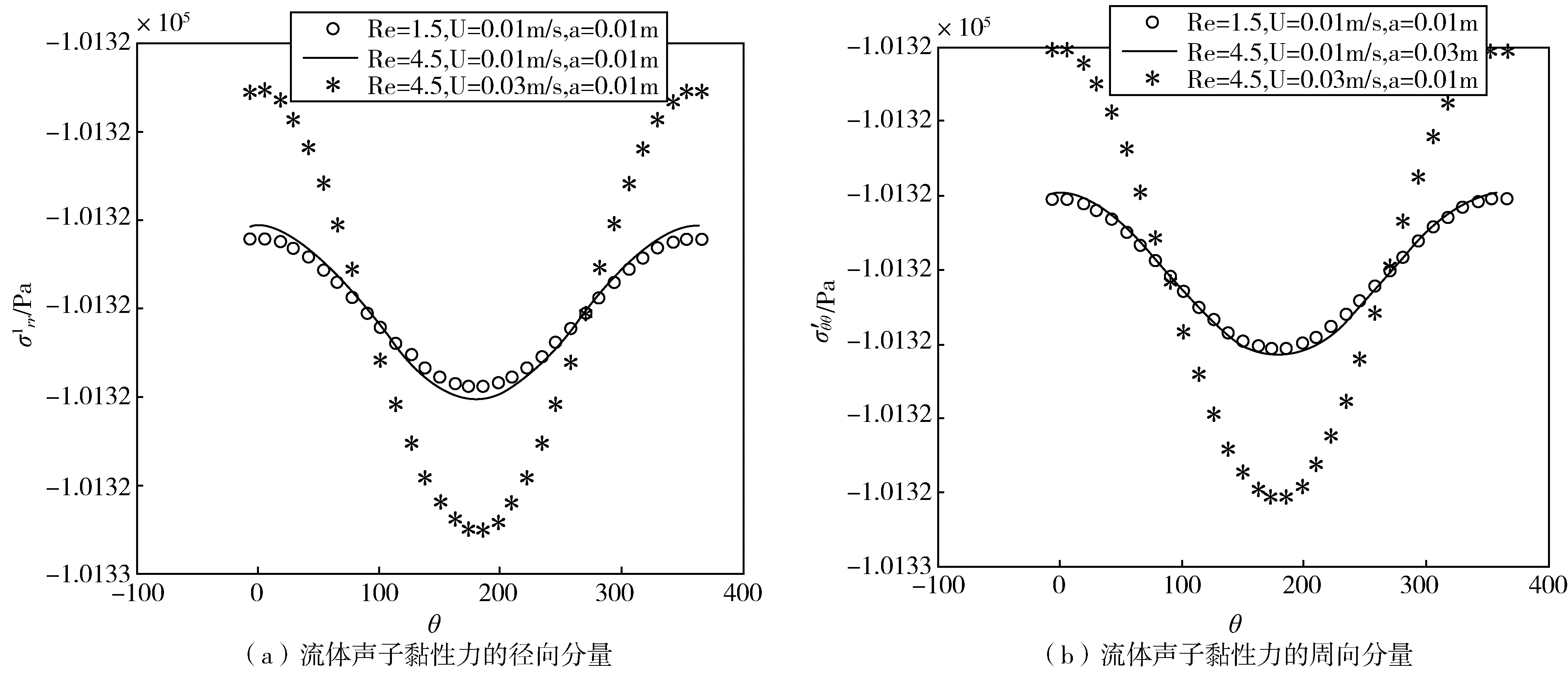
图6 r=3.55a处，在不同雷诺数下流体声子黏性力的角分布

特别注意的是，与12次[2]相比较8次软物质准晶的圆柱绕流的计算结果里增加了相位子应力，如图5所示，Hrr,Hθθ,Hrθ,Hθr分别是相位子应力的径向，周向及两个剪应力分量(相位子应力场Hrθ≠Hθr).这是因为与12次软物质准晶不同，8次软物质准晶存在声子-相位子耦合，这也是8次软物质准晶与12次软物质准晶最大的区别，其更深层次的物理机制有待进一步探索.

图6显示了流体应力在不同雷诺数、不同来流速度和不同柱半径下的角分布，从图6(a),6(b),6(c)看出，雷诺数Re，来流速度U，柱半径a都会显著影响流体应力的大小，因此，雷诺数在流体动力学中起到了举足轻重的作用.关于声子应力、相位子应力、流体声子速度对Re，U和a的响应这里就不一一列举了，以此类推，不难验证结果是相似的.