拖拉机前轮前束值模型建立与仿真
2018-08-15刘晓萌郑小钢
刘晓萌 郑小钢
前轮前束是前轮定位的一种,是为了保证汽车拖拉机直线行驶的稳定性、操纵轻便性以及减少轮胎和机件的磨损,要求前轮和转向节主销安装在前轴上保持相对位置的安装。前轮前束值的不当选择不仅会造成轮胎严重磨损,也会增加驾驶员的操作难度,不利于拖拉机的稳定作业。该文考虑通过调整前轮前束值改变转向力矩的大小,研究了不同车速下轮式拖拉机的转向力矩与前轮前束值的关系。
1 拖拉机前轮转向力学模型的建立
1.1 拖拉机行驶过程中转向的参数模型
拖拉机系统复杂,本文在以下假定条件下分析:路面平整,无空气阻力及风力影响,匀速行驶;前轮转向且转弯半径最小;忽略干涉转向和车身的俯仰及垂直的运动。
拖拉机行驶中转向时驾驶员施加于转向盘的力矩为:

式中:Mz——法向力引起的回正力矩,N·m;
Mf——滚动阻力绕主销产生的转向力矩,N·m;
My——侧向力引起的转向力矩,N·m;
MG——机体抬高产生的回正力矩,N·m。
法向力引起的回正力矩为:
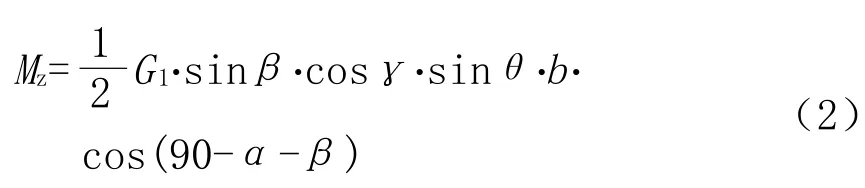
式中:G1——前桥重力,N;
β——主销内倾角,°;
γ——主销后倾角,°;
θ——转向轮转过角度,°;
b——轮胎中心至主销中心的距离,m;
α——前轮外倾角,°。
滚动阻力绕主销产生的转向力矩为:

式中:f——车轮与地面的滚动阻力系数,沥青路面下f = 0.02;
c——主销偏距,m。
侧向力引起的转向力矩为:
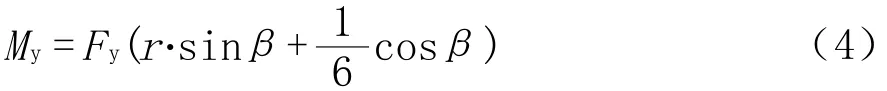
式中:Fy——侧向力,N;
r——前轮半径,m。
侧向力为:

式中:g——重力加速度,m/s2;
v——拖拉机行驶速度,m/s;
R——拖拉机最小转弯半径,m。
机体抬高产生的回正力矩为:
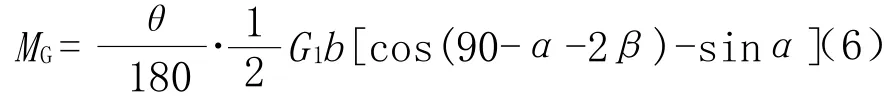

式中:l1——前轴至拖拉机重心距离,m;
m ——整车质量,kg。
前轮前束与前轮外倾的合理配合为:

式中:d——测量前束值对应位置的轮辋直径,m;
L——车辆轴距,m;
l——轮胎接地印迹长度,m。
1.2 拖拉机原地转向的参数模型
原地转向时的转向力矩通常用经验公式进行计算:

式中:μ——静摩擦系数;
p——车轮气压,kPa。
2 某型拖拉机前轮前束参数化模型与实验分析
2.1 参数化模型分析
某型拖拉机的参数值见表1。
将表1中的参数值代入推导的数学模型中,得到转向力矩、前束值和速度三者之间的变化模型,如图1所示。

图1中,速度变化范围为0~15 km/h,前束值变化范围为0~50 mm。从图1可以看出,随着速度和前束值的变化,转向力矩在10~40 N·m范围内变化。

表1 某型拖拉机参数值
2.2 某型拖拉机实车转向力测定
调整该拖拉机前轮前束值为0、17 mm、27 mm、40 mm,用转向力测力仪测出每个特定前束值下车速为0、5 km/h、10 km/h、15 km/h时转向力的大小,并记录数据,建立前束值、车速、转向力矩的关系曲线,如图2、图3所示。
2.3 结果分析
(1)从图1、图2和图3可以看出,在转弯半径最小的情况下,速度保持不变,前束值越大转向力矩越大。前束值一定时,速度为6 km/h时转向力矩较小。
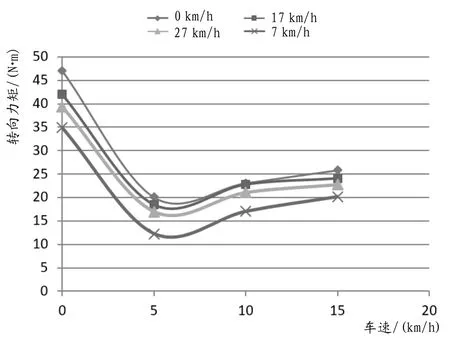
图3 转向力矩随车速的变化曲线
(2)理论分析得到的三维图与依据实验数据绘制的三维图存在一定偏差,但趋势大体一致,说明推导的数学模型具有一定可靠性。
3 结论
该文建立了拖拉机转向力矩、前轮前束值和车速之间关系的数学模型,并通过实验验证了该数学模型的可靠性,可以实现汽车拖拉机采用液压技术在不同工况下自动调节前束值使转向力矩达到最小,同时为汽车拖拉机在无人驾驶或者自动驾驶时实现底盘的自动控制提供了理论依据。
