网络购物购买意愿的影响因素及其复杂关系研究——基于PLS-SEM与贝叶斯网络

李 哲，马中东

(1．大连理工大学 管理与经济学部，辽宁 大连 116024;2．聊城大学 商学院，山东 聊城 252059)

一、引 言

目前，电子商务正凭借着高效便捷的优势全面变革着社会商业模式，网络消费已成为市民热衷的消费方式［1－2］。根据中国电子商务研究中心的调查，2015年、2016年网购市场交易规模高达3．88万亿元和4．7万亿元，分别占社会消费品零售总额的12．9% 和 23．3% 。

网络购物与传统购物相比优势明显，但当前中国的在线消费仍处于起步阶段，在迅速发展的同时也存在不足之处:如网络购物环境有待提高、网络购物市场运行模式有待创新、快递物流方面法律法规相对滞后、消费者维权困难、交易存在不确定性、信息不对称，等等。上述问题在一定程度上影响了网络购物交易成本［3］，而交易成本又影响消费者购买意愿，这是消费者选择网上购物还是传统购物的关键参考。因此，降低交易成本和提升消费者购买意愿是国内外学者和电商企业所关注的焦点。

早期的研究以理论分析为主，如 Bharadwaj和Bigelow等基于交易成本视角，定性对比分析了网络零 售 业 与 传 统 购 物 业 的 交 易 成 本 差 异［4－5］;Rabinovich等基于交易成本视角，对网络消费者的消费行为假设进行了研究［6］。在定性研究的基础上，有学者尝试用统计方法和模型定量研究网络交易成本与购买意愿的关系，如相关分析和回归分析等，但上述方法不能很好地解释变量之间关系且无法解决潜变量测量误差的问题。随着统计学理论的发展，更为严格的统计技术和模型分析方法被引入到网络零售业影响因素的实证研究中，如赵卫宏以网络零售消费者为对象，对网络顾客关系价值及其行为结果进行了实证分析［7］;黄岚等实证分析了网络零售价格促销方式、折扣幅度对网络消费者购买意愿的影响机制［8］，上述研究多是围绕结构方程模型(Structural Equation Model，SEM)技术而开展的。SEM是一种建立、估计和检验因果关系的模型方法，可根据理论模型与样本数据的一致性程度对模型的拟合性做出评价，从而证实所假设理论模型的真伪［9］，但SEM是以观测变量服从正态分布为前提，模型求解严格依赖协方差矩阵，而实际中测量数据的质量受到量表质量、被调查人员主观意识等因素影响，容易出现多重共线性及非正态分布因素造成的偏差问题［10］，从而极大限制了该方法在网络消费者行为研究方面的应用;同时，SEM是基于截面样本点数据的静态估计，主要模拟变量的线性关系，对非线性问题因难以提出严谨的科学假设或有待检验的理论模型，从而无法获得准确的实证结果。偏最小二乘算法(Partial Least Squares Method，PLS)是由Herman Wold提出的一种多因变量对多自变量的多元分析方法，可较好解决普通多元统计分析方法对数据的约束性，如变量X和Y的最大数大于预测方程个数，变量的因子(成分)均从X'X和Y'Y矩阵中提取，但该因子(成分)无法表征变量的相关性;PLS采用对变量X和Y进行分解的方式，从变量X和Y中同时提取成分(因子)，再将成分按照二者之间的相关性从大到小排列，可解决主成分分析提取相关信息时容易漏掉相关性较小的变量而使模型可靠性下降的不足。因此，PLS是将主成分分析与多元回归结合起来的迭代估计，在求解过程中允许测量变量、潜变量为非正态分布［11］，特别适合对数据难以获得且评价体系内具体作用关系不太明确的对象进行探索性研究。构建基于最小二乘法的结构方程模型(简称PLS-SEM)，虽然既能解决测量误差问题又能解决变量非正态问题，并提升了模型实证能力及泛性，但PLS-SEM模型对变量间关系的预测和诊断能力依旧较差。而贝叶斯网络(Bayesian Network，BN)特别适合对变量关系的预测、诊断以及对非线性关系的处理［12］，但其又缺乏对变量间因果关系的解释和实证能力［13］。基于此，本文提出将PLSSEM与BN相结合，该组合模型既发挥了PLS-SEM拟合非标准模型的能力，又发挥了BN的诊断和预测能力，可为电商企业制定合理的价格战略提供智力支持。

二、混合模型基础理论

(一)PLS-SEM的基础

PLS-SEM是伍德(Wold)等于19世纪80年代在PLS回归的基础上提出的一种新型方法，由描述外生潜变量和内生潜变量之间关系的结构方程与描述内、外生潜变量和观测变量关系的测量方程组成。

1．结构模型。结构模型描述的是潜变量之间关系:

其中 η、β、ξ、ζ∈ Rn，Γ ∈ Rn×n;η 是由 m 个内生潜变量(因子)组成的m×1向量;ξ是由n个外生潜变量(因子)组成的n×1向量;Γ为m×n结构系数矩阵，描述了结构模型中外生潜变量ξ对内生潜变量η的影响;ζ是结构模型的m×1残差向量。

由于PLS表示递归关系，因此:

其中βji和γjb为连接预测内生变量与外生潜变量的系数，ζj为内生残差变量。

2．测量模型。测量模型描述的是观测变量与其潜变量之间的关系:

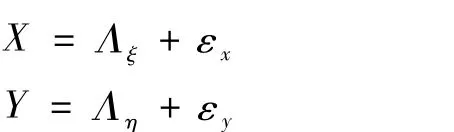
其中x、y分别表示外生与内生潜变量ξ、η的观测变量，Λη是X在ξ上的q×n路径系数矩阵，Λξ是Y在η上的p×m因子负荷矩阵(路径系数矩阵)，权重关系为:

其中 ωlh、ωik分别为用于估计潜在变量 ξl、ηi的第h、k个权重。

SEM的PLS分析方法就是通过迭代每个潜变量的样本估计值^ξl和^ηi，具体计算步骤如下:

步骤1:给定一个任意的初始权重，例如 ωlh=1，其余变量的权重均为0。

步骤 2:按照鲜思东等的方法［14］，计算 ωlh和ωik的新权重值。

步骤 3:判断是否满足|ω'－ω''|＜10－5，成立则进入步骤4，否则返回步骤1，重新赋值。

步骤4:通过公式计算潜在变量 ξl和 ηi的估计值，记为^ξl和^ηi。

步骤5:利用^ξl和^ηi替代ξl和ηi后，运用PLS方法估计结构模型中变量参数。

(二)BN的基本原理

BN是描述数据变量之间依赖关系的图形模型，其基本原理如下:

假设一个有限的离散型由随机变量Xi组成的集合是 U={X1，X2，…，Xn}，其中 Xi可以选取有限个值。一般来说，贝叶斯网络是一个二元组B=〈G，Θ〉:G刻画的是一个有向无环图，其中i个节点与Xi一一对应;Θ刻画的是网络局部条件概率的参数集合{θxi|zi}，θxi|zi=P(xi|zi)，表示节点 Xi对应的每一个值xi在其父节点集yi处于某个特定的配置zi下的条件概率。由B所刻画在集合U上的联合概率分布能够利用式(3)唯一确定，即:

BN的构造可分三步进行，计算过程中并非需要严格按照以下三个步骤进行，可根据实际需求交叉进行。

步骤1:确定变量。

步骤2:构建一个条件独立的有向无环图，由概率乘法公式可得:

若用Yi表示变量Xi的父节点集，可得P(X1，X2，…，

为了确定BN的结构，需将变量X1，X2，…，Xn按某种规则进行排序，以确定能够满足式(4)的变量集 Yi(i=1，2，…，n)。

步骤3:指派局部概率分布P(Xi|Yi)。

(三)组合模型构建步骤

BN模型是对观测变量进行的因果预测与推断，而PLS-SEM是对潜变量层路径关系进行实证分析。因此，融合PLS-SEM和BN模型的关键是通过观测变量获得贝叶斯网络模型推导和预测所需要的样本数据，从而推导出网络消费者购买意愿影响因素的作用机理。鉴于此，本文构建组合模型的思路是:

步骤1:按照PLS-SEM基础中构建PLS-SEM模型的5个步骤，构建网络消费者购买意愿影响因素的PLS-SEM模型。

其中N表示样本量，xi表示第i个观测变量，θδ表示残差的协方差矩阵，T表示矩阵的转置，Φ表示ζ的协方差矩阵。

由式(5)式(6)可知，一旦确定系数Λξ，就可以求得外生潜变量ξ的得分;同理，确定Λη，就可获得内生潜变量η的得分。

步骤3:以PLS-SEM模型实证确定的潜变量间的路径关系作为BN模型的机结，在步骤2的基础上以潜变量的得分作为样本数据，借助 Netica5．19软件，按照BN基本原理中的3个步骤构建潜变量贝叶斯网络模型。

步骤4:在步骤3的基础上，进行购买意愿与其影响因素的贝叶斯推理和诊断。

三、购买意愿及其影响因素的PLS-SEM模型

(一)概念模型的构建

目前，虽然电子商务已获得较快的发展，但无论是发展中国家(如中国等)还是发达国家(如美国等)，传统商业收入远远超过电子商务的收入，造成这种现象的一个重要原因就是消费者对网络购物缺乏信任。Jones等人认为，扩大电子商务市场占有份额的一个关键因素是建立交易双方彼此之间的信任关系［16］;不少文献认为，交易双方彼此之间的信任关系有助于顾客网络消费购买意愿的提升，消费者网络购物市场调查表明，信任度的重要程度高于特定资产。鉴于此，本文将网络购物中的影响因素特定资产换成交易双方的信任度，以探索交易成本对购买意愿的影响。电子商务发展的另一个障碍是网络购物存在多种不确定性，而这些不确定性又提高了线上商业的交易成本。Parkeh研究表明，电子商务在交易过程中具有不确定因素，这类不确定因素阻碍了电子商务的发展，故在研究电子商务交易成本对顾客购买意愿影响时，将不确定性因素作为一个维度保留在交易成本中［17］。因此，本文以交易费用理论(TCE)为理论基础，在文献总结、专家访谈以及QFD专家头脑风暴法的基础上，将网络购物交易成本分为不确定性、购买频率、信任度三个维度，并探索其对消费者购买意愿的影响。

根据以上分析，网络消费中交易成本与购买意愿关系的概念模型，见图1。

图1 交易成本与购买意愿关系概念模型图

图1所示概念模型的路径假设有:

H1:交易成本与购买意愿是负相关的关系，交易成本可对购买意愿进行逆向调节。

H2:不确定性与购买意愿是负相关的关系，不确定性可对购买意愿进行逆向调节。

H3:交易频率与购买意愿是正相关的关系，交易频率可对购买意愿进行正向调节。

H4:不确定性与交易成本是正相关的关系，不确定性可对交易成本进行正向调节。

H5:交易频率与交易成本是负相关的关系，交易频率可对交易成本进行逆向调节。

H6:交易频率与不确定性是负相关的关系，交易频率可对不确定性进行逆向调节。

H7:信任度与购买意愿是正相关的关系，信任度可对购买意愿进行正向调节。

H8:信任度与不确定性是负相关的关系，信任度可对不确定性进行逆向调节。

H9:信任度与购买频率是正相关的关系，信任度可对购买频率进行正向调节。

H10:信任度与交易成本是负相关的关系，信任度可对交易成本进行逆向调节。

(二)模型的实证与分析

为了验证概念模型的正确性，需要对模型效度、拟合优度检验以及模型参数进行估计。结合文献调研和实际需要，本文设计的量表共有五个潜变量:交易成本、不确定性、购买频率、购买意愿、信任度(见表1)。量表采用的是Liket五分量表，将选项分为“非常同意”、“同意”、“不一定”、“不同意”、“非常不同意”，每个回答对应的得分分别是 5、4、3、2、1，认同程度越高，分数越高。本文采用非概率抽样方式进行，调查对象选择网民中所占比重较大的在校大学生、企业白领和教师。

表1 网络消费者购买意愿及其影响因素调查表

本次调研共计发放问卷708份，有效问卷(不缺失、不雷同)636份，有效率为88．3%。对有效问卷的数据进行数据质量检验，其检验显示五个潜变量的Cronbach's Alpha均在0．75以上，即表明样本数据具有很好的信度。为了验证样本数据的效度，对样本数据进行 KMO测量和 Bartelett球形检验，结果显示KMO 值为 0．81 ＞0．80、df=120、p=0，即表明数据适合做因子分析［18］。借助SPSS20软件，进行因子分析可知，观测变量因子载荷系数均大于0．5，观测变量能够有效地体现潜变量，切合本文的研究要求。

1．PLS-SEM模型的效度检验、拟合度检验

(1)PLS-SEM模型的效度检验。测量模型的评价是借助潜变量预测显变量的blindfolding公因子方差测度完成的，而结构模型的评价是运用blindfolding冗余测度实现的，其中测量模型的检验结果如表2所示，结构模型的检验结果如表3所示。

表2 测量模型效度检验结果表

表3 结构模型效度检验结果表

(2)PLS-SEM模型的拟合分析。为使PLS-SEM的正确合理性得到验证，需要对一系列的拟合指数是否达到参考值进行评价，若指标均满足则拟合效果较好，反之不好，模型拟合结果见表4所示。

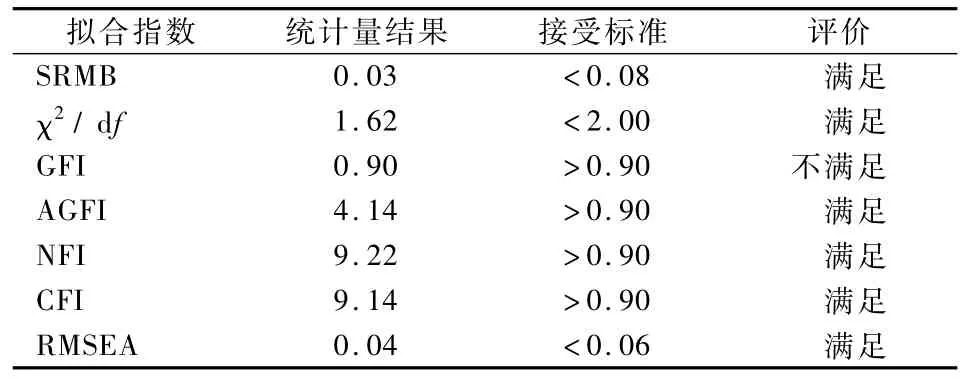
表4 PLS-SEM的主要拟合效果指数表

从表4可知，PLS-SEM的拟合指数除GFI外，其他均达到接受标准，虽然模型的拟合指数GFI没有达到参考值，但与其接受标准相差不大，因此可认为其达到接受标准，不需要重新调整，即说明该模型的整体拟合程度较好。

2．PLS-SEM模型的参数检验

在PLS-SEM模型效度、拟合度检验的基础上，首先赋予显变量相同权重，并以此赋值显变量所在的潜变量;再在此基础上获得表示显变量与潜变量相关性的回归系数，即因子载荷系数和表示潜变量之间相关性的回归系数，即路径系数;然后在代理回归原则的指导下，递归迭代15次，直到路径系数迭代收敛。图2显示了最终的PLS-SEM结构，该模型表明了显变量对潜变量和潜变量对潜变量的路径系数。

图2 交易成本对购买意愿的路径系数分析图

四、购买意愿影响因素的BN模型

(一)BN模型的构建

网络结构中的五个变量均为潜变量，本文利用SmartPLS 3．0计算网络结构中五个潜变量的得分。在此基础上，以潜变量的得分为样本数据，利用K-means聚类分析方法对样本数据进行聚类。同时，为了降低运算的复杂性和增加判断结果的可识别性，本文将每个潜变量都聚类为高、中、低三种状态，然后计算获得每个潜变量的先验概率，见表5所示。

表5 各潜变量的先验概率表

在已知五个潜变量先验概率的条件下，利用Netica5．19软件确定某一潜变量发生条件下的其他潜变量发生的概率，即条件概率，见表6(a)～6(c)。

表6 (a) 信任度发生条件下的条件概率表

表6 (b) 购买频率发生条件下的条件概率表

表6 (c) 不确定性发生条件下的条件概率表

(二)贝叶斯推理

运用已创建的贝叶斯网络，在已经获得潜变量的先验概率前提下，可以对其他潜变量进行贝叶斯推理以获得其条件概率(后验概率)。例如，假设消费者的信任度很高(交易成本“高”的概率设为1．00)，运用BN推理、预测能力，则可得到购买意愿“高”的概率为0．623。表7显示的是在不同信任度状态下对购买频率、不确定性、交易成本和购买意愿的预测。

表7 信任度在不同状态下的贝叶斯推理表

如表7所示，随着信任度“高→中→低”的变化，不确定性和交易成本与之成反向变化，购买意愿和购买频率与之成正向变化，其中不确定性和交易成本“高”的概率具有显著递增的规律，而购买频率、购买意愿“高”的概率具有明显递减的规律;购买频率和购买意愿“中”的概率呈现先递增后递减的规律，而不确定性与交易成本“中”的概率呈现先递减后递增的规律;购买频率和购买意愿“低”的概率出现显著递增的规律，而不确定性和交易成本“低”的概率出现显著递减的趋势规律。从表7可以推断出信任度对购买意愿的影响最大，即当信任度由高到低变化时，购买意愿变化的幅度最大;表8为购买频率在不同状态下对不确定性、交易成本和购买意愿的预测;表9为不确定性在不同状态下对交易成本和购买意愿的预测(见表8表9)。

表8 购买频率在不同状态下的贝叶斯推理表

表9 不确定性在不同状态下的贝叶斯推理表

(三)贝叶斯诊断

贝叶斯网络具有较强的因果推断能力，包括贝叶斯推理与诊断。贝叶斯诊断是贝叶斯推理的反向运算，即贝叶斯网络由果索因，通过因变量的状态获知自变量的能力。例如，假定不确定性是高的(BN中将不确定性“高”定为1．00)，运用贝叶斯逆向诊断的能力能够得到信任度“高”的概率为0．226。表10显示的是在购买意愿的基础上，对购买频率、不确定性、交易成本和信任度做出的贝叶斯诊断。

如表10所示，随着购买意愿发生“高→中→低”的变化，购买频率和信任度“高”的概率出现显著的递减规律，而不确定性和交易成本“高”的概率出现显著递增规律;购买频率和信任度“中”的概率出现先上升后下降先增后减的趋势，“低”的概率出现递增的规律;而不确定性和交易成本中“中”的概率出现先减后增的趋势，“低”的概率出现递减的趋势规律;购买意愿状态明确的情况下，可以知道交易成本发生并对其产生影响的概率最大。例如，当购买意愿高时交易成本低的发生概率为0．657;当购买意愿低时交易成本高的概率为0．651。由表10还可知，当企业将交易成本控制在很好的状态时，比较容易促进消费者形成高的购买意愿，企业可以根据购买意愿发生的变化，有目的地去调节交易成本、不确定性、购买频率和信任度，以此促进购买意愿的提升。此外，还可依据BN获得交易成本、不确定性与购买频率的状态，为交易成本降低、购买意愿的提升提供决策依据。表11(a)、表11(b)、表11(c)分别是交易成本在不同状态下的贝叶斯诊断、不确定性在不同状态下的贝叶斯诊断、购买频率在不同状态下的贝叶斯诊断。

表10 购买意愿在不同状态下的贝叶斯诊断表

表11 (a) 交易成本在不同状态下的贝叶斯诊断表

表11 (b) 不确定性在不同状态下的贝叶斯诊断表

表11 (c) 购买频率在不同状态下的贝叶斯诊断表

五、结 论

了解网络购物消费者购买意愿与交易成本的关系和获得降低交易成本、提高顾客满意度的方法，是各国学者及电商企业关注的焦点。当前，关于交易成本与购买意愿关系的研究相对不多，其研究以结构方程模型为主，未能很好地处理变量之间的非正态、非线性关系，且预测精度较低。为了解决以上问题，本文提出了PLS-SEM与BN的组合模型，该组合模型可更加清晰地为电商企业价格战略提供指导。

本文主要结论如下:

第一，交易成本与购买意愿是负相关的关系，交易成本可对购买意愿进行逆向调节，监督成本和搜寻成本是交易成本六个观测变量中对交易成本影响最大的两个变量;信任度、购买频率和不确定性既是影响交易成本的潜变量，也是影响购买意愿的潜变量，其中信任度对交易成本的影响最大、其次是不确定性、最后是交易频率，而这三个潜变量中Unc1(行为不确定性)、Unc5(声誉不确定性)对不确定性的影响最大，PF3(网购倾向性)对购买频率影响最大，Con2(网购值得信赖)、Con5(卖家声誉是好的)对信任度影响最大。

第二，交易成本与购买意愿之间的关系可以应用贝叶斯网络正向推理、逆向诊断的能力进行研究。通过贝叶斯推理可知:交易成本在高、中、低不同状态下购买意愿发生的概率;交易成本的父节点在不同状态下交易成本发生的概率，也可以通过贝叶斯诊断获得在子节点状态确定的情况下其父节点的状态，进而为管理决策提供支持。