BP-ANN预测网络关系中的数据降维与模型综合方法

马 峻，万 劼

（首都经济贸易大学 安全与环境工程学院，北京 100070）

0 引言

复杂网络广泛存在于社会各个领域。社交网站用户构成的社交网络，反映的是社交网站用户之间的好友关系或关注(收听)关系；商店顾客与商品构成的购买关系网络，反映的是顾客对商品的购买关系；其他诸如航空网络、国家的电力网络、蛋白质相互作用网络、食物链网络等。不论是什么种类的网络，一个网络可抽象为由点集P和边集E组成的图G=(P,E)，设R是从P到其自身的一个二元关系，即R⊂P×P，对任意(x,y)∈P×P，如果xRy，则从x有一条有向连边指向y，连边反映了x与y的一种二元关系，如果(x,y)≠(y,x)，则构成一个不对称关系，否则为对称关系。但在数量方面，同样规模的网络中，二元不对称关系的潜在数量往往比二元对称关系多；在信息量方面，二元不对称关系更具有方向性，因此描述二元不对称关系的网络要比描述二元对称关系的网络包含更多的信息量。网络中存在的这种关系对于网络影响力的拓展以及网络资源的有效利用具有很大的价值[1]，二元不对称关系相对于二元关系的研究更具有普遍性和研究意义。

目前针对社会网络中的二元关系的预测主要基于的信息可分为三类，第一类是根据网络节点属性信息进行预测；第二类是根据网络结构信息进行预测；第三类是上述两类的混合方法，即在预测中既使用节点属性信息也使用网络结构信息。文献[2，3]表明使用节点属性信息对社会网络中的二元关系进行预测求解可以得到较好的效果，但是使用节点属性信息存在着以下问题：第一，大量的节点属性信息很难获取，可靠性也难以得到保证；第二，需要大量的资源来存储、读取节点属性信息。但是根据网络结构信息进行关系预测求解一般不存在上述两个问题。

根据网络结构信息进行关系预测求解中，一类是基于节点相似度的关系预测求解方法，另一类是基于似然分析的预测求解方法。基于相似度的关系预测求解方法较为简便，需要的假设前提较少，而基于似然分析的关系预测求解方法较为复杂，且需要建立在较多的假设(如层次结构、社团结构等)之上，使用较少。文献[4]将节点相似度与机器学习方法相结合，收到了较好的求解效果，但是还存在一些有待解决的问题；其次，基于节点相似性的关系预测方法在处理二部分网络时会遇到困难，例如很多常用的相似度指标是无法计算的，这时一般需要使用一些更为复杂的相似度指标，或者采用集合投影和协同过滤的方法[5-7]，这些方法或是较为复杂，或是有待完善。而神经网络(Artificial Neural Network，ANN)作为一种非线性动力学模型广泛用在各个领域预测求解，但是神经网络在进行社会网络关系预测计算中，由于社会网络的动态性和时变性导致网络资源拓展的不确定性，同时社会网络规模大、小世界性小社团等特性导致网络邻接关系矩阵稀疏和不均匀性，产生社会网络预测求解中输入数据维数高，同时网络中存在的不平衡性也极大地影响了神经网络预测计算的效果[8]，为此，本文针对这两个问题，在提出相应降维算法基础上，建立了如何克服不平衡性从而提高模型求解效果的方法。

1 问题描述

本文采用BP神经网络对社会网络二元不对称关系进行预测求解的基本逻辑过程如下页图1所示。

图1 利用BP神经网络进行社会网络二元不对称关系预测求解逻辑过程

T=(SR)反映训练集所有样本在整个网络的连接关系。

P=(UV)反映了预测求解集所有样本在整个网络的连接关系。

S和U分别是训练和预测求解的输入值，R是训练输出值，V是预测求解输出值。S，U，R是邻接矩阵的已知部分，V是邻接矩阵的未知部分。

实际应用中V的某些部分可能是已知的，但鉴于一般V占整个邻接矩阵的比例较小（不大于1/9），而考虑V的已知部分会增大算法和代码的复杂度，因此将V的全部设为未知。如果只需要预测求解V的部分列向量，那么就不需要获取关于R的全部信息，只需要知道R所对应列向量的取值。

根据图1，预测求解需要大量的训练样本，因此An×n的m会很大，如果将S和U这种高维向量直接作为输入，则算法复杂度会很大，因此需要采取适当方法进行降维；另外由于网络中大部分节点对是不存在关系的（这种情形也被称为数据不平衡），而神经网络算法通常以训练误差最小化为目标求解模型，这会导致模型倾向做出关系不存在的预测，而实际应用中更多被关注的是存在的关系，将存在的关系判断为不存在所导致的损失经常远大于将不存在的关系判断为存在所导致的损失，因此需要对模型进行进一步的处理。

2 数据降维

2.1 数据降维方法

根据图1，在利用神经网络进行关系预测时，需要将关系矩阵An×n中Sm×m的m个变量取值全部直接输入到神经网络输入层，通常较大的m将导致神经网络规模也会变大，将大大增加算法的复杂度，因此有必要设法减少输入层的节点数。

根据邻接关系矩阵An×n，m个原始输入变量的取值只有0与1两种可能，又因为这个变量的顺序是固定不变的，因此神经网络输入层其实是一个长度为m的0-1向量，为此可以将其固定长度转化为一个整数，从而实现数据的降维。具体方法如下：

设πn为全体n维0-1向量构成的集合，Z为整数集。对∀x∈πn，x可被表述为如下形式：

再做如下映射：

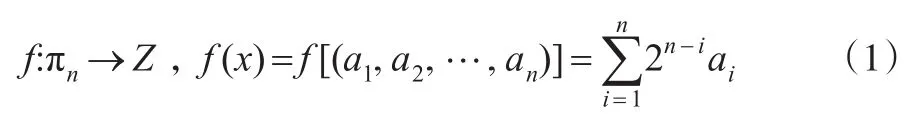
对于f，有如下命题成立：

命 题 1：对 ∀x1,x2∈πn，若x1≠x2，则 必 有f(x1)≠f(x2)。

采用反证法可以对上述命题进行证明。

命题1说明：f可将不同长度的0-1向量转化为不同整数，并且通过fn进行数据降维的过程中不会丢失原有的任何信息。

2.2 存在的问题

理论上任意n维0-1向量可以转化为一维整数，因此可以将m个输入变量转化为一个输入变量，这样神经网络的输入层节点数最少只需要一个，而不是m个。但是，如果仅仅用一个十进制数替代原先的m个变量，那么可能会大大增加神经网络的训练难度。

例如：设m为5，样本A的原始输入向量为(1，0，0，0，1)，转化为十进制数，即为17。样本B的原始输入向量为(0，0，0，0，1)，转化为十进制数，即为1。A和B只在一个位置上不同，应该说两个样本比较相似。但是转化为十进制数后，两个样本对应的输入值要相差16倍。再设样本C的输入向量为(0，1，1，1，0)。C与A在所有位置上都不同，但是C的输入向量转化为十进制后为14，反而与A比较接近。一般来说，A与B的输出值往往是相同的，而A与C的输出值更可能是不同的。这意味着输出值对输入值的变化非常敏感，而且通过神经网络得出的预测函数会有高频且大幅的波动。

虽然神经网络算法比很多其他算法更善于处理此类非线性的回归，但在输入值与输出值之间几乎毫无线性相关性的情况下，如果训练样本并不是很多，那么神经网络也较难做出准确的预测。

2.3 分段降维算法

解决上述问题的办法是将原始m维输入向量分为k段（k＞1），提高算法效率同时保证算法的有效性。m维的输入向量分为k段，每段转化为一个整数，输入变量转化为k个整数。这样对于任意一个样本集，设原始输入向量x=(a1,a2,…,am)（ai∈{0,1}，i=1,2,…,m），分段降维结果y=(b1,b2,…,bk)∈Zk（k≤m）。

k的取值既不能太大，也不能太小。如果k太大，达不到降低神经网络输入层维数的目的，如果k太小，则输出值对输入值的变化会很敏感，从而增加神经网络学习的难度。由于k实际上就是输入层的节点数，因此k是一个影响神经网络结构的变量，而神经网络结构也会影响预测的效果。

分段降维算法如下：

步骤1：ifk|m!=int

步骤1.1：设h=m'/(k-1)

步骤1.2：Forj=0tok-2

依次将 (ajh+1,ajh+2,…ajh+h)记为Aj+1,将x的最后(m-m')个分量(am'+1,am'+2,…,am)记为Ak

步骤2：ifk|m=int

步骤2.1：设h=m/k

步骤2.2：Forj=0tok-1

依次将 (ajh+1,ajh+2,…ajh+h)记为Aj+1,将x的最后(m-m')个分量(am'+1,am'+2,…,am)记为Ak

步骤3：得到分为k段的向量x，记为(A1,A2,…,Ak)

步骤4：Forj=0tok

∀Aj∈{A1,A2,…,Ak}将Aj转化为整数f(Aj)

bj=f(Aj)

步骤5：得到k维整数向量y=(b1,b2,…,bk)∈Zk

上述将An×n划分为An×n的过程中，可以保证An×n都有相同的维数An×n，并且能使An×n尽量大。这样，An×n就能较为“均匀”地被划分为An×n段。同时由于分段降维算法对于每个二进制数都会与一个十进制数一一对应，因此降维前后的数据之间存在一一映射，降维并没有使数据所包含的信息量减少，整个数据降维过程是可逆的。

3 模型综合法

数据的降维提高了神经网络计算的效率，但是由于复杂社会网络存在关系的复杂性，以及所拥有的幂律特性导致在利用神经网络进行关系预测时存在的不平衡性问题，即对于关系比较密集的社会网络，预测出不存在的关系实际是存在的，反之在稀疏关系网络预测出存在的关系实际是不存在的，这种不平衡性是由于模型本身造成的[8]，为了消除这种不平衡性，本文构建预测模型综合评价指标基本上建立模型综合方法，具体实现过程如下。

3.1 基本评价指标

神经网络预测模型的评价是建立在邻接矩阵An×n基础上，设Y=(aij)(n-m)×q是An×n中V的一个子矩阵，表示V中全部待预测的部分，q是待预测的列向量的数量。X=(bij)(n-m)×q是对Y的预测值（Y为真实值）。||A表示任意有限集合A的基数，N+表示正整数集，则有：

Np=(n-m)q，即Np为Y的元素总数；

Nt=|{(i,j)∈N+×N+|aij=bij}|，即Nt为预测正确的次数；

Mp=|{(i,j)∈N+×N+|aij=1}|，即Mp为预测集中真正存在的连边数量；

Mt=|{(i,j)∈N+×N+|aij=bij=1}|，即Mt为在连边真实存在的条件下，正确预测的次数。

评价指标有两个。一个是总预测准确率P1，另一个是正类预测准确率P2。

从本质看P1反映的是模型整体的预测准确率，P2反映的是模型对关系存在性的发现能力。之所以要进一步计算P2，是因为在分析实际问题中，人们往往更关注关系的存在性，而对关系的不存在性并不那么关注，从广义上来看，关系的存在性与不存在性的受重视程度是不同的，P2会增强模型对非重视关系的发现能力。

因此P1和P2是评价模型预测效果的两个基本指标，两个指标缺一不可。如果忽视P2，而只看P1，那么将正类误判为负类的概率就难以得到控制。另一方面，如果P2很高而P1很低，那么总的误判损失还是会很大。为了弥补这个缺陷，本文建立基于P1和P2基本指标的综合评价指标。

3.2 综合评价指标

将基本指标P1和P2加权平均可以得到一个新的综合指标Pc，Pc可由式（4）确定：

γ1和γ2的取值是与使用者对P1和P2的重视程度有关，但是在实际应用中Pc计算方法未必能真实体现使用者对P1和P2的重视程度。这是因为P1和P2的标准差可能会有很大差异，在许多复杂网络中(尤其是连边较为稀疏网络中)，由于真实存在的连边要比节点对总数少很多，往往P2的标准差要比P1大很多，影响P2的偶然随机因素要比P1大，P1的差异更大程度上是模型本身因素导致的。为了消除上述影响，只有对P1和P2做调整，使两者的标准差相同，才能更加客观地评价模型的预测能力。

设σi是Pi的标准差，则P1σ1和P2σ2具有相同的标准差，带入公式（4）可得到：

其中γi由人为主观决定。σi是Pi总体的性质，无法直接结算，但是可以根据不⁀同模型得到的Pi值，通过计算Pi的样本标准差 ，再将作为σi的估计值。

3.3 模型综合

利用神经网络进行关系预测时，不同的模型参数，相同的输入其输出的预测结果也不同，在这里把拥有不同参数的神经网络预测模型称为不同的分类器。在实际问题求解过程中，如果以预测效果最好的一个分类器预测结果为准，可能会导致较大的误判风险，因为一个分类器预测效果的好坏，通常需要通过已知样本进行检测才能得出，当一个分类器在用于检测模型效果的已知样本上表现出良好效果时，虽然可以认为该分类器的预测能力是较强的，但其未必会在待预测的未知样本上也能取得最好的效果。即使该分类器在未知样本上的预测能力仍然是最强的，其预测效果也未必好于将多个分类器综合得出的结果。因此，相对于仅仅“信任”一个分类器的做法，本文将若干个分类器组合起来进行预测，降低结果的误判风险。基本原理是对各神经网络预测模型赋予权重，根据各个分类器的预测值加权平均来获得最终预测结果，加权平均值表达形式如下：

其中，H为分类器个数，yi是第i个分类器的预测值，βi第i个分类器的权重系数。问题的关键转换为如何得到每个分类器的βi值。

在公式（6）中，βi值的大小是与预测效果成正比的，如果只考虑两个分类器ρ1和ρ2的情形下，分类器ρi（i=1,2）的权重系数βi的计算公式为：

其中，Pc(ρi)是分类器ρi对检测集样本的预测效果综合评价指标Pc的值。在其他条件不变的情况下，βi与Pc(ρi)成正比，说明预测效果越好，权重系数越大。而φ(ρ1,ρ2)是两个分类器ρ1和ρ2预测值相同的概率，，其中Ns是用于检测集样本总数，yρ1,i和yρ2,i分别是分类器ρ1和ρ2对第i个检测集样本的预测值。

根据公式（7），φ(ρ1,ρ2)越大，则βi越小。如果φ(ρ1,ρ2)达到最大值1，则有：

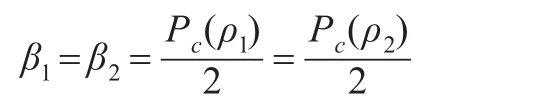
这样，在使用两个预测结果完全相同的分类器的情况下，两个分类器权重系数总和与仅仅保留其中一个分类器的情况下的权重系数是相同的。如果φ(ρ1,ρ2)达到最小值0，则βi=Pc(ρi)，说明当两个预测结果完全不同的分类器组合起来时，他们各自的权重都不会被削弱。

把式（7）式扩展到两个以上分类器的情形，在有H个分类器情况下，第i（i=1,2,…H）个分类器ρi的权重系数βi的计算公式为：

由于φ(ρi,ρi)=1，因此式（8）又能写成以下形式：

因此，模型综合的权值βi求解过程为：

步骤1：从已知样本中抽出一部分，将其作为检测集样本，并用各分类器对检测集样本进行预测，得出预测值；

步骤2：根据第一步的预测结果，计算各分类器的Pc值；

步骤3：计算每两个分类器预测值相同的概率φ(ρi,ρj)；

步骤4：利用式（9）计算βi。

4 实例验证

本文以美国政治博客引用关系网络为实例（数据来源于www.linkprediction.org 2014年6月），网络中节点是博客文章，如果博客文章A引用了博客文章B，则在网络中代表文章A的节点会有一条有向边指向代表文章B的节点。验证数据选用这一网络的一个导出子网络进行实证分析，该子网络包含150个节点，将网络中的节点编号为1～150号，并将这150个节点构成的集合记为Np。以1～100号节点为训练集，101～150号节点为预测集。为检验算法效果，假定有序节点对集合Yp={(x,y)|x∈Np,y∈Np,101≤x≤150,106≤y≤150}中的二元关系存在性是未知的，其余节点对的二元关系存在性是已知的。然后从106～150号节点中随机选择10个节点，构成集合Kt，利用本文提出的方法对有序节点对集合Y={(x,y)|x∈Np,y∈Kt,101≤x≤150}中的二元关系存在性进行预测。

神经网络求解约束条件设置：①训练的最大迭代次数为1000；②连接函数选择为Logistic函数；③初始开始进行训练的次数选为50；④训练的学习率取值为0.01；⑤训练时观察模型误差的频率是每迭代10次观察一次；⑥迭代收敛的判断标准是相邻两次观察到的误差值相差小于5×10-7。

不同分类器的参数调整是：①输入向量的维数k；②隐藏层的节点数s；③正类样本权重c。

将Yt={(x,y)|x∈Np,y∈Np,101≤x≤150,101≤y≤105}作为检测集，以检测不同参数下模型的预测效果。在k取10和20、s取15和30、c取5和6情况下，三个参数的全部组合共是8，分别在这8个参数组合下对检测集进行预测实验。测试实验发现s为30，c为6情况下的两个模型预测效果最好。于是s取为30，c取为6，再分别取k为5、15和25，进行三组实验。

根据算法1，在k取5情况下的数据降维是：

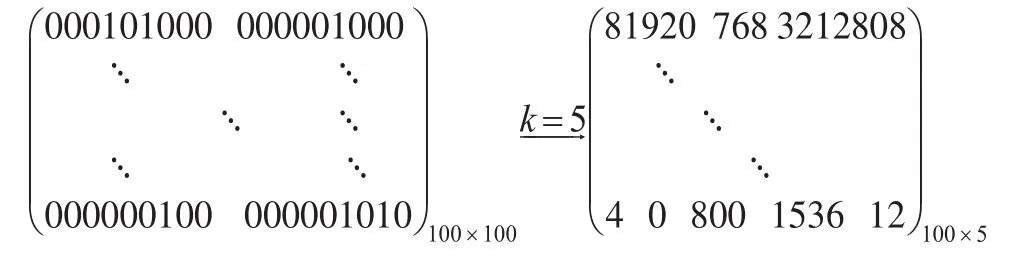
根据公式（2）和（3）计算得到11个参数组合下预测模型评价指标如表1所示。

表1 参数组合及预测模型评价指标

计算出表1中任意两个模型预测值相同的概率如表3所示。

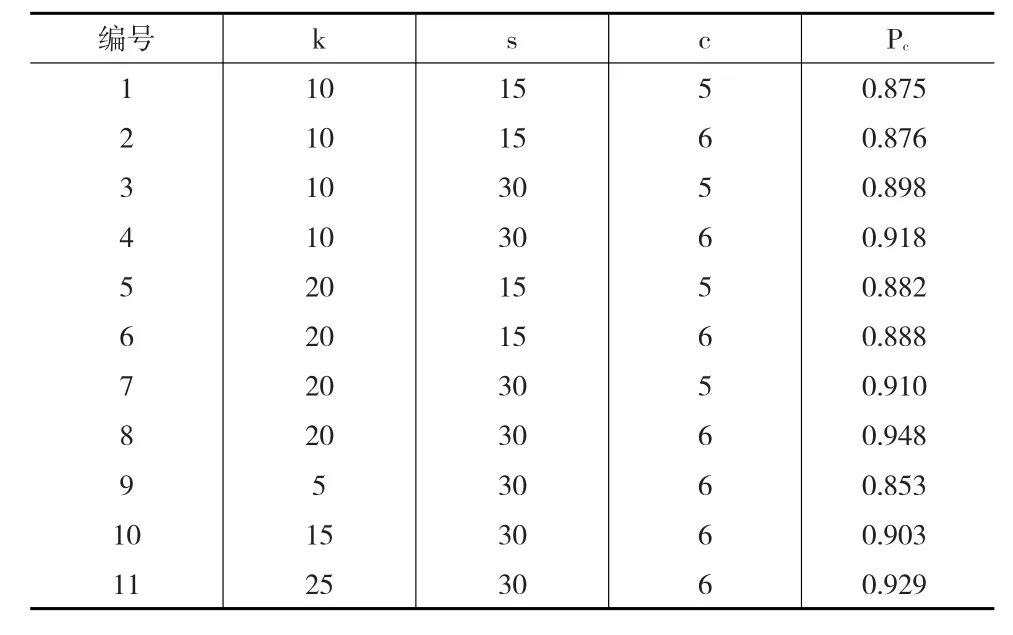
表2 各个预测模型综合评价指标值

表3 任意两个模型预测值相同的概率

根据公式（9）各个模型权重系数βi如表4所示。

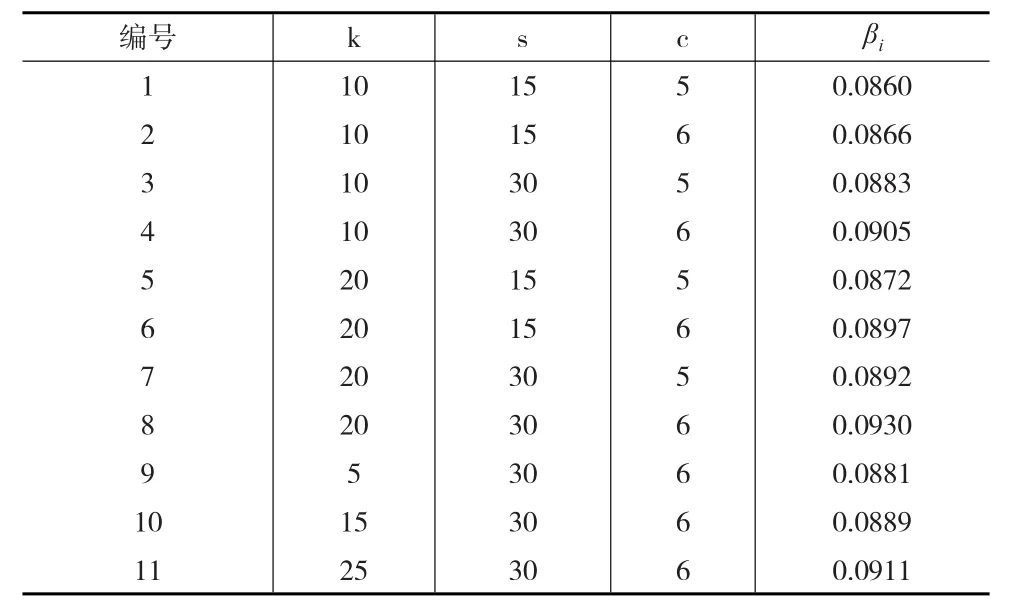
表4 各个模型的权重系数（归一化前）

依据表1中11个模型对Y中的关系进行预测，得出各模型对Y中有序各节点对关系存在性的预测值，然后对于每个待预测的有序节点对，根据式(6)并采用表4的βi值计算各模型预测值的加权平均，该加权平均值即为整个模型最终的预测值。将各模型的预测值以及模型最终预测值与真实值做比较，计算各模型的P1值和P2值以及模型综合的预测效果P1值和P2如下页表5所示。

从表5可以看出，最终对预测值求加权平均后得到的综合模型的P2值是所有模型中最高的。虽然3号模型和8号模型的P2值与最终综合模型的P2值相同，但这两个模型的P1值都相对较低。在P1值方面，除去10号模型与11号模型以外，其他模型的P1值都比最终综合模型低。10号模型与11号模型的P1值比最终综合模型的P1值略高，但在P2值方面却不如最终综合模型。根据表5，可以计算出各模型的Pc值(其中对P1和P2的重视程度相同)如表6所示。

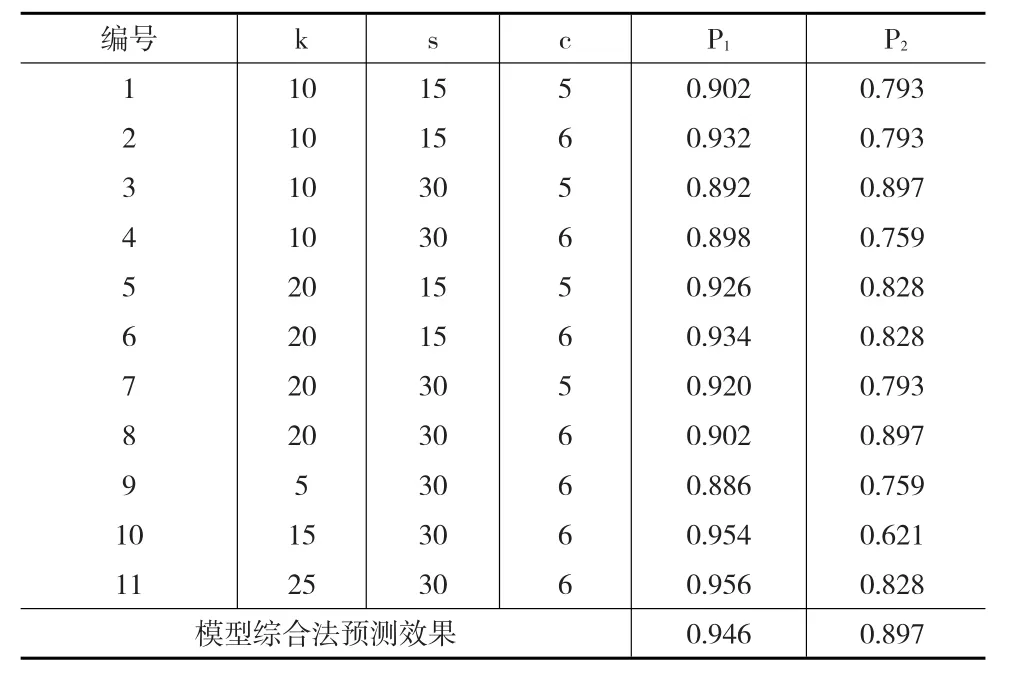
表5 各模型的预测效果以及模型综合法预测效果

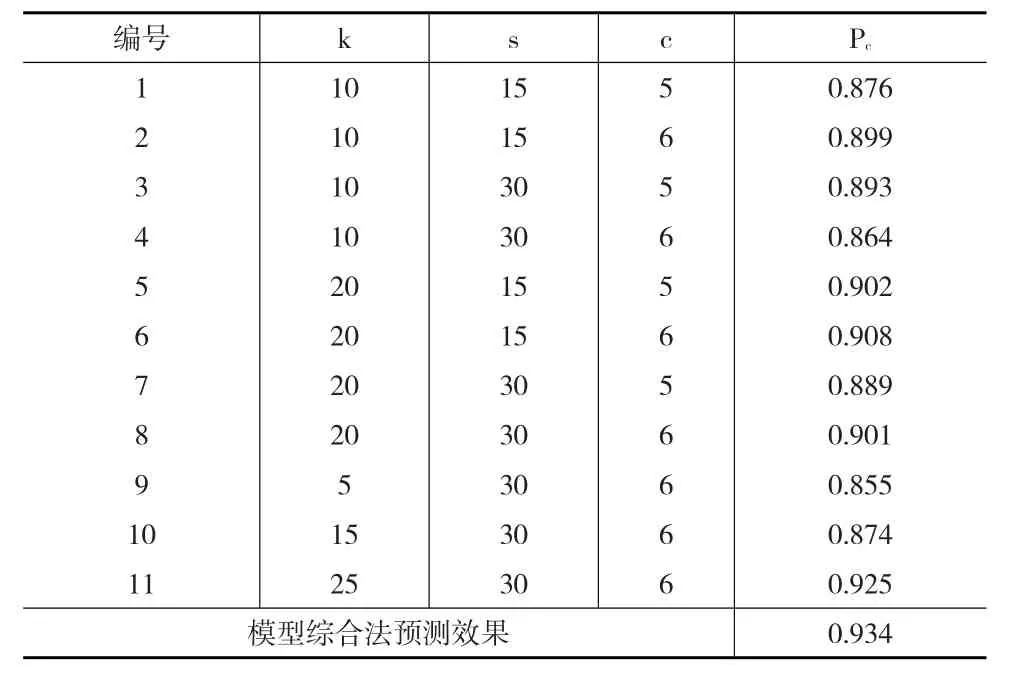
表6 各个模型的预测效果综合评价指标值

从表6可知，在对P1和P2的重视程度相同的前提下，综合模型的Pc值是最高的。可见综合模型预测效果比单个模型要好。

5 结束语

随着互联网+的不断发展，社会网络逐步渗透到社会各个领域，充分利用网络资源拓展服务成为互联网经济时代面临的一个突出问题，而有效地预知网络中二元不对称关系可以为用户准确地把握措施的实施提供了有力的支持。本文基于社会网络的复杂性和动态性，利用神经网络预测特性，构建了预测时高维输入向量降维的算法，在建立模型综合评价指标基础上，构造了具有消除不平衡性的模型综合预测方法，实例验证表明，本文所提算法和方法是有效的。