混频误差修正模型的有效性探讨

孙 毅，秦 梦

（青岛大学 经济学院，山东青岛266071）

0 引言

宏观经济的预测对制定宏观经济政策来说尤为重要，诸多指标可反映宏观经济的运行状况和未来走势，然而这些指标与用于预测这些指标的数据频率往往有所差异，因此在建立传统模型前必须对混频数据进行处理，进而转化为同频数据，但这将造成信息的损失或虚增，不利于模型的预测效果。为克服这一缺陷，Ghysels E等[1]提出MIDAS混频模型，可以将不同频率的数据构建在同一模型中，而不需要对原始数据进行处理。

MIDAS混频模型可充分利用混频数据信息，能够提高预测精度，基于此，学者们对该模型进行了深入研究，MIDAS混频模型也得到进一步发展。Clements M P等[2]提出带有自回归项的MIDAS混频模型，用于解决例如GDP这样存在自相关性的时间序列，并证明其优于同频自回归模型。Foroni C等[3]提出无约束的MIDAS模型，并不是说它一定优于有约束的MIDAS模型，而是两者可以相互补充，针对不同情况选取最优模型。Götz T B等[4]提出的ECM-MIDAS模型和Miller J I[5]提出的CoMIDAS模型，都是对具有协整关系的不平稳的时间序列在构建混频模型时，加入误差修正项，避免不平稳的混频时间序列出现“伪回归”，同时避免对不平稳的时间序列差分后建立混频模型，造成信息损失，以提高模型的预测精度。在本文中，ECM-MIDAS模型和CoMIDAS模型均可称之为混频误差修正模型，但两者的建模方法有所区别。

国内学者基于以上两种混频误差修正模型均有研究，李会会[6]基于ECM-MIDAS模型对通货膨胀率进行预测研究，并得出ECM-MIDAS模型的预测效果优于MIDAS模型和同频模型的结论。刘汉[7]基于M1，运用CoMIDAS模型对GDP进行预测，证明该模型比AR模型的预测更准确，但并未证明其预测效果优于无误差修正项的混频模型。由此可见，这两种混频误差修正模型具有一定的合理性，可以处理非平稳但具有协整关系的混频数据。

然而，国内外学者并没有对上述两种模型的预测效果进行比较，因此，为比较两种混频误差修正模型的有效性，本文首先对两种形式的混频误差修正模型进行推导，而后基于此以M2和GDP作为样本数据构建模型进行实证分析，最后与同频误差修正模型和无误差修正项的同频、混频模型的预测效果相比较，证明了混频误差修正模型的有效性，且在此例中，ECM-MIDAS模型的预测效果要优于CoMIDAS模型，但并非指ECM-MIDAS模型有绝对的优势，在进行实证分析时仍须具体问题具体分析，选择最优模型进行估计和预测，但实际上由于二者预测误差相差不大，模型的选择不会对结果有太大的影响。

1 MIDAS模型简介

根据MIDAS模型是否设定滞后权重多项式，即是否对高频解释变量的滞后多项式参数施加约束条件，可将MIDAS模型分为有约束和无约束两类。

1.1 有约束的MIDAS模型

所谓约束，就是指对高频解释变量的滞后多项式参数施加了某个或某些约束条件，如对滞后多项式设定权重，按照所设定的权重进行线性回归或非线性回归，而后求得其参数。有约束的MIDAS模型可写为如下形式：

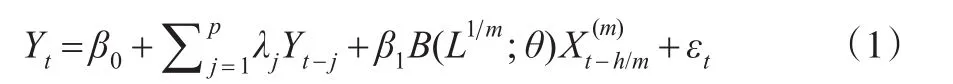
在式（1）中，Yt为被解释变量（即低频数据）；Yt-j为被解释变量的滞后项；p为低频被解释变量的最高滞后阶数；为解释变量（即高频数据）；m表示被解释变量与解释变量之间的频率倍差，在本文中设定为月度数据，Yt为季度数据，则m的值为3；权重函数与滞后算子结合有；滞后算子有，其中k∈[1,K]；K+h-1为高频解释变量的最高滞后阶数（以高频频率计算，下同）；h为向前预测的步数。

若Yt为季度数据序列，为月度数据序列，设Yt为2015年第四季度的数据，那么即为2015年12月的数据，为2015年11月的数据，为2015年10月的数据（也可写为）为2015年9月的数据，以此类推。例如，设K=6，当h=0时（即没有向前预测），MIDAS混频模型可表示为：

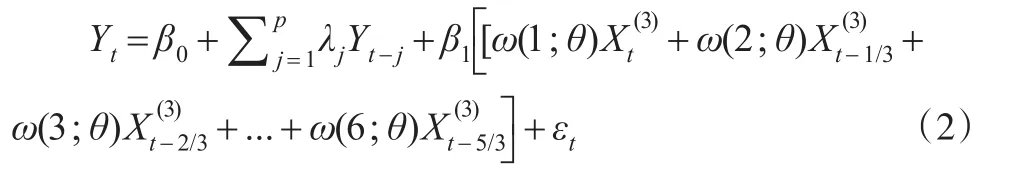
当h=1时（即向前一步预测），MIDAS混频模型可表示为：

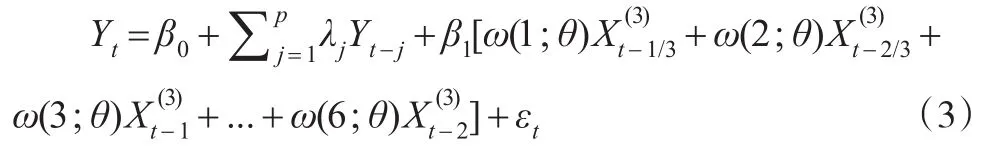
式（2）与式（3）所使用的高频解释变量的个数相同，但滞后阶数有所差异。

由于数据公布具有时滞性，例如季度GDP一般会在下个季度第一个月的中下旬公布，因此引入h步向前预测的MIDAS模型可以充分利用已公布的高频数据信息对低频数据进行预测。式（2）是根据所公布的当季第三月的高频数据信息对本季低频数据进行预测，两者公布的时间相差不大，并未解决时滞性问题。而式（3）是根据所公布的当季第二月的高频数据信息对本季低频数据进行预测，两者公布的时间相差40天左右，可解决时滞性问题，并可据此制定宏观经济政策。

本文选用beta函数作为有约束的MIDAS混频数据模型的权重函数，其权重函数形式可表示为：

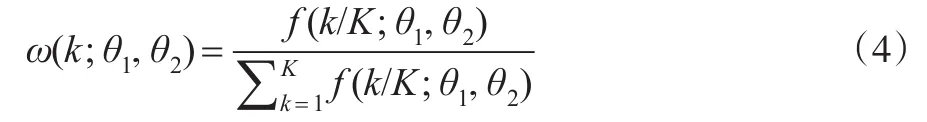
其中：

1.2 无约束的MIDAS模型（U-MIDAS模型）

所谓无约束是相对于有约束而言的，由于有时约束的设定往往是主观的，可能导致估计或预测的结果出现偏差。而由Foroni C等[3]提出的无约束的MIDAS模型，也可称为U-MIDAS模型，则不需要对滞后多项式施加约束条件，可直接用最小二乘法进行回归。无约束的MIDAS模型形式如下：

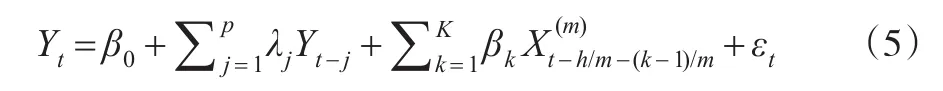
在式（5）中各变量的含义与式（1）相同，其最高滞后阶数为K+h-1。无约束的MIDAS模型在使用上有一定的局限性，一般来说，当低频变量与高频变量之间的频率倍差较小时（即m较小时），无约束的MIDAS模型较为有效，例如用季度数据与月度数据构建U-MIDAS混频模型。

2 误差修正模型简介

2.1 同频误差修正模型

由于本文仅使用两个变量构建混频模型，因此有关误差修正模型的讨论，也是基于两个变量进行分析，设被解释变量为Yt，解释变量为Xt。

由于经济中的时间序列往往是非平稳的，为避免“伪回归”，首先应对时间序列进行平稳性检验，若两个时间序列具有相同的单整阶数，那么可对这两个时间序列进行协整检验，若存在协整关系，则两变量间存在长期稳定的关系。而如果将具有长期关系的不平稳时间序列差分后变为平稳序列，再进行回归，将会损失重要信息。根据Granger定理，非平稳的变量间若存在协整关系，那么必然可以建立误差修正模型来描述变量间的短期动态关系[8]。误差修正模型的建立主要有两种方法，这两种方法的前提都是假设存在协整关系。

第一种方法是进行协整回归，得到残差项，将残差项作为误差修正项，记为ecmt-1=Yt-1---1。则误差修正模型可表示为：

再对式（6）进行最小二乘估计，求出其参数。这种方法的误差修正项可在估计误差修正模型前求出，仅须对误差修正项的系数进行估计，此时长期关系与短期关系是分两步获得的。这种方法在实证分析中应用得较为广泛。

第 二 种 方 法 是 直 接 将 ΔYt=β1ΔXt-χ(Yt-1-α0-α1Xt-1)+μt的括号去掉，有：

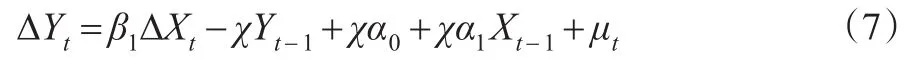
然后对式（7）进行最小二乘估计，求出其参数。这种方法不仅要估计误差修正项的系数，并且还要对误差修正项进行估计，此时长期关系与短期关系是一并获得的。

在式（6）和式（7）中，χ体现了误差修正的速度，一般情况下0＜χ＜1,且ecmt-1前系数为负数，即当Yt-1大于长期均衡解α0+α1Xt-1时，ecmt-1＞0，而-χecmt-1＜0，使ΔYt减小；反之亦然。式（6）和式（7）是Xt、Yt均为滞后一期时所建立的误差修正模型，对于滞后多期同理可得。

2.2 混频误差修正模型

2.2.1 ECM-MIDAS模型

ECM-MIDAS模型的构建，Götz T B等[4]提出了两种方法，一种是基于同频协整，另一种是基于混频协整，在这里用U-MIDAS模型分别进行说明，并令h=1（h等于其他值时同理可得）。

（1）基于同频协整构建ECM-MIDAS模型

同频协整的方法意味着从高频数据中选取某一时期的数据，将高频数据转化为低频数据，然后构建误差修正项。与同频误差修正模型的建模方法类似，也存在两种方法。

第一种方法，从高频数据中选取某个时期，将其转化为低频数据，即使用与Yt进行协整回归，其中i的取值范围是[0,m-1]。将回归残差项作为误差修正项，记为，则误差修正模型可表示为：

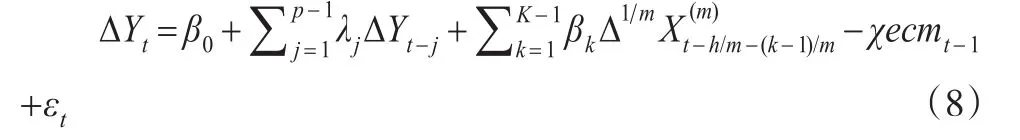
在式（8）中，Δ1/m是指高频解释变量的差分是按高频频率计算的，在本文中，即用本月值减去上月值得到差分项；与式（5）相对应，p-1为低频被解释变量差分项的最高滞后阶数，K+h-2为高频解释变量差分项的最高滞后阶数；χ与式（6）中χ的含义相同。而后对式（8）进行最小二乘估计，此时有无常数项β0均可，一般而言估计时会引入常数项，用此方法长期关系和短期关系是分两步得到的。

第二种方法，直接进行估计。

当K＞i+m（即K+h-1＞i+m）时，

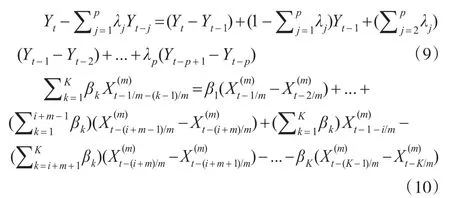
由式（5）、式（9）、式（10）整理可得误差修正模型：

当K=i+m（即K+h-1=i+m）时，误差修正模型可表示为：

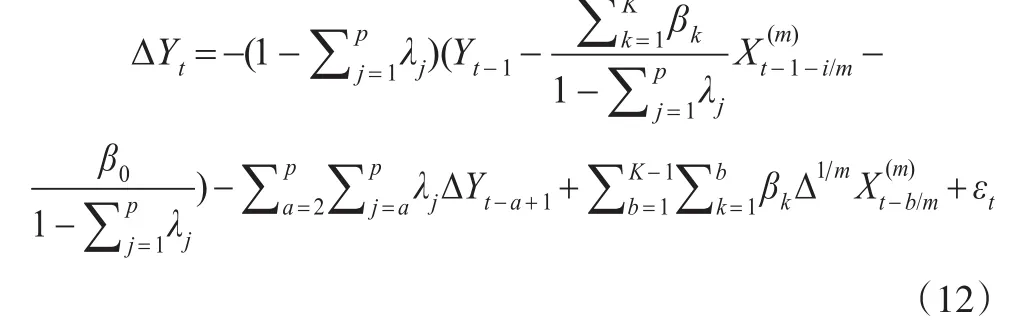
当K＜i+m（即K+h-1＜i+m）时，误差修正模型可表示为：

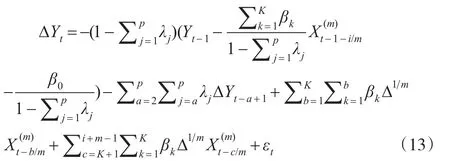
由上述两种方法所构建的ECM-MIDAS模型，长期关系中仅包含某一时期的高频数据，即误差修正项是同频形式，而短期关系中包含高频数据按高频频率计算而得的差分项。在实际应用中i的取值没有太大的影响，因为高频数据具有很强的相关性，例如在一个季度中的各个月份的经济数据，除特殊情况外不会有太大的波动。

（2）基于混频协整构建ECM-MIDAS模型

上述同频协整，高频变量仅选取某一时期，本文中即选取每个季度中第一月、第二月或第三月的数据，而混频协整可以选取更多的高频数据构造误差修正项。将式（5）进行转换可得：

误差修正项，此时长期关系中包含多个时期的高频数据，即误差修正项是混频形式，而短期关系中仅包含高频数据按低频频率计算而得的差分项，在本文中，即用本季某月的高频数据减去上季此月的高频数据得到差分项。

然而对于协整检验来说，一般都是针对同频数据，其检验方法更为成熟，因此相较于混频数据来说，基于同频数据进行协整回归，得到的长期关系更可靠；再者，式（14）的短期关系中并未包含高频数据以高频频率计算所得的差分项，因此基于同频协整构建ECM-MIDAS模型更具有准确性。为简化估计和预测的过程，本文选取式（8）作为ECM-MIDAS模型，这也是Götz T B等[4]和李会会[6]在实证分析中所运用的方法。

2.2.2 CoMIDAS模型

对于CoMIDAS模型的构建①Miller J I[5]在构建CoMIDAS模型时，令K=m_1，此时若m_=3则K=2，不能充分利用高频数据信息，因此在本文中取消K=m_1这一限制，以期选取预测效果最优的高频解释变量的滞后阶数。，在这里仍用U-MIDAS模型进行说明，并仍令h=1（h等于其他值时同理可得）。

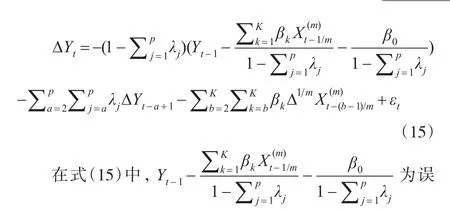
差修正项，CoMIDAS模型的方法也可看作是同频协整构建混频误差修正模型。其与基于同频协整的ECM-MIDAS模型的区别在于，ECM-MIDAS模型中长期关系的高频变量与低频变量所处时期相同，如低频变量为第一季度，则高频变量为第一季度某月；而CoMIDAS模型中二者所处的时期不同，如低频变量为第一季度，而高频变量为第二季度第二月。此时，长期关系与短期关系也可一并求出。

与ECM-MIDAS模型相一致，本文所采用的CoMIDAS模型也是分两步求出长期关系与短期关系，其公式是将式（8）中的误差修正项替换为另外，本文令h=1，p=2（即ΔYt滞后一期）②由于预测结果较多，本文仅列出h=1和p=2时的预测结果，取其他值时同理可证。，则式（8）可写为：

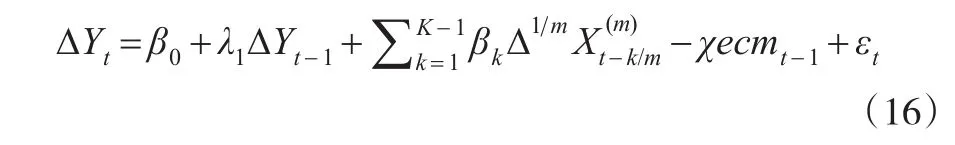
若式（16）为 ECM-MIDAS模型，则ecmt-1=Yt-1-，i是根据预测效果进行选取；若为CoMIDAS模型，则对于有约束的MIDAS模型，其混频误差修正模型的构建同理可得。

3 基于混频误差修正模型的实证

3.1 数据选取

针对我国货币与产出的关系，众多学者证实M2与GDP存在长期稳定的协整关系，并且M2是GDP变化的重要原因[9-11]，因此本文选取了广义货币M2和国内生产总值GDP作为样本数据进行实证分析。其中，M2为月度数据（2003年1月到2017年3月）来源于《中国人民银行金融统计数据报告》，GDP为季度数据（2003年第一季度到2017年第一季度）来源于中华人民共和国国家统计局。本文将季节调整后（消除季节性及不规则性，下同）的季度GDP取对数后乘以100记为gdp，季节调整后的月度M2取对数后

乘以100记为m2，m0为每季第三月的m2，m1为每季第二月的m2，m2为每季第一月的m2。gdp、m2、m0、m1、m2的一阶差分记为Δgdp、Δm2、Δm0、Δm1、Δm2。之所以对数据取对数后乘以100是因为它们在差分后，近似于增长率，具有一定的经济意义。

本文选用2003年2月到2014年3月的Δm2和2003年第二季度到2014年第一季度的Δgdp作为样本内数据建立混频模型，用于预测2014年第二季度到2017年第一季度的Δgdp，本文使用预测的均方根误差（即RMSE）来衡量预测效果，其计算公式为：

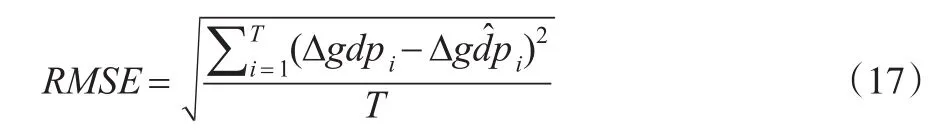
在式（17）中，i为对Δgdp预测的期数，其取值范围是[1,T]；T为最高预测期数，在本文中T=12，且当i=1时是指对2014年第二季度的Δgdp进行预测，以此类推；Δgdpi为第i时期的真实值为第i时期的预测值。

3.2 单位根检验

首先对时间序列进行单位根检验，本文所采用的检验方法是ADF检验，其检验结果如表1所示：

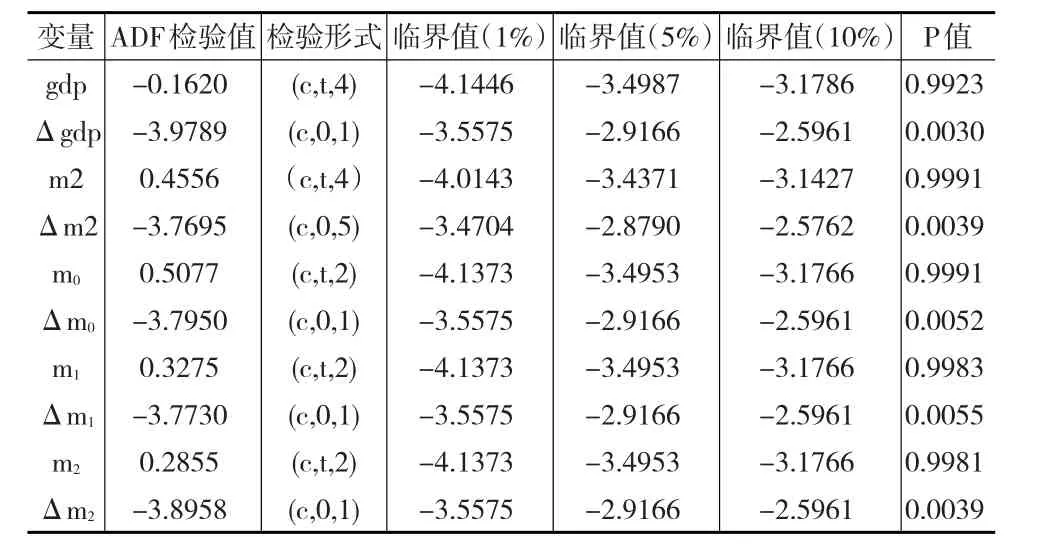
表1 各变量ADF单位根检验结果

由表1可知，gdp、m2、m0、m1、m2均不能拒绝有单位根的原假设，即时间序列均不平稳；其一阶差分Δgdp、Δm2、Δm0、Δm1、Δm2在0.01的显著性水平下均不存在单位根，即时间序列的一阶差分均为平稳序列。

3.3 协整检验

由于gdp、m0、m1、m2为一阶单整序列，因此可检验gdp与m0、gdp与m1、gdp与m2、gdp的滞后一期与m1是否存在协整关系。由于仅含有两个变量，因此可用E-G两步法进行协整检验。首先进行协整回归，求出其回归残差，分别记为e0、e1、e2、e3，而后对回归残差进行ADF单位根检验，若平稳则存在协整关系。其残差检验结果如表2所示：

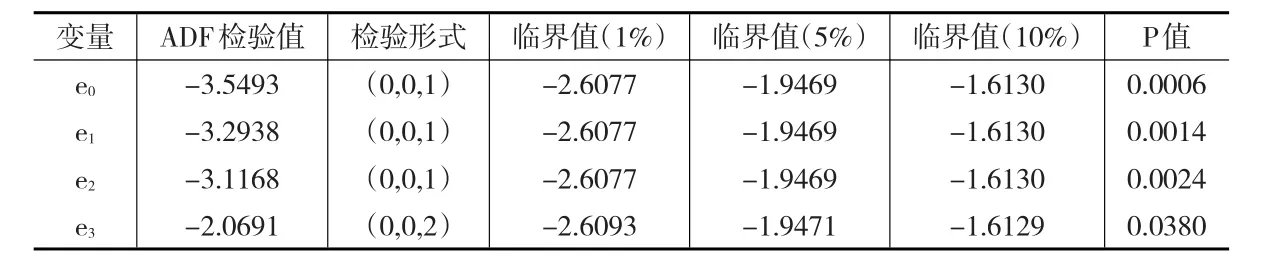
表2 残差的ADF单位根检验结果

由表2可知，e0、e1、e2在0.01的显著性水平下不存在单位根，e3在0.05的显著性水平下不存在单位根，而统计上习惯将显著性水平定于0.05[12]，因此可得：e0、e1、e2、e3均为平稳序列，即gdp与m0、gdp与m1、gdp与m2、gdp的滞后一期与m1存在协整关系，且均为（1,1）阶协整。

3.4 混频误差修正模型的有效性研究

对于ECM-MIDAS模型，其误差修正项可分别表示为：

对于CoMIDAS模型，其误差修正项可表示为：

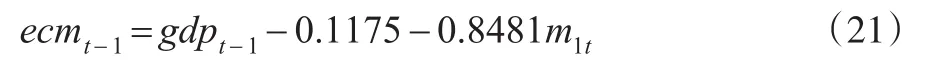
将上述四个误差修正项分别带入式（16）中，得到无约束的混频误差修正模型，其模型可表示为：若无ecm项，该模型就是将不平稳的时间序列差分后变为平稳序列构建混频模型。同理可得到有约束（本文中即权重函数为beta函数）的混频误差修正模型。对于不同的K，各个模型的RMSE如表3所示：

表3 各模型不同K值的RMSE

结合各模型的预测效果可得：

第一，U-MIDAS模型在滞后阶数较小的情况下，其预测效果要优于有约束的MIDAS模型，如表3中K=3、K=4时，这是由于U-MIDAS模型取消了滞后多项式的限制，避免了主观权重的约束；然而随着滞后阶数的增加，其预测效果不如有约束的MIDAS模型，如表3中K＞4时，这是由于当滞后阶数较高时，U-MIDAS模型需要估计的参数增多，使得模型估计能力下降，从而预测效果变差。

第二，在表3中，除了K=3时的有约束MIDAS模型外，其余模型，无论是使用ECM-MIDAS模型还是CoMIDAS模型的建模方法，在加入误差修正项后均比之前的RMSE要小，这是由于未加入误差修正项时，为进行平稳建模，取其差分项进行回归，这会损失原始数据的部分重要信息，导致预测效果不佳；而加入误差修正项后，则充分利用数据信息，根据长期关系对其进行调整，使得预测效果更优。

第三，在时间范围一致的前提下，根据AIC、BIC准则及预测精度等指标选取相较而言最优的同频自回归分布滞后（ARDL）模型求得带误差修正项和不带误差修正项的RMSE，其结果分别为：0.4056，0.6400，与混频模型相一致，在加入误差修正项后的预测效果更优。由表3，除U-MIDAS模型滞后阶数较高的情况外，混频模型的预测效果始终优于同频模型，这是由于混频模型可以充分利用各个月度数据的信息，提高了预测的准确性。

第四，当ECM-MIDAS模型的误差修正项为式（18）、式（19）、式（20）时RMSE相差不大，相较之下在有约束时式（19）的RMSE较小，而无约束时式（18）的RMSE较小。对于ECM-MIDAS模型和CoMIDAS模型的RMSE，在有约束时，ECM-MIDAS模型优于CoMIDAS模型的预测效果，而无约束时，当K=3、K=4时，ECM-MIDAS模型的RMSE较小，而K＞4时CoMIDAS模型的RMSE较小，之前讨论过当K＞4时，U-MIDAS模型待估参数增多使得稳定性下降，因此可以认为在此例中，ECM-MIDAS模型的预测效果更好。

4 结论

本文对混频误差修正模型的有效性进行实证研究，并得出了如下结论：首先，无约束的MIDAS模型适用于混频数据的频率倍差较小且滞后期较短，此时的预测效果优于有约束的MIDAS模型，反之则反；其次，混频模型比同频模型的预测更准确；再者，无论是混频模型还是同频模型，加入误差修正项后的预测精度明显提高；最后，ECM-MIDAS模型和CoMIDAS模型作为混频误差修正模型均有效，在本文的实证分析中，ECM-MIDAS模型的预测效果更好，并不是说ECM-MIDAS模型可完全替代CoMIDAS模型，而是二者可以相互补充，在不同实证分析中选取最优模型进行研究。