把握评价导向诊断改进教学——基于“四基”课程目标的评价探索与结果分析

◇苗东军

作为基层教研员，为发挥评价的导向功能，引领一线教师重视基本思想和基本活动经验目标的落实与评价，笔者在为一线教师提供的期末质量调研试卷中，加强对“基本思想和基本活动经验”以及“四能”的评价探索。希望通过评价导向，引领一线教师全面、准确地把握教学目标，探索能力与素养培养落地生根的方法，积累相关经验，以切实提高学科教学质量。下面以2016—2017学年下学期我市六年级学业质量调研考试中学生出错率较高的几道题为例，谈谈基于“四基”课程目标的评价导向与结果分析，以帮助老师找准课改的难点和薄弱点，促进老师扎实有效地开展教学实践探索，不断深化学科课程改革。

例1：太阳到地球直线距离的平均值为149597870.7千米，光速大约是30万千米/秒。光从太阳到达地球大约需要（ ）秒（保留整数）。

【命题意图说明】

本题是《数学课程标准（2011）》附录例23的内容。例23的说明中明确指出：在计算的过程中，要合理利用数的单位和度量单位来减少位数。在解题思路方法上，本题还能反映教与学的过程与方法。具体表现为：如果理解掌握了大数的意义及简便计算的方法，就可以把“149597870.7千米”改写成“14960 万千米”，从而列出“14960÷30”来计算答案。如果学生简便计算的意识强烈，还会进一步把“14960÷30”转化为“1496÷3”来计算（既可以直接利用计数单位来转换，也可以在前式的基础上，利用商不变的性质进行转换。在列竖式计算中，学生也有这样的经验）。

本题有两个考查点：一是除法意义的应用；二是简便运算的意识，以及简便运算时根据“大数的意义”进行运算推理的能力，也可理解为高级的运算能力。显然，这些考查点都指向了学生的数学思维经验与思维能力，仅靠死记硬背获得的知识和技能难以顺利解决。

【测试结果分析与建议】

本题的错误率达49.5%，位居试卷首位。学生的错误主要有两类：（1）149597870.7÷30≈4986596（秒），没有考虑两个数量的单位不同，不能直接相除；（2）在统一两个数量的单位时发生错误，错误地将“149597870.7千米”改写成“149.6万千米”或“1496万千米”，求出的答案为5或50。

学生的两种主要错误正好对应着两个考查点。第一种情况从表面看是不认真、粗心造成的，实质上是对“包含除”的意义理解不透所致。如果学生真正理解了“包含除”的意义，就能正确建立“路程÷速度＝时间”这一数量关系模型，理解其中各数量单位的意义和要求，列式时自然要统一被除数和除数的单位。第二种错误就是运算推理能力弱，或者是思维习惯差，完全靠记忆和教条的经验，而没有通过仔细的推理进行换算。

例2：48公顷=（ ）平方千米。

【命题意图说明】

此题不仅能考查两个单位之间的进率及其相互换算，更想考查的是“数学思考”和“问题解决”目标的达成情况，重在对思维能力和问题解决过程与方法的考查。很多版本的教材虽然给出或让学生探究了二者的进率，但学生并不易掌握，解答时就需要学生在理解掌握概念的基础上，借助思维的经验，灵活运用概念进行运算推理来完成单位转换，本题就具有了一定的探究性和挑战性。

解答时有两种思路：（1）间接转换。既可以先把公顷换算成平方米，再把平方米转换成平方千米，也可以先把平方千米换算成平方米，再把平方米转换成公顷。（2）直接转换。可以从概念入手，直接探索公顷与平方千米之间的进率，找到进率后直接换算。这里，也分为两种思路：一是探索1公顷等于多少平方千米；二是逆向探索1平方千米等于多少公顷。具体方法也有两种：一是根据两个面积单位（1公顷和1平方千米）边长之间的关系计算得出面积之间的关系；二是用平方米来统一两个面积单位的计量，再换算。

【测试结果分析与建议】

本题的错误率达39%，位居试卷第二位。作为样本的班级之间的差异明显：错误率最高的达91.7%，最低的才4.7%；错误率高于40%的班级数占抽调班级数的一半，高于53%的班级占28.6%。错误答案有 4800、48000、480000、0.048等。

关于错误原因，多数一线教师认为：（1）小数点移动方向没掌握，进率记忆不准；（2）平时对公顷和平方米的进率运用较多，印象深刻，而忽视了平方千米与公顷的进率，马虎造成错误。

老师对错因的分析，暴露了老师对“四基”目标认识的模糊和落实的乏力。这正是造成学生知识记忆负担过重、靠记忆而不是靠理解掌握知识、靠套路解题而不是灵活运用思想方法解决问题的根源，也是学生大面积出错的根本原因。这在对老师的访谈中也得到了印证：凡是老师对“四基”目标认识和落实到位的，学生的正确率就高；老师认识和落实不到位的，学生的错误率明显较高。

例3：观察图1，将阴影部分与整个图形面积的关系分别用分数、最简整数比、百分数表示：(保留一位小数）。

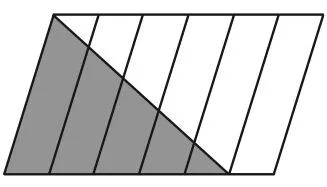
图1

【命题意图说明】

考查学生综合运用知识解决问题的能力。具体表现为：从图中读取有用数学信息的能力，分数、比、百分数意义的理解和运用，分数乘法的理解及运用，三角形和平行四边形面积公式的理解和运用。

解答的关键是先正确求出分数或比，不同水平的学生可以用不同的方法。（1）根据分数的意义得出分数表示的结果。用这种方法需要读出以下信息：涂色部分是左边5格面积的一半，如果表示成图2的样子，就很容易用表示出阴影部分与整个图形面积的关系。（2）用分数乘法计算得出。用这种方法需要读出两个关键分数——涂色部分是整个图形的的，这种方法看似简单，但对基础知识的理解掌握水平、对应用意识和能力的要求都较高。（3）用面积公式求得。如图3，如果用h表示整个平行四边形的高,用a表示它的底，那么阴影部分的面积就是ah,容易得出它是整个平行四边形面积的。

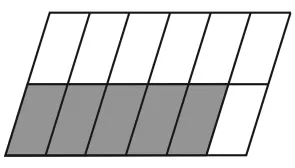
图2

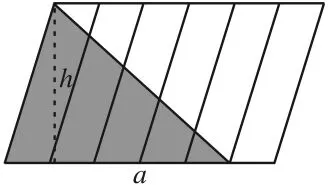
图3

本题看似简单，实际上对学生的数学抽象能力要求较高，能较好考查学生的“四基”“四能”。

【测试结果分析与建议】

此题失分率为35%。班级间的差异也很明显：错误率最高的达71.4%，最低的为17.1%。错误答案五花八门，有等。

错误原因主要是不能根据问题解决的需要从图中读取有用的数学信息，不知从哪儿入手去求二者之间的数量关系。反映在教学中，就是我们没有真正把数学语言，如“分数”“分数乘法”意义的文字、符号、图形表征的学习列入学习目标之中，加强不同表征之间的联系与沟通，帮助学生透彻理解和掌握基础知识。这一判断在一线老师的考试分析中也得到了印证，没有老师从这一教学缺失的角度来分析查找原因。

从以上错误答案中，还可分析出学生没有数感、缺乏对问题解决过程与结果进行自我评价与反思的习惯与能力等。如，通过图形可以直观看出，、等答案是明显错误的，但并没能促使学生进行自我诊断与改进。

例4：一个棱长8厘米的正方体，如果从一个顶点处挖去一个棱长2厘米的小正方体，剩下部分的表面积与原来的表面积相比（ ）。

A.没有变 B.增加了 C.减少了

【命题意图说明】

此题重点考查学生的空间观念和推理能力。空间观念的具体表现有三个层次：一般水平表现为能够根据语言描述想象出变化前后的两个图形，只有学生明白图形是什么，才能知道要求的问题是什么，进而正确解答问题；较高水平表现为在正确想象出两个图形后，还能够正确想象出两个图形表面是由哪些面组成的，能正确列式表达两个图形的表面积；更高水平表现为能对组成两个图形表面的所有面进行关联，根据需要想象出它们的对应关系。逻辑推理能力表现为解答方法的逻辑性和灵活性。在两个表面积的比较中，既可以通过计算它们的具体面积进行比较，也可以不具体计算，通过对应面之间的相等关系进行比较。在具体计算挖去后的面积时，由于面的数量增多，需要学生有序地去找，避免重复或漏掉。

【测试结果分析与建议】

本题错误率达34.2%。班级之间的差异也很明显：错误率最高的达65.5%，最低的为11.7%。错误类型有：（1）空间观念发展不够，想象能力较弱，根据语言描述想象不出两个图形的样子，弄不清题意。（2）缺乏理性思考习惯和能力。错选B选项的较多，这些学生感性地认为，挖去小正方体后，露出的面多了，没有全面、理性地具体分析表面的变化情况，错误地认为表面增加了。（3）思维的逻辑性较差。因无顺序地思考问题，在算表面积时重复或漏掉了一些面。

本题的错误反映了教学中空间观念、理性思考习惯和能力的培养落实不力。空间观念的形成，需要丰富的操作活动经验和观察、描述、想象、表达等思维活动经验，能够在相应的语言、实物、图形、表象之间建立起正确的联系。为达成这一目标，教学中应充分利用教具、学具，给学生充分的操作、观察、想象、描述、交流的机会，在活动中建立表象，培养和发展学生的抽象能力和空间想象能力，建立空间观念。理性思考习惯包括：在新知学习中，多思考为什么，多发现、归纳相关知识之间的区别与联系；在问题解决时，对所列的每一个算式，做出的每一个判断、运算、推理、变形，都要想依据、讲道理；对问题解决的结果，要进行自我评价和反思，优化和完善过程和方法，发现问题后要查找原因、改进方法、进行再尝试和再评价，直至圆满解决问题。

例 5：面积估测。（如图4）如果左边的小正方形的面积是1平方米，请估测右边长方形的面积约为多少平方米。

图4

【命题意图说明】

本题重点考查面积计量的基本方法，旨在对过程与方法的考查。有两种解答思路：一是直接计量。直接用作为标准的小正方形同长方形进行比较，通过估算铺满长方形的小正方形的个数，得出结果。如果是估测，不追求结果的精确性，只要合理即可。如果借助刻度尺画图计算，结果会精确一些。二是间接计量。先用小正方形的边长同长方形的长和宽进行比较，算出长方形的长和宽后，再算出长方形的面积。在计算中，由于涉及图上距离与实际距离的换算，需要用到比例的相关知识，这对学生灵活运用知识的意识和能力都进行了考查。

基于上述评价意图，本题的评价重点就应该是问题解决的过程与方法，对于学生估测的不同结果，只要是依据自己确定的、合理的问题解决方案得来的，都应得到肯定。

【测试结果分析与建议】

本题暴露的最大问题是教师的教学与评价能力问题。尽管下发有统一的评分指导与说明，但很多老师没弄清本题评价的重点，评判时仍然只关注结果（答案）的对错，不关注问题解决的过程与方法，以及在问题解决过程中所表现出来的能力和素养。如图5所示的解法，很多学生是用直接计量的方法，通过计算铺满长方形的小正方形个数来估算。为使估算值更加准确，图7还估计了不是整行（列）部分约是5个小正方形的大小，这种极具智慧和个性的解决方案，却因答案与老师的不符合，被判为错误答案，没有给分。而图8所示的解法，答案虽很接近老师想要的答案，但从书写的解答过程中，看不出长方形的长和宽是否与小正方形的边长进行了比较，图上也没有任何痕迹，这样的解答过程，反映了学生缺乏度量意识和逻辑性，问题解决的过程与方法不正确，计算出来的结果并不能表示长方形的实际面积。因为试卷上小正方形的边长约为0.9cm，长方形的宽约为3.7cm，这样长方形的宽实际长度就约为4m，这个4m应该是根据比例尺得到的，而不是四舍五入得到的。这一解法，阅卷老师竟然还给了一半分。这种对命题意图的误解，本质上反映了老师教学理念与行为的脱节、对“四基”课程目标认识的模糊和实践的乏力。

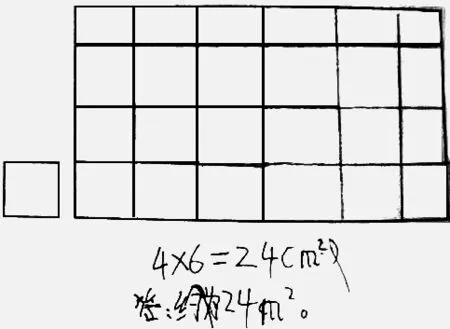
图5

图6

图7

图8