关注“量”，思考“质”，促进“行”——以“区域教育质量健康体检”项目为例谈

◇刘克臣

教育部“区域教育质量健康体检（小学数学）”项目的评价对象是小学四年级学生，力求通过科学的大数据分析，透析小学数学教育质量的整体情况，从而促使教师的教和学生的学更加有效。下面从一个项目亲历者的角度与大家分享研究和实践过程中的思与行。

一、搭建科学的测试框架是评价的基础性工作

搭建测试框架是评价过程的重要内容，决定着评价的效果。课程标准是搭建测试框架的重要依据，其中明确提出了两个最基本的领域：内容领域和能力领域。为了使评价内容更加明确，避免彼此交叉，将《义务教育数学课程标准（2011年版）》（以下简称《课标》）中的内容领域和能力领域分别整合成三个方面，具体内容如表1和表2：

表1 内容领域

表2 能力领域

搭建测试框架还有一项工作就是制定全面的、可操作的评价标准，并作出清晰的描述。例如表3是关于“问题解决”的评价标准描述。

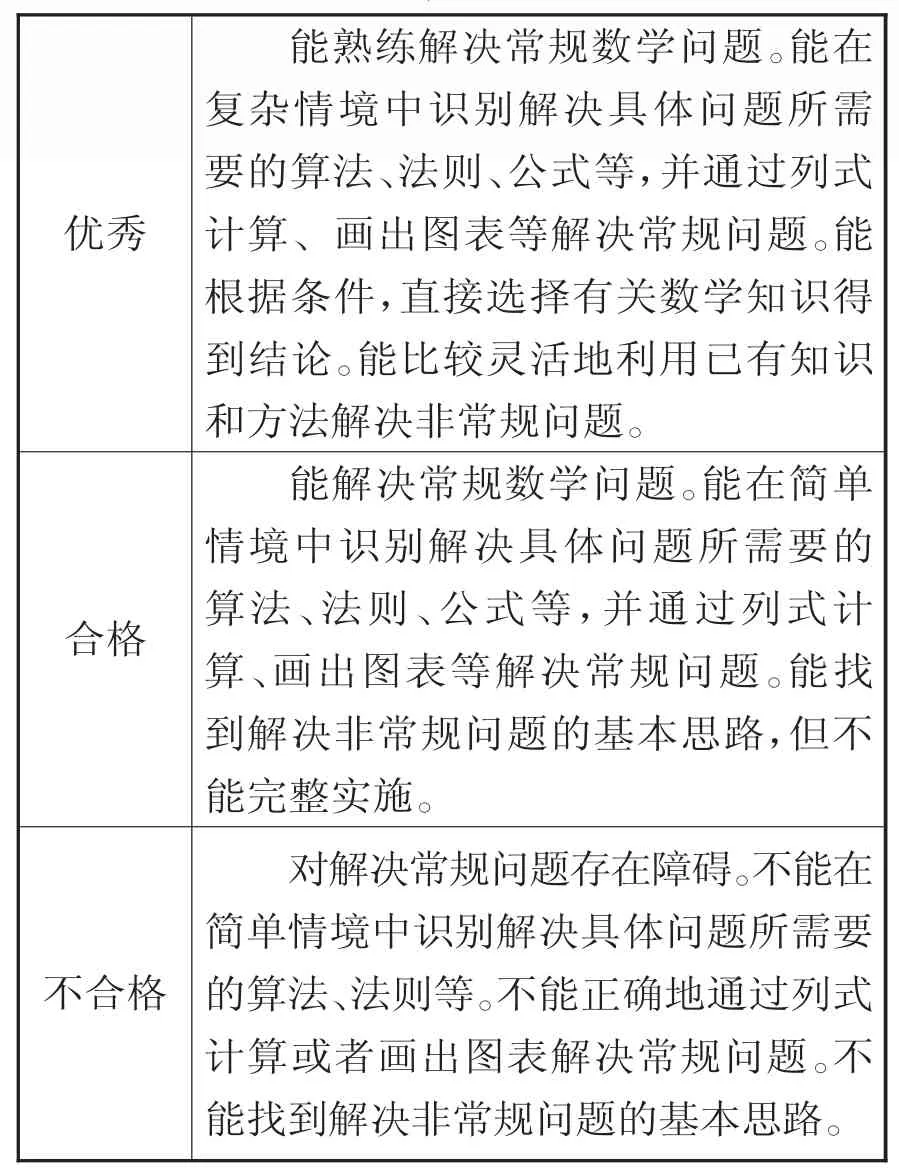
表3

除此之外，为了适应评价改革的发展，结合学生发展核心素养也可以尝试划分素养维度，用以评价学生的数学素养。例如，下面是结合四年级学习要求，用统计的方法划定的七个素养维度（如图1）。

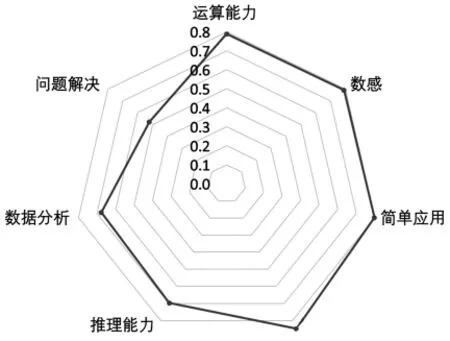
图1

从图1中的数据统计分析看，本次评价除问题解决这个维度外，其余几个维度学生均表现优秀，说明问题解决依然是数学学习的一个短板。

二、基于评价框架精雕细琢评价题目

研制试题是评价的核心环节，正式进入命题之前命题者要深入思考三个问题：（1）我们期望学生学会什么？（2）什么样的学生表现表明学生达到了要求？（3）什么样的测评问题能够有效地测评学生的表现？

基于对以上三个问题的思考，命制试题时要处理好以下问题：

1.基于《课标》，把握问题的难易度。《课标》描述的是合格水平标准，即每个学生都要达到的要求。目前，小学阶段的测试性质大多属于水平测试。这就要求试题的难易度要严格用《课标》衡量，低于标准的问题和远远高于标准的问题都是没有意义的。一般情况下，严谨的测试会在正式测试之前安排预测试环节，用来检验题目本身的合理性，其中难易度就是重要的关注指标。

2.素材联系生活实际，注重体现时代性。测试题目中，如果有紧密联系实际的问题，会使学生产生亲切感，体会数学知识解决问题的价值。

例1：王阿姨乘坐G157次火车从北京南站到南京南站，到达时间是23时24分。她想知道这列火车一共行驶了多长时间，需要从火车票上找到的信息是（ ）。

图2

A.17：44开 B.3月30日

C.748.5元 D.2车14A号

3.关注思维，外显学生的思考过程。图3是学生数学素养的考查层次。

图3

从中看到学科思维处于最顶层的位置，说明思维的发展特点是评价的重要着眼点。因此，命题要充分考虑如何外显学生的思考过程。要使学生的思维外显，就要提供开放的表达机会，促使学生依据自己的理解进行个性化的表达。例2这个问题给学生提供了借助图形表达思路的机会。

例2：一种洒水车（如图4），洒水的宽度是7米，每分钟行驶100米。

图4

（1）一辆这种洒水车行驶1分钟，地面洒上水的面积是多少平方米？

（2）一条路长2500米，宽7米（如图5）。如果用两辆这种洒水车同时工作，10分钟后能给这条路的表面都洒上水吗？请把你的思考过程写在下面。

图5

下面图6是两个学生对第二问的作答情况：

图6

从图6中看出两个学生的思维特点截然不同，第一个学生属于“数量关系清楚，中规中矩型”，第二个学生“善于借助直观，思维更加灵活”。这样的考查形式给学生提供展示个性化思维的机会，思维特点必然暴露。

4.既关注学习的结果，也关注日常学习过程。“既重视结果的获得，也重视获得结果的过程”，这是《课标》的重要理念，也是培养学生能力的重要途径。通过评价引导老师更加关注学习过程，也是命题时一个重要的思考方面，比如例3。

例3：强强想知道△ABC内角和的度数，下面拼法中正确的是（ ）。

图7

这个问题没有直接考查三角形内角和等于180°这个结论，而是关注学生是否经历了三角形内角和的探索过程。如果在日常教学中，教师没有给学生提供动手实践的机会，学生没有真正经历这个过程，那么问题一定会暴露出来。

5.注重学生发现问题和提出问题的考查。近几年的监控评价中都设计了让学生发现和提出问题的题目，比如例2中的第3小题：

（3）结合题目中的信息，请你先提出一个简单的数学问题，再提出一个富有挑战的数学问题。（不用解答）

简单的问题：_________________________

富有挑战性的问题：___________________

看学生的主要作答情况（如图8）：

图8

连续几年的测查已经提醒我们：发现和提出问题是一种重要的能力，我们需要在平时教学中加强实践和研究。

三、用好数据这面“镜子”，全面、深入地进行分析

1.标准差让我们重新认识平均分。

以往考查结束后，老师们最关注的是平均成绩。多年以来，正是平均分这一单一指标的评价，造成了老师、领导、家长只关注结果，忽略了平均分背后的信息。标准差的引入，将会对平均分有更加具体的诠释。

如果说平均分反映一个群体的集中量，标准差就是反映这个群体的分散的量。通过标准差可以了解到学生的分化程度，是对平均分的具体化。举一个例子说明一下。

有两组数据： 5、6、8、9；1、2、12、13。 这两组数据的平均数都是7，但是第一组数据的标准差约是1.6，第二组数据的标准差约是5.5。比较发现，虽然平均数相同，但是明显第一组数据比较集中（向平均数靠拢），第二组数据比较离散。说明第二组的学生中有成绩突出的，也有个别学习水平较低的。对于授课教师来说，第一组比较容易统一授课标准，第二组就要关注差异。可见，标准差可以更加具体地概括出学生水平分布，为老师改进教学策略提供依据。

2.利用领域得分率分布图了解学生具体内容的学习情况。

图9是某地区四个领域得分情况的统计图。

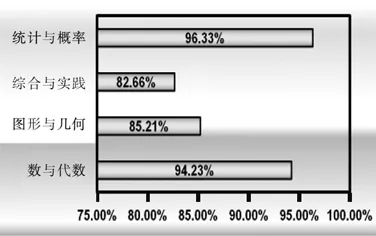
图9

通过统计图，可以清晰地看到四个领域的得分率都在80%以上，以往的分析只能到此，然而每一个领域得分率具体分布情况如何呢？在这个领域中学生的整体水平是比较集中还是两极分化呢？因此，得分率分布图就显得十分有价值。下面以内容领域得分率分布图作简要介绍。

图10为盒形图，横轴表示领域，纵轴表示得分率。将四个领域维度所有学生的得分率按从高到低的顺序排序，其中最上面第一条横线表示5%的学生得分率高于此线对应的得分率；第一个矩形上沿对应的得分率表示25%的学生的领域维度得分率高于此线对应的得分率；两矩形中间的线表示50%的学生得分率高于此线对应的得分率；第二个矩形的下沿对应的得分率表示75%的学生的领域维度得分率高于此线对应的得分率；最下面的线表示95%的学生的领域维度得分率高于此线对应的得分率。两端的线之间距离在一定程度上描述了本地区学生得分率离散程度的大小。得分率分布图和得分率之间的关系犹如平均分和标准差的关系，得分率分布图将得分率细化，使老师更加明确该领域学生学习的具体情况。

图10 各领域得分率分布图

3.总学业水平与各领域学业水平关系的分析，彰显个性化诊断。

总学业水平和各领域学业水平关系的分析，指向个性化的评价。这个分析维度将学生的总学业水平细化，通过分析看出学生到底“优在何处，差在哪里”。例如，图11是图形与几何领域与总学业水平关系图。

该图横轴表示总学业水平的四个等级，纵轴表示人数百分比。通过该图看到，总成绩优秀的学生在图形与几何方面表现比较突出，也存在差异。有的学生虽然成绩达标，但是在图形与几何领域的成绩却是优秀。这样的信息，让总成绩较好的学生明确努力方向，让总成绩不好的学生明白自己的强项，同时促使教师真正做到因材施教。

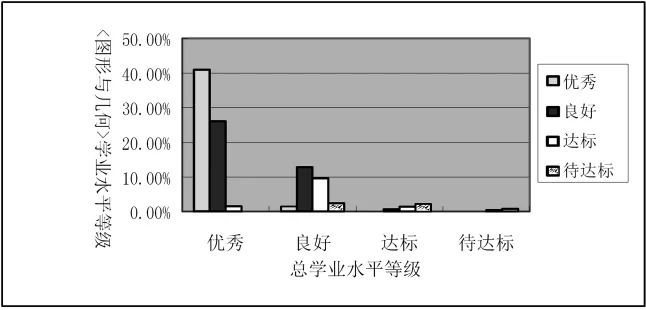
图11

4.发现影响学生学习的因素。

影响学生学习的因素有很多，比如学习兴趣、师生关系、自我效能感、学习焦虑等。评价除关注学科本身指标外，还应该关注影响学生学习的其他因素，例如图12。

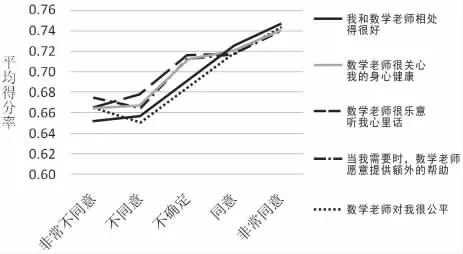
图12

图12反映的是师生关系对于数学学习成绩的影响。通过该图发现，随着师生关系越来越好，学生的数学学习成绩也越来越好。当学生认为师生关系最好的时候，学生在所有题目上的平均得分率最高。这说明良好的师生关系是影响学生学习的重要因素。

评价是落实“核心素养”培养的重要保障。改革评价制度，以评促改，应以高利害的杠杆来撬动、激发和促进教学方式和学习方式的转变，继而形成更适切的人才培养模式。对于小学阶段，应该看到评价的导向变化，着眼于人的持续发展，将评价工作引导到正确的道路上来。