在“问题解决”中提升数学思维素养

◇陈金飞

数学学习的最终目的在于问题解决和实践应用。在“问题解决”教学中，主要培养学生对简单的问题进行初步的分析、综合、抽象、概括，让学生逐步学会有理有据地思考问题。那么，如何通过复习，让学生在问题解决过程中进一步经历“数学化”与“再创造”的过程，激活问题解决的策略意识，提升问题解决能力呢？

一 梳理归纳，沟通联系，形成系统

复习中要注意为学生提供自主梳理知识的时间和空间，引导学生对所学知识进行系统整理，在不断梳理、调整、完善的过程中构建知识体系。梳理时，可以为学生提供这样的脚手架：回顾小学阶段，你学习了哪些解决问题的策略？每个策略分别适用于解决哪些问题？使用这些策略解决问题有什么好处？学生根据老师提供的线索，提取头脑中已有的策略，再现解决问题的过程，进一步体悟到使用策略的优势。在展示学生的作品（如图1、图2）过程中，需要注意反馈的顺序：一般先反馈有问题或者不完善的作品，可以引发学生修正完善，最后形成完整的知识网络。

图1

图2

二 典型引路，经历过程，内化策略

学生问题解决能力、策略意识的形成不可能一蹴而就。我们利用复习阶段，从策略知识的整体出发，精选典型习题，激发学生积极思考，让学生经历策略提升的过程，内化对策略的认识。对于某个问题，利用何种策略解决？在什么条件下可以使用这个策略解决问题？还可以使用别的策略解决吗？设计有联系性的题组进行比较练习，在比较中再次经历策略形成和发展的过程，不断体悟策略应用的妙处所在，潜移默化中将策略内化于心，从而悄然提升学生问题解决的能力。

例1.不计算，你能很快说出求“下列各图形中阴影部分面积”时哪些需要用转化策略，哪些不需要吗？为什么？（如图3～图6）

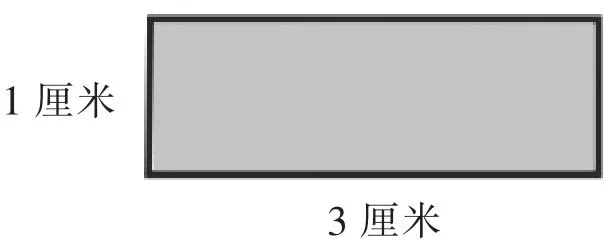
图3

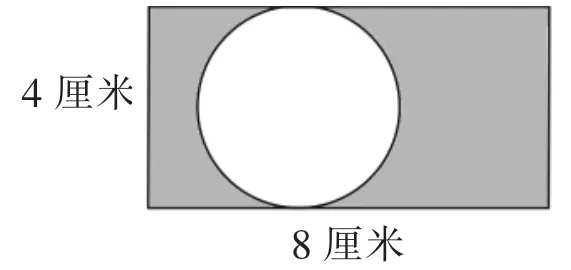
图4

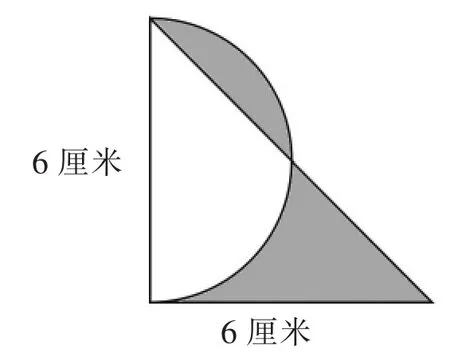
图5

图6

图3直接利用长方形面积公式计算，图4用长方形的面积减去圆的面积，所以这两道题都不需要用转化的策略。图5、图6都不能直接求出阴影部分的面积，所以需要用转化的策略，把不规则图形转化为规则图形。图5可以把阴影部分合在一起，转化成三角形，面积正好是底和高都是6厘米的三角形面积的一半。图6则可以利用三角形内角和是180度，将三个扇形合在一起，转化为一个半径为2厘米的半圆。

例3.你能根据下列关键句进行合理转化吗？（1）男生人数是全班人数的。

（2）学生饲养小组养的白兔与黑兔只数的比是 4∶5。

（3）学校10月份的用电量比9月份节约了10%。

此环节引导学生从部分与部分、部分与总体以及分数、比、百分数等不同的方面考虑，启发学生多角度思考，提升学生有效转化的思维能力。

三 适当拓展，综合贯通，提升思维

问题解决教学的目的在于使学生掌握多种问题解决的策略，解决现实生活中的问题，不断提高学生问题解决的能力。深化与拓展不仅是对数量关系认识的提升，更是理解知识、运用知识、提升思维能力的必经之路。设计解题策略不唯一的问题，可以激发学生从多角度思考，培养学生思维的广阔性、灵活性、独创性。

例4.盒子里有80枚白子和50枚黑子。每次取走3枚白子，同时放入3枚黑子，像这样取放多少次后，白子与黑子的数量正好相等？

我们可以采用枚举的方法，把所有情况用表格列出来，看哪一种情况符合要求。

原来 取放1次后 取放2次后 ……白子/枚 80 77 ……黑子/枚 50 53 ……相差/枚 30 ……

也可以引导学生通过观察和比较，发现：每次取走3枚白子，放入3枚黑子后，棋子的总数不变，但白子和黑子相差的枚数每次减少6。可以列式（80-50）÷（3×2）算出需要取放的次数。

也可以这样思考：每次取走3枚白子，放入3枚黑子后，棋子的总数不变，当白子与黑子正好相等时，两种颜色的棋子数各65枚，根据白子减少的总数，可以求出需要取放的次数。列式（80+50）÷2=65（枚）；（80-65）÷3=5（次）。

还可以列方程解答，设需要取放x次。列方程80-3x=50+3x。

从这道题的解法中，可归纳出多种策略——列表、假设、方程等。教师要引导学生分析与比较，体会如何从问题中抽象出概念模型，进而优化问题解决的策略。

四 加强反思，感悟思想，发展思维

在平时的复习教学中发现，一些学生“一听就懂，一做就错，一点就会”。看似粗心、马虎，其实质是学生对问题情境理解能力薄弱，加之缺乏反思检验的习惯，使得原本可以避免的错误得不到及时发现和纠正，这不利于培养学生问题解决的自信心。数学学科的抽象性特点决定了学生不可能一次性地把握知识的本质，需要学生在不断反思的过程中，逐步加深对知识的理解。

在复习阶段，一是要重视学生对解决问题过程的反思，即引导学生在解决问题的过程中时时进行反思；二是要重视学生在解决问题后的回顾，引导学生回顾解决问题时运用了什么策略，思考解决这一问题是否还有更好的策略，让学生在不断反思中提升问题解决能力。在反思环节，可以组织学生开展小组讨论，同学之间彼此相互启发，碰撞出思维的火花，提升思维水平。

我在“假设”策略的复习教学中，先后三次引导学生及时反思，使学生深刻感悟假设策略、提升化归思想。

例5.（1）小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。已知小杯的容量是大杯的,小杯和大杯的容量各是多少毫升？

（2）小明把720毫升果汁倒入5个小杯和2个大杯，正好都倒满。1个大杯的容量比1个小杯的容量多45毫升。小杯和大杯的容量各是多少毫升？

学生的第一次反思：“解决问题过程中用到了什么策略？”“为什么两个量之间不管是倍数关系还是相差关系，都可以用假设的策略？”在比较反思中内化已有知识结构，明确倍数关系、相差关系两种不同类型的假设的特征，题中出现两种未知量，两种未知量之间存在着关联，那么就可以把两种未知量转化成一种未知量。

例6.小明把720毫升果汁倒入5个小杯和2个大杯，正好都倒满。3个小杯的容量等于2个大杯的容量。小杯和大杯的容量各是多少毫升？

学生的第二次反思：“解决这个问题用到了什么策略？”“你是怎样假设的？”“为什么都是假设成小杯？”在反思中，让学生明白如果假设全是大杯，就要把小杯转化成大杯，5个小杯换成个大杯，不是整数，计算烦琐。从而感悟到在使用“假设”策略时，要选择简便的转化方法。

例7.小明把720毫升果汁倒入4个小杯、1个中杯和1个大杯，正好都倒满。大杯的容量是小杯的3倍，中杯的容量是小杯的2倍。小杯、中杯、大杯的容量各是多少？

学生的第三次反思：“题中出现三种未知量，可以假设成一种未知量吗？”让学生在不断接受挑战的过程中，思维不断深入，明确假设的真正价值在于使问题简单化，从而在提升学生策略水平的同时，感悟数学思想，发展数学思维。