指向数学理解的小学数学命题的探索

◇包静娟

一、数学命题为什么要围绕数学理解进行？

2017年3月，笔者对市区某校进行数学学业质量调研，其中一道题是这样的：有个小朋友叫小明，他拖了一辆玩具汽车去公园玩，车上有5只小鸡、10只小鸭，请问小明有几岁。

调查的结果(如表1)使人震惊，不管是一年级还是三年级，正确率都不足10%。为什么我们学生的问题解决能力如此薄弱？南京师范大学郝京华教授认为，我们的学生患上了“脆弱知识综合征”。评价可以实现价值的引领，从这个角度看，基于数学理解的命题有着重要的意义。

表1

二、基于数学理解的命题的维度是什么？

数学理解包含两层意思：一是“对数学对象的理解”，即学生对数学的知识内容、方法技巧、思想策略等的理解；二是“从数学的角度去理解现实”，这是一种更深层次的数学观念的形成。理解是多维的和复杂的，有不同的类型和方法。数学理解的测评，不局限于了解学生已经学会了什么，还要测评学生能在多大程度上在新情境下灵活应用所学的知识。具体可以从数学理解的五个维度进行命题：

1.能解释。通过归纳或推理，系统合理地解释现象、事实和数据，洞察事物间的联系，并提供例证。

例1：老师和同学们一起开展植树活动，老师每人植2棵，学生每2人植1棵。这次活动一共植树19棵，可能有几位老师、几名学生参加植树活动？（可以列式计算，也可以画一画）

2.能阐明。叙述有深度的故事；提供合适的转化；从数学、文化、历史角度或个人角度，揭示观点和事件的含义；通过图示、类比和模型等方式，达到理解的目的。

3.能应用。在各种不同的真实情境中，有效地使用和调整学到的知识。

例3：根据下面图1中四幅图的规律，第5幅图中有（ ）个●，（ ）个△。

图1

4.能洞察。能以批判性的眼光去看待、分析各种观点；运用所给的既定事实推断出结论。

例4：三年级女生做仰卧起坐。1分钟做40个以上（含40个）为优秀，做21～39个为及格，做21个以下为不及格。三（1）班女生1分钟仰卧起坐成绩统计如表2。

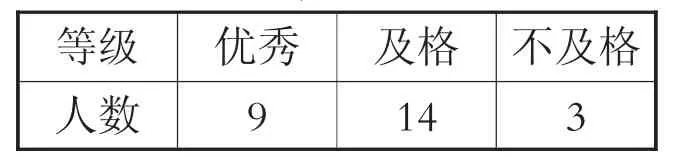
表2

（1）芳芳的成绩在三（1）班女生中排名第7。她可能做了多少个？请在合适数量后面的□里面画“√”。

38个□ 27个□ 43个□ 39个□

（2）请写出你选择的理由。

5.能自知。显示元认知意识；察觉诸如个人风格和思维习惯等促成或阻碍理解的因素；意识到我们不理解的内容；反思学习和经验的意义。

例 5：平平在计算 435÷35 时，把“35”抄成了“5”，并计算出了结果。他想要得到正确的结果，应该再（ ）。

A.乘7B.乘30C.除以7D.除以30

三、数学理解视角下的命题，必须实现哪些方面的转变？

1.从“外显”走向“内隐”。

以往的考试，试题主要测评的是知识的识别和记忆。知道不等于理解，仅仅考查显性化事实性知识的再认和复现，无法准确反映学生对知识的掌握程度。为了让学生获得有意义的发展，试题在考查外显知识的同时，还要考查学生对知识的本质内涵、意义价值的深刻理解和灵活应用，把内隐素养的考查放在重要位置，实现从“记忆”向“理解”的转变。

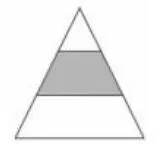
图2

【分析与思考】学生在解答这道题的时候，正确率比较低（如表3）。究其原因，是教师的教学行为形塑了学生的思维。传统课堂教学中，教师呈现的分数图例，平均分的每一份的形状都是一样的，导致学生一看到形状不同，就误以为不能用分数表示。实际上，分数表示的是平均分的总份数和表示的份数之间的比例关系。在这里，与面积有关，与形状无关。此题可以较好地检测学生对分数意义本质的理解程度，等积变形的数学思想渗透其中（如图3）。

表3

图3

2.从“孤立”走向“联系”。

Capenter(1999)指出，数学理解的发展意味着，学生头脑中建构更加丰富、更加具有整合性的知识结构，这种整合的知识结构使得学生的数学理解更富有生成性。

联系是数学理解的本质。基于数学理解的试题，不能停留在对孤立知识的单一评价上，要在数学各知识之间、数学与其他学科之间、数学与生活之间建立联系，创设融通联结的开放空间，让学生进行多元表征，以此评估学生对数学的理解。[例7是江苏省2016年义务教育学业质量监测三年级调研（无锡）卷中的一道题]

例7∶学校举行广播体操表演，每行有12人,一共有16行，小明通过竖式计算知道一共有192人参加表演。（如图4）

图4

竖式中箭头所指的可以用下面图（ ）框中的点来表示。

【分析与思考】本题让学生用点子图来直观表征乘法竖式的算理，“用十位上的1乘12，结果应该是120”。抽象的乘法竖式与直观点子图的连接，让数与形完美结合，借助形象理解抽象，加深了学生对位值制的理解。

3.从“结果”走向“过程”。

数学是思维的体操。学生对数学的理解程度通常在过程中展现出来。因此试题的设计要直面学生“思”和“想”的过程，考查学生思考的方式和路径，不断帮助学生建构联系，让学生从经历到经验，从经验到能力，找到数学理解的“根”。

例8：比较图5中的两根铁丝，选项（ ）是正确的。

图5

A.第①根长 B.第②根长

C.一样长 D.无法判定哪根长

【分析与思考】错落放置的两条线段光凭眼睛观察，很难比较出结果。只有建立在测量基础上的线段，才能比出长短。此题的设计，评估的是学生的测量意识、对线段端点的价值认识，观察、分析、推理能力的培养都融合其中。

例9：用小棒按照如下方式摆图形(如图6）。

图6

（1）摆1个四边形需要4根小棒，摆2个四边形需要（ ）根小棒，摆3个四边形需要（ ）根小棒，摆10个四边形需要（ ）根小棒。

（2）如果想摆n个四边形，需要（ ）根小棒。

（3）有169根小棒，可以摆（ ）个这样的四边形。

【分析与思考】第（1）题前两问简单明确的指示性操作，学生通过看与数就能轻易得出答案；第（3）题看与数已不能够解决问题，逼迫学生进行数学思考。当学生构建出小棒的个数与四边形的个数间的关系式时，其实就是把数学问题转化为代数问题，把代数问题转化为方程问题来解决。

4.从“学科”走向“实践”。

真实的情境强调的不只是一系列技能，还是一种观察世界和从事实践的思想及观念的样态，最终强调的是学生对数学文化的感悟。

例10：某保温桶的水大约可以装满15个热水瓶，这个保温桶大约能装（ ）水。

A.30毫升 B.300毫升 C.30升 D.300升

【分析与思考】此题不仅仅考查学生对容积单位“升”和“毫升”的理解，而且考查学生对具体情境中的数量关系的分析推理能力。对这个保温桶容积的认知，必须建立在对一个热水瓶容积的认知（经验）基础上。

例11：珍妮和卡利一起去买鞋。珍妮选了两双鞋，一双标价为110元，另一双为100元；卡利选了一双鞋，标价160元。她们付钱时，营业员告诉她们商店有促销活动，只需付2双的钱就可以拿到3双鞋 （3双中最便宜的一双可以免费得到）。参加促销活动后，珍妮和卡利各需付出多少元？给出2种不同的方案，并说明哪种方案更公平。

【分析与思考】本题创设了学生比较熟悉的商场购物促销活动的问题情境。情境的真实性增强了试题的效度，强调的是决策方案、说理过程以及社会协商性。学生在解决问题时，内化了试题的各种要素和本质，形成了一种用数学的思维方式和眼光。问题的开放性拓宽了学生思考的空间，便于学生进行个性化的表达。学生在解决问题的同时，会权衡不同方案，产生新的想法。此题答案至少 5 种（卡利付款数）：（1）123.33 元（所有鞋子价格和的）；（2）110 元（一共节省 100元，两人平均省下 50 元）；（3）126.67 元（一共节省 100 元，平均每双鞋省下 33.33 元）；（4）135 元（承担参加活动后总钱数的一半）；（5）116.76元（比例推理：卡利的鞋价占3双鞋总价的比率）。

总之，基于数学理解的命题应直指内隐素养，直通生活实践，直面思考过程，强调知识间的联系。这是对传统试题浅表化、形式化、机械化、功利化的祛弊、解弊的过程，期望这样的命题能更好地诊断学生的数学素养落实情况，从而改进日常的数学教学，促进学生数学核心素养的发展。