装载机动臂焊后变形矫正研究

王国安 ，高 超

（1.广西科技大学 机械工程学院，广西 柳州545006；2.广西柳工机械股份有限公司，广西 柳州545007）

动臂是轮式装载机的主要结构件，由连接横梁和两块动臂板焊接而成，连接装载机的车身和铲斗，在装载和挖掘承受工作载荷，在挖掘插入物料时所受的冲击载荷最大，因此，动臂的质量关系装载机的整体性能[1]。动臂板一般为50～60 mm厚的钢板，连接横梁为20 mm厚的椭圆筒型，要求开档尺寸误差在±2 mm以内，两车架端圆孔端面和两铲斗端车架端面关于动臂中心线对称（如图1所示）。在焊接时动臂板内测受热，焊缝集中在椭圆筒周围，受热不均引起动臂板两端的角变形和扭曲变形，使动臂板的开档尺寸和对称度发生变化，严重影响下道机加工工序的效率和成本[2]。为了提供动臂的加工质量和效率，需要对动臂进行焊后变形矫正。

图1 装载机动臂结构及尺寸要求

动臂焊后变形矫正通过夹紧动臂横梁连接处，对需要矫正的动臂板端由液压缸施加载荷使动臂发生塑性变形，以抵消动臂焊后的变形量[3]。在矫正中矫正距离直接关系到卸载后动臂的偏差量，目前矫正中只能依赖经验数据，在多次矫正中不断减小焊后变形量[4]。通过对矫正过程的研究可以为动臂变形矫正提供理论支撑，为探讨如何获得和合适的矫正距离提供支持，指导矫正工艺改进。

1 动臂矫正过程的位置变化

动臂矫正过程中动臂有4个位置变化，与之相应的有4个变形量（如图2所示），动臂板焊接由于残余应力发生变形，偏离标准位置，通过加载矫正使动臂变形至加载矫正位置，完成矫正后卸载动臂发生回弹，最终动臂处在卸载后的位置，由于矫正距离不易控制和预测，大部分矫正后动臂很难回到标准位置。动臂矫正即是不断重复上述过程直到动臂矫正端回到标准位置。

根据动臂板到标准位置的在矫正中距离变化，有4个变形量，分别为矫正距离、矫正前偏差量、矫正后偏差量和回弹量，分别用 y1、y2、y3、y4表示，则有：

矫正前偏差量可以在矫正前获得，如果能获得矫正距离和回弹量的关系，就可以在矫正中通过控制矫正距离使矫正后偏差量接近0.

2 矫正过程载荷和变形量的关系

动臂板矫正时固定横梁连接处，在矫正端施加载荷，可将矫正过程视为悬臂梁受集中载荷的模型（如图3所示），各变形量即为自由端挠度变化量。

图3 悬臂梁受集中载荷模型

动臂矫正的过程实质是机械加载使动臂发生塑性变形来抵消焊接产生的塑性变形，因而在矫正中必须使动臂板发生塑性变形。由内力平衡可知，动臂板自由端受集中载荷时动臂板各处弯矩分布为：

当x=0时，M=-LP，弯矩最大。因此动臂板发生塑性变形是从横梁夹紧处开始，当横梁截面应力达到材料的弹性极时，由截面平衡方程可得此时弹性极限弯矩Me：

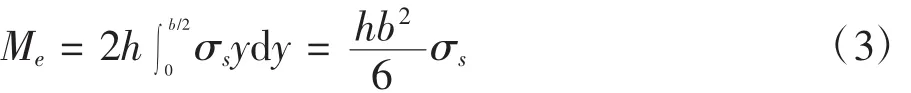
其中σs为屈服极限。

则载荷为：

当载荷P＜Pe时，动臂板只发生弹性变形，卸载后动臂板会回弹到加载前的位置，此时回弹量等于矫正距离，矫正后偏差量等于矫正前偏差量，毫无矫正效果。只发生弹性变形时，变形量符合材料力学中的悬臂梁挠曲方程。

其中E为材料的弹性模量，I为惯性矩，将P=Pe代入可得：

其中ymin为最小矫正距离，Pe为最小的矫正载荷。当小于此矫正距离时矫正无效。

当载荷P＞Pe时，靠近夹紧位置横截面的最上层开始产生塑性变形，继续增加载荷塑性区域变大，塑性变形区的应力为屈服应力σs，弹性区域应力小于屈服应力，越靠近截面中心位置应力越小（如图4所示）。当截面任意层应力都为屈服应力时，此时弯矩达到了塑性极限弯矩，夹紧处截面全部分为塑性变形，形成塑性铰[5]。

图4 塑性变形截面应力分布

动臂矫正中施加载荷不可超过pmax,否则零件将会报废。由式（4）和式（7）可知需求载荷范围为：

此时载荷为：

悬臂梁受集中载荷自由端弯曲变形解是一个复杂的问题，自由端的变形转角和变形量求解方程是一个含有椭圆积分的超越方程，求解非常不便[6]。文献[7]中提出一种使用伽辽金法推导出精度较高的近似解法，其方程为：

卸载时载荷等于加载结束时载荷，卸载后材料发生不可逆的塑性变形，回弹服从弹性变形规律，弯矩改变量和曲率改变量成正比关系。最大回弹量可有最小势能原理求得，动臂回弹势能方程为：

其中A（K）动臂应变能密度，M为弯矩，K为变形的曲率。为当载荷为极限载荷pmax时弯矩分布为：

设最大回弹量为：

曲率 K（x）=-A-Bx，将 M（x）、K（x）代入式（9）并对式（11）求A、B的极值，得极限载荷下回弹量方程：

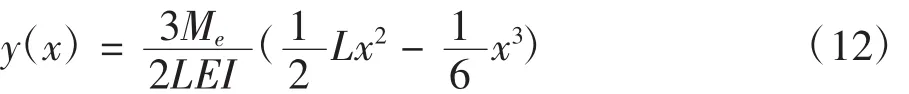
结合式（6）可知，动臂矫正时回弹量范围为：

由于回弹符合弹性规律，则有：

其中P′为卸载载荷，yi为任意弹性阶段变形量，Pi为对应的载荷值，由式（14）和式（1）可得：

由于发生塑性变形时挠度变化和载荷关系比较复杂，矫正时，矫正距离可设为：

又因为卸载载荷等于加载时载荷，将P′=P和式（16）代入式（15）可得：

以y1为因变量则存在：

当矫正前偏差较小时，动臂变形量为y2时，动臂处于弹性变形阶段，令yi＝y2，则存在：

由上式可知动臂矫正距离与矫正前偏差量，矫正后偏差量，矫正至标准位置时载荷有关，那么在矫正中加入位移传感器和压力传感器来检测记录矫正中的数据，将这些数据作为样本，通过决策树、神经网络等机器学习方法训练学习样本，就能在矫正中获得合适的矫正距离。

3 结束语

本文通过分析机械液压矫正动臂焊后变形过程，将动臂矫正视作悬臂梁自由端受集中载荷的模型，经过分析变形和载荷的关系，得到了矫正时需求载荷的变化范围、最小的矫正距离、回弹量变化范围，为设计动臂矫正工装提供参考，通过分析矫正距离、矫正载荷、矫正前偏差和矫正后偏差的关系，为今后通过机器学习等决策矫正距离的采样提供支持。