大型模锻压机驱动系统建模及动态特性研究
2018-08-04熊志宏曾珍珍
范 彬,熊志宏,曾珍珍
(湖南城市学院机电工程学院,湖南 益阳413000)
现代工业的迅猛发展,使得大型模锻液压机在空天运载、船舶动力、石油化工等行业发挥的作用愈发重要。因此不仅需要制造更多高性能大型模锻压机,也需要对现有已投入生产的大型模锻压机进行分析以进一步提高工作能力。低速稳定性是衡量压机性能的一个重要指标[1],在压机运行过程中,泄漏、油液体积压缩、非线性摩擦、粘性阻尼系数等这些因素对其低速稳定性的影响最大[2],而且这些因素之间又相互影响。因此,如何获得这些参数对压机低速稳定性的影响规律,来改善液压机系统的动态特性,从而提高整个压机系统的性能,都具有重要意义[3]。本文围绕大型模锻压机驱动系统建模、参数辨识和低速稳定性影响因素分析展开研究,分析了大型模锻压机驱动系统低速动态特性。建立了压机驱动系统仿真模型,分析了摩擦、泄漏、油液体积模量对低速稳定性的影响。
1 驱动系统建模
4000T等温模锻压机进行锻压工艺时,采用三缸合流驱动。回油路上设置系统背压,增大系统的阻尼力,不考虑系统的偏载和不同步,系统的低速驱动原理图可进行简化等效为图1所示。图中,主驱动缸4的有效面积为3个主驱动缸的有效面积相同,回程缸6的有效面积与4个回程缸的有效面积相同,油液管道的管径和长度分别与实际的管道等效。
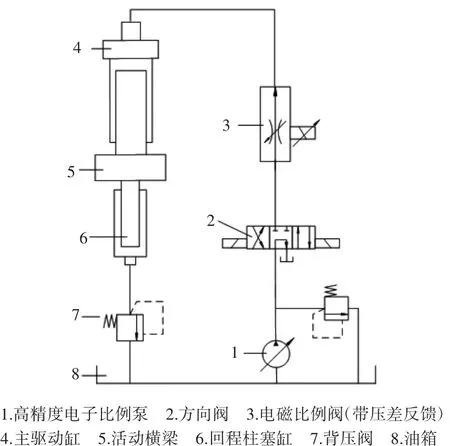
图1 4000T模锻压机低速驱动系统原理图
1.1 活动横梁力学模型
大型模锻压机工作时,一般将锻压机的活动横梁看作刚体[4],以活动横梁(见图1中部件5)为分析对象,所受的力如图2所示。
其受力平衡方程为:


图2 活动横梁受力分析图
其中:M 为活动横梁质量(kg);Fr为摩擦力;x为横梁位移;F1为主缸驱动力;F2为回程缸背压力;Fb为油液粘性阻尼力;FL为锻件的变形抗力。
1.2 电磁比例阀建模
电磁比例阀不考虑运动产生的摩擦和阀芯重量对系统的影响,此时流量方程为:

其中:CdT为流量系数;WT为面积梯度(m);xT为阀开口大小;ks为弹簧刚度(N/m);xc为弹簧初始压缩量(m);ρ为油液密度(kg/m3);AR为阀芯有效作用面积(m2);
电磁比例阀开口大小xT与输入电压成正比,因此有:

式中:u为输入电压值(V);KL为电磁比例阀的补偿系数;Kv为比例阀增益。
1.3 主驱动缸建模
主驱动缸建模时,采用三缸合流的驱动方式。在进行等温锻造工艺时,系统工作在低速条件下,所需的供油流量是非常微小的,对阀的精度要求非常高。传统的方法是单缸单泵分流独立驱动,低速运动时单缸所需的流量更加微小,从硬件上很难有额定流量如此小的阀,即使有,不仅成本极高,且大多工作在非线性区,不便于控制,导致低速稳定性变差;另外,单缸单泵分流独立驱动增大了流量阀自身非线性对系统低速性能影响的比重。采用三缸合流驱动技术,可以降低系统低速驱动对流量精度的要求,同时可以起到降低系统偏载的作用。根据可压缩流体的连续性方程,有:
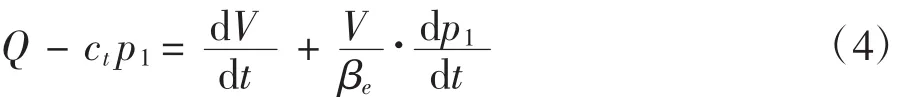
式中:ct为泄漏系数 (m5/N×s);V 为油腔体积(m3);βe为油液体积弹性模量(N/m2)。
其中:

式中:V0为3缸进油腔初始容积之和(m3);A为3缸有效作用面积之和(m2);x为柱塞位移(m)。
由式(4),(5)可得:

2 系统动态特性分析
液压机驱动系统的动态特性是各元件动态特性的综合效应的结果,且包含众多非线性影响因素,常采用变步长R unge-Kutta法求解微分方程中的非线性问题。为此作者利用R unge-Kutta法结合MATLAB软件对液压机驱动系统数学模型进行动态仿真。设定速度1×10-4m/s,研究各个参数对大型等温模锻系统动态特性的不同影响。其仿真结果如图3~图5所示。
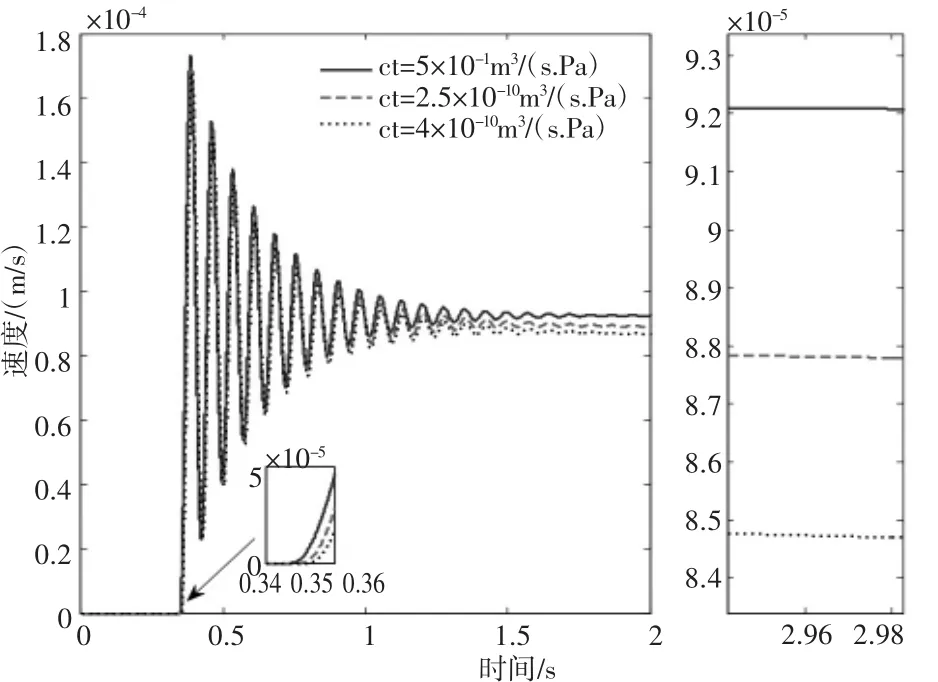
图3 不同泄漏下的速度响应仿真图

图4 不同系统粘度阻尼系数下的速度响应仿真图

图5 不同油液体积弹性模量下速度响应仿真图
2.1 泄漏系数ct的影响
在压机运行过程中,柱塞缸和比例阀的泄漏是影响压机系统低速稳定性的主要因素之一。图3为取不同的泄漏系数时压机系统的速度仿真图。当泄漏系数分别为5×10-11m3(/s×Pa)、2.5×10-10m3(/s×Pa)和4×10-10m3(/s×Pa),压机系统的速度速度响应延时分别为0.3478 s、0.3507 s和0.3528 s,速度收敛值分别为9.2×10-5m/s、8.65×10-5m/s和8.26×10-5m/s.从图3上可知,随着泄漏系数的增大,柱塞缸和比例阀的泄漏量也随着增大,而流量随之减少。此时,由于泄露量的增大、流量的减少降低了压机系统的能量传递效率,从而导致压机系统的低速稳定性变差。
2.2 粘性阻尼系数的影响
在压机运行过程中,压机的粘性阻尼系数是影响系统低速稳定性的一个重要参数,它主要与油液温度和运动粘度有关。图4为取不同的粘性阻尼系数时压机系统的速度仿真图。分别取系统粘度阻尼系数B为9.06×105N(/m/s)、1.206×106N(/m/s)和1.806×106N(/m/s)作仿真对比。由图4可知,随着B的增大,可以看出速度响应延时几乎不变,但是速度超调量Mp却逐渐降低,分别为88.04%、83.7%和75.54%,速度的调整时间ts逐渐减短,分别为0.784 2 s、0.564 4 s和0.346 1 s.这是因为随着粘性阻尼系数的增大会导致系统阻尼增大,从而使系统的能量损失增大,但是这对系统的低速稳定性是有好处的。因此,在选择系统的粘性阻尼系数时,必须在综合考虑系统的稳定性和能量利用率的基础上,通过优化设计来确定其最佳值。
2.3 油液体积弹性模量的影响
在压机运行过程中,液压油的体积弹性模量是液压机系统低速稳定性的的主要参数之一,它与油液温度、油压和空气含量有着密切的关系。图5为取不同的油液体积弹性模量时压机系统的速度仿真图。当取为0.7×109N/m2,系统的速度响应延时为0.347 8 s,再经过0.784 2 s的达到稳定速度,为9.2×10-5m/s.当取体积弹性模量βe为1.4×109N/m2和2.1×109N/m2时,速度响应延时分别为0.195 7 s和0.1304 s,调整时间分别为ts=0.773 3 s和ts=0.751 5 s,稳定速度分别为9.35×10-5m/s和9.83×10-5m/s,速度的超调量均逐渐增大。这是因为随着温度和油压的升高,油液的体积弹性模量也会随之增大[5]。
3 结语
本文采用解析法建立大型模锻压机驱动系统的仿真模型,重点分析了油液体积弹性模量、泄漏系数、粘性阻尼系数对系统极低速稳定性的影响,从而得到了这些参数对锻压机的影响规律,并提出了解决办法,来提高大型模锻压机驱动系统的低速稳定性。
