改进细菌觅食算法在PID参数整定中的应用*

李晓含, 王联国

(1.甘肃农业大学 机电工程学院,甘肃 兰州 730070；2.甘肃农业大学 信息科学技术学院,甘肃 兰州 730070)

0 引 言

细菌觅食优化(bacterial foraging optimization,BFO)算法具有鲁棒性强、易于实现、可并行处理与全局搜索的特点[1],在许多领域已广泛应用,但其存在着收敛速度慢,极易陷入局部最优缺点。文献[2]将粒子群优化(particle swarm optimization,PSO)与SA结合作为一个PSO-SA变异因子,改善细菌的交流能力；文献[3,4]将BFO与PSO结合,提高算法的寻优机制；文献[5]将遗传算法(genetic algorithm,GA)与BFO算法混合,增大其搜索能力,提出了电力系统无功优化的遗传—细菌觅食优化混合算法(GA-BFO),文献[6]在细菌觅食算法趋向操作中,引入碰壁策略优化初始位置,提高收敛速度；文献[7]提出了定义进化域的方法确定细菌前进方向,解决离散域问题存在的缺陷；文献[8]提出了自适应步长与概率,解决陷入局部最优问题,并应用于图像分割中；文献[9]将粒子群与细菌觅食算法结合,提高了搜索能力,应用于三电平逆变器中；文献[10]将改进细菌觅食算法应用于软测量建模中。

本文对细菌觅食算法的趋化操作与迁移操作改进,以加快细菌觅食的搜索速度与寻优精度,并采用测试函数及比例—积分—微分(proportion integration differentiation,PID)参数整定的仿真试验检验效果及可行性。

1 基本细菌觅食算法不足

标准细菌觅食算法包括：趋化、群聚、复制和迁徙，算法存在的问题为：个体间交流信息较少，影响收敛速度。

2 改进的细菌觅食算法

2.1 趋化改进

将粒子群优化算法运用于细菌觅食算法趋化操作中,加大个体间的信息交流,提高收敛速度与精度,则细菌觅食算法在趋化操作时任意方向翻转移动更新公式为[11]

ψ(j+1)=w×ψ(j)+c1r1(pbest-pcurrent)+

c2r2(gbest-pcurrent)

(1)

权重w在粒子群算法用来平衡算法的全局寻优与局部寻优,当取值大时利于全局寻优,但难以得到精确值；当取值小时利于局部寻优,但易陷入局部极值点。故采用自适应调节方法,即每个粒子依据自身当前适应值来调节变化,即

(2)

式中wmin,wmax[12]分别为最大值与最小值；fi为当前粒子适应值；fav,fmin分别为平均值与最小值。

2.2 迁徙改进

采用自身适应度来调节迁移方式,在迁徙操作时,先对个体适应度值比较,得出最优2个个体不进行迁徙,最差的3个个体直接迁徙,中间则延续一般方式,根据适应度进行动态调整按照式(3)对迁徙概率优化

(3)

式中Pmin与Pmax为迁徙概率最大值与最小值；Jmax与Ji为最好健康适应度值与当前i健康适应度值。

当进化较快时,以低概率进行迁徙,可以保持当前有利信息；当较慢时,易陷入局部最优,需要较高概率迁徙,以跳出局部最优。

2.3 算法主要流程

1)初始化各参数,s,p,Nc,Ned,Nre,Sr,Ped,c1,c2,r1,r2等,其中,s为细菌总个数,p为搜索空间维度,Nc为趋向操作次数,Ned为迁徙操作数,Nre为复制操作数,Sr为细菌总数1/2,Ped为迁徙概率,c1,c2,r1,r2为PSO随机参数。

2)计算细菌适应度值,将细菌目前适应度值作为个体细菌历史最好位置,所有细菌适应度最好值作为全局最优。

3)利用新公式更新细菌方向与位置。

4)在返回步骤(2)重新计算适应度值,与历史最好位置比较,如果更优,将取代历史最好值。再将结果与群体最优比较,若更优,将其作为全局最优。

5)复制循环,计算适应度值,满足条件个体复制新个体取代另一半不满足条件个体。

6)迁徙循环,复制完后生成一个随机概率,与动态迁徙概率比较,若小于概率,进行迁徙。

7)输出结果。

3 测试函数

3.1 仿真设计

本文采用6个常见的标准非线性测试函数对细菌觅食算法及改进细菌觅食算法进行测试对比,测试函数最优值一般都难获得,且随着维度增加,优化难度随之急剧加大,测试函数如下：

1)Sphere函数(x∈[-5.12,5.12],最优解为0)

(4)

2)Quartic函数(x∈[-1.28,1.28],最优解为0)

(5)

3)Griewank函数(x∈[-600,600],最优解为0)

(6)

4)Schewefel函数(x∈[-500,500]最优解-12 569.5)

(7)

5)Rastrigrin函数(x∈[-5.12,5.12],最优解为0)

(8)

6)Ackley函数(x∈[-32,32],最优解为0)

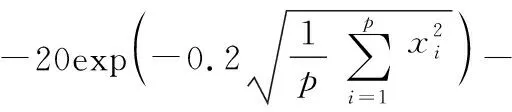
3.2 仿真结果与分析

本文细菌觅食算法参数选取值参考文献[13],设置测试函数维度为30；细菌种群规模为30；Nc为40；游动次数为5次；复制次数为5次；迁徙次数为5次,仿真结果表1。

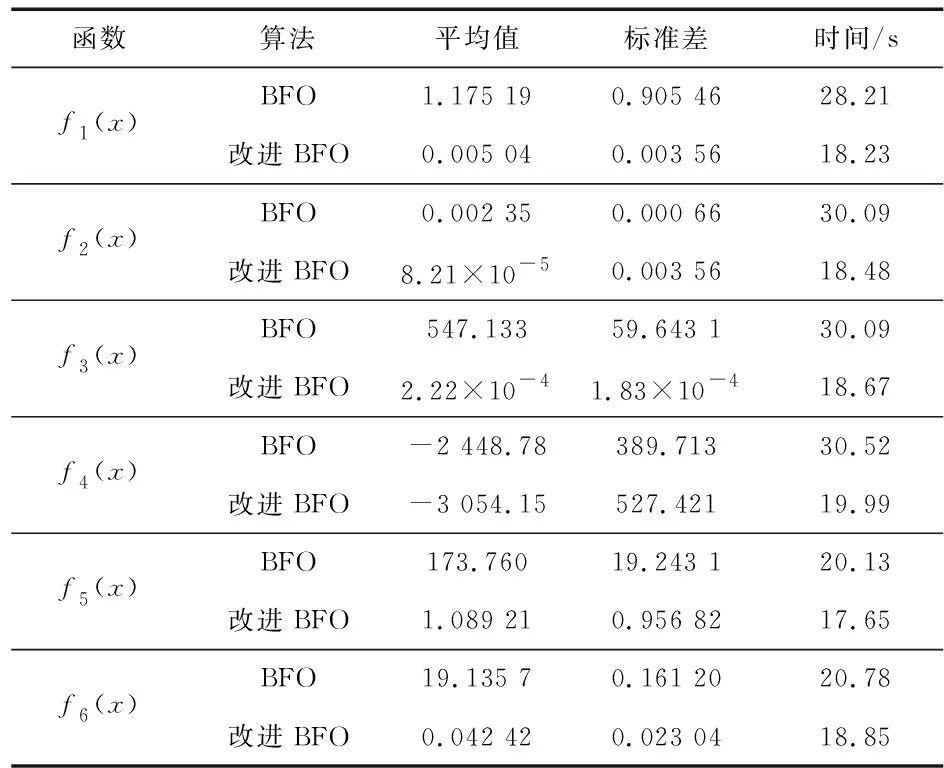
表1 固定迭代次数下寻优结果(四舍五入值)

表1为原始与改进细菌觅食算法在测试每个函数时,独立运行20次结果。由平均值可以看出：较难获得全局最优解的Rastrigrin函数与函数Ackley函数提高了寻优精度,获得较优的值；Griewank函数寻优精度提高约有5个数量级；其他测试函数也获得较好的寻优解；说明改进细菌觅食算法对易陷入局部最优特点得到改善。从运行时间列可以看到,改进细菌觅食算法运行时间较短,说明改进后的搜索速度要快些。因此,改进细菌觅食算法在寻优进度和搜索速度上均得到一定改善,验证了算法的可行性与有效性。

4 应用实例

为了达到更好的控制效果,本文在PID控制器参数优化设计中,采用细菌觅食优化算法优化调整PID的ki,kp,kd3个参数,实现输入与输出的实时跟踪。细菌觅食智能算法PID控制结构如图1所示。

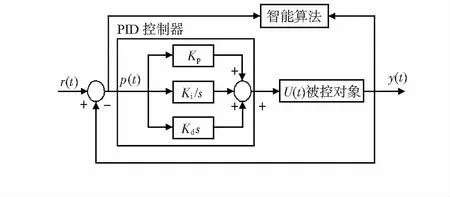
图1 智能控制

图1中,r(t)为系统输入函数；y(t)为系输出函数；U(t)为控制器输出。

4.1 被控对性

本文采用一阶系统与一阶惯性延迟两个基本模型,进行PID控制仿真实验,其被控对性为

(9)

4.2 目标函数

评价误差性能选用时间误差绝对积分(integral of time multiplied absolute value of error,ITAE)作为目标函数,其公式为

(10)

4.3 编 码

在整定中,PID控制器参数设置为细菌在空间中位置,在细菌觅食算法中,v表示算法的维度,则用一组参数向量Xi=(x1,x2,…,xv)表示细菌所在的位置,ki,kp,kd为细菌觅食算法中的优化参数,细菌觅食算法的位置则定义为 (ki,kp,kd)。在参数整定中,将个体值依次赋给参数ki,kp,kd,然后到运行控制系统Simulink模型,得到对应的性能指标,该指标传递到细菌觅食算法中作为适应度值,进行一步对比优化,最后退出算法[14]。PID参数整定流程如图2。

4.4 仿真结果与分析

采用MATLAB软件进行仿真,对PID参数整定,用改进细菌觅食进行择优,并将改进结果与原始算法在性能指标对比。

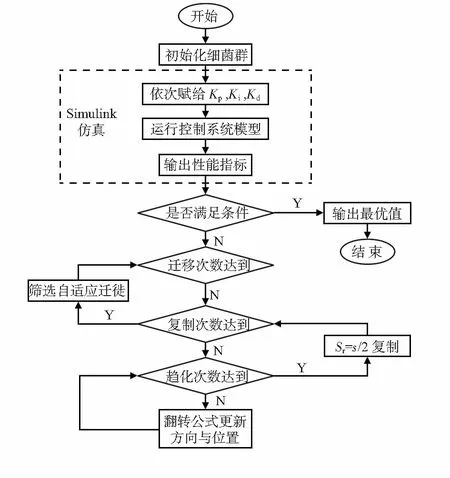
图2 参数整定运行

表2所示为控制性能指标,性能指标ITAE取值越小,其超调量越小,则系统的稳定性越好;反之,系统稳定性较差。在性能评价指标ITAE中,改进细菌觅食算法中ITAE获得值更小,则改进细菌觅食算法整定参数用于系统获得更稳定的效果。

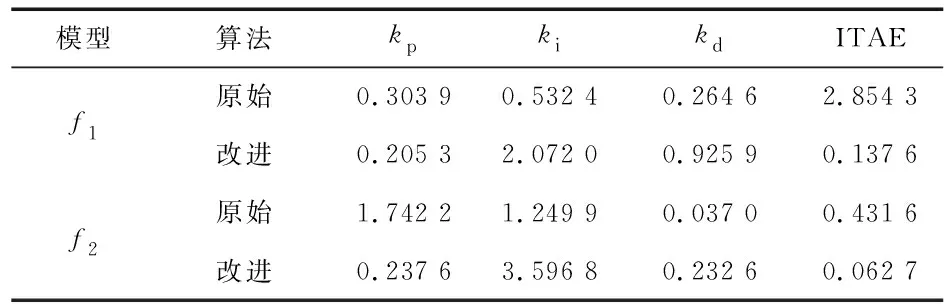
表2 控制性能指标

图3为原始BFO算法与改进BFO算法得到参数代入系统中所得到的相应系统阶跃响应曲线。上升时间为第一次达到稳定时间,从图3可知：改进后BFO算法与原始BFO算法相比,其上升时间较快；而峰值时间与调整时间的速度均用了评价系统的响应速度,从图3可知到达峰值时间与调整时间都较快,具有更快的反应速度。

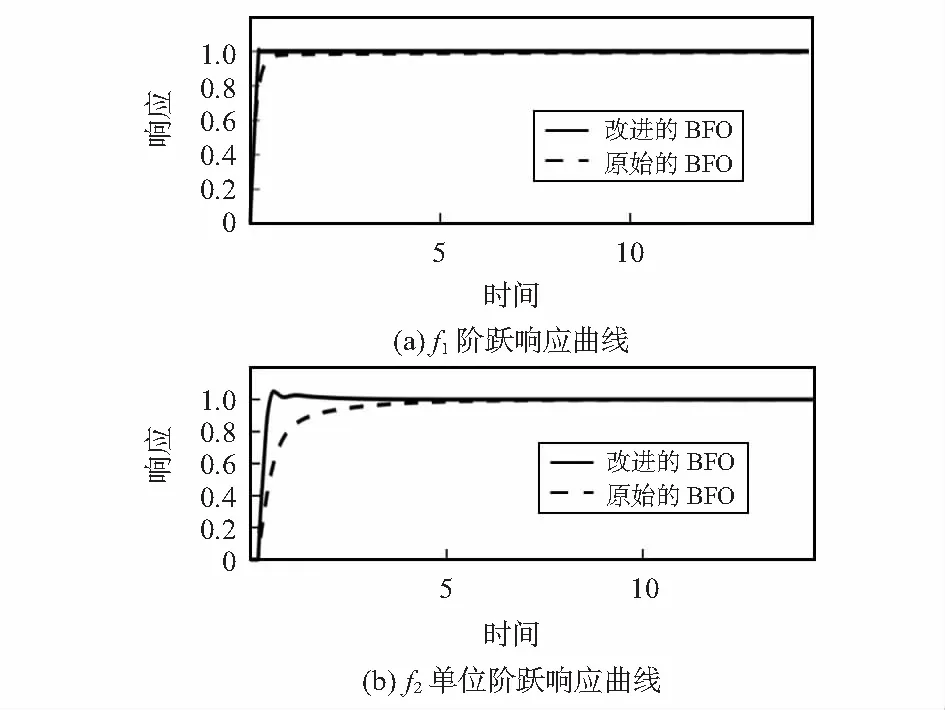
图3 对象阶跃响应曲线

图4为BFO算法和改进BFO算法优化的ITAE变化曲线。从图4中可以看出,改进BFO算法在迭代120次左右收敛,原始细菌觅食算法在280次左右得到收敛,得出改进算法收敛速度更好些,可以得出改进算法有效性及适用性。

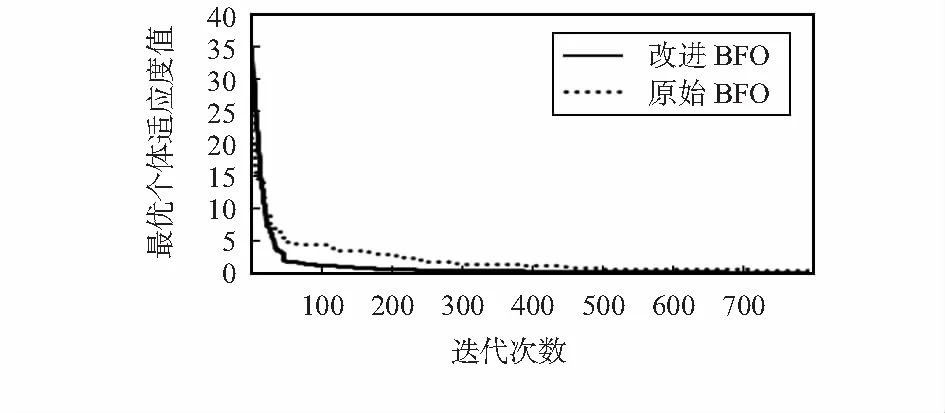
图4 2算法的迭代曲线

可知,改进细菌觅食算法在PID整定应用中,其阶跃响应的超调量减少,收敛速度与反应时间得到提升,系统响应速度快,控制品质得到了很大改善。

5 结 论

针对细菌觅食算法存在收敛速度不够快,易陷入局部极值等不足,提出了一种细菌觅食改进算法,对趋化操作与迁徙操作进行改进。用标准测试函数和PID参数整定实验,对改进细菌觅食算法进行测试,结果表明该改进方法可以提高寻优精度与搜索速度。