WSNs中基于RSS的协作式节点定位算法

马永光， 王 朔， 邢 建， 石 乐

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引 言

近年来，无线传感器网络[1](wireless sensor networks,WSNs)节点定位算法可归为两类：基于测距(range-based)的方法与非测距(range-free)的方法。Range-Based方法通过测量绝对距离或方位角度等信息确定节点位置，定位精度取决于测量的准确性。在基于接收信号强度(received signal strength,RSS)的定位方法中，节点根据无线信道的路径损耗模型，利用RSS值估计距离。RSS值易受环境噪声影响，影响测距的准确性[2,3]。在现有的基于RSS的定位方法[4,5]中，常常忽略噪声对RSS的影响，定位精度差强人意。

诸多定位算法又可以分为非协作式定位[2,6,7]与协作式定位[3,8]。前者仅仅利用未知节点与每个锚节点间的测量距离，逐个确定每个未知节点的位置信息；后者则利用网络中包括未知节点在内的所有节点间的测距数据，同时确定全部未知节点的位置。受节点成本与监测环境复杂程度的制约，网络中锚节点的数量十分有限，协作式定位往往能够实现更高的定位精度。

本文在充分考虑了噪声因素的基础上，将加权最小二乘法(weighted least squares，WLS)与多维标度分析法(multidimensional scaling，MDS)相结合，提出了一种新的基于RSS的协作式定位算法—WLS—MDS。

1 RSS测距的基本原理

1.1 路径损耗模型

通过在不同环境下的反复测量与理论分析，通信节点间的欧氏距离d与接收信号强度P满足Log-Normal Shadowing Path Loss模型[9]

P=P0-10nplgd+ω

(1)

式中P0为距离信号源d0;d0为参考距离(通常取d0=1 m)处的接收信号强度;nP为路径损耗指数;ω为具有方差

σ2的零均值高斯白噪声。在某一特定的环境下σ2是一个与距离无关的常数。

1.2 dm无偏估计

为避免在噪声强度较大的环境下常规dm简化模型引起更大的测距误差，导致定位精度的恶化，本文在已知σ的情况下，采用文献[10]中提出的dm的无偏估计量m构造距离矩阵

(2)

令Y=lnm，发现Y满足均值为方差为λ2σ2的正态分布,则m服从对数正态分布,其数学期望与方差为

E(m)=dm,var(m)=d2m(eλ2σ2-1)

(3)

2 MDS的基本原理

WSNs由分布在二维空间中的M+N个传感器节点组成，节点位置信息由平面直角坐标系中的坐标值唯一确定，其中,第i个节点的坐标向量xi=[xiyi]T。不失一般性，假设前M个节点为位置已知的锚节点，后N个节点为需要定位的未知节点。对网络中每两个节点所组成的节点对作如下划分

(4)

式中Θ1为每两个锚节点组成的节点对的集合，Θ2为每两个未知节点组成的节点对的集合，Θ3为每个锚节点与每个未知节点组成的节点对的集合。由锚节点与未知节点的坐标所组成的坐标矩阵分别为Xa=[x1x2…xM]，Xs=[xM+1xM+2…xM+N]，网络中所有节点的坐标矩阵为X=[XaXs]。根据MDS的基本原理，X的中心化内积矩阵

B=JXTXJ=-0.5JDJ

(5)

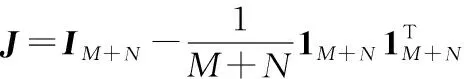
D=

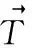
(6)

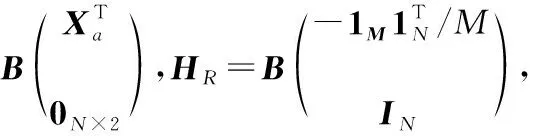
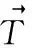
3 WLS-MDS定位算法

在实际的应用环境中，由于高斯白噪声的存在，Θ2与Θ3中包含的节点对之间的实际距离无法精确测量，只能根据d2的估计值构造矩阵D，此时X的中心化内积矩阵近似的表示为

(7)

式中

根据前文的推导结果，这里用dm的无偏估计来构造矩阵D。令m=2，则

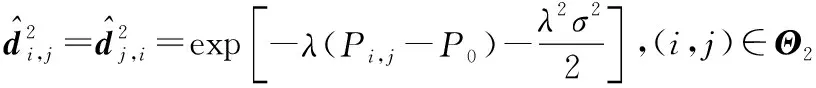
在考虑噪声的情况下，将式(6)改写成

(8)

对式(8)等号两侧同时进行向量化操作

(9)

式中hR，ξ和xs分别为R，Ξ和Xs的向量化运算结果，⊗HL。

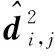
(10)

式中W为权值矩阵，根据文献[8]，W的最佳取值为马尔可夫估计

W=[cov(ξ)]

(11)

根据式(8)与式(10)

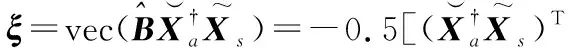
(12)

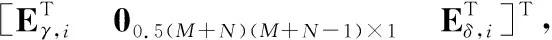
i=1,…,M+N

(13)

式中Eγ,i=[eα(i,1)eα(i,2)…eα(i,i-1)]T,i=2,…,M+N;Eδ,i=[eα(i+1,i)eα(i+2,i)…eα(M+N,i)]T,i=1,…,M+N-1;α(x,y)=0.5[2y(M+N)-2(M+N)-y2-y]+x。

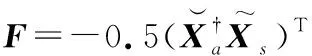
W=(FΨCdΨTFT)

(14)

式中Cd为d的协方差矩阵，由于节点间RSS的测量相互独立，Cd为对角矩阵。并且根据式(3)，Cd的第β(i,j)个对角线元素

β(i,j)=(i-1)(M+N)-0.5i(i-1)+j-i

(15)

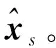
4 仿真实验与结果分析

在MATLAB 7.0上对本文提出的WLS-MDS算法进行仿真实验，并将实验结果与MDS以及文献[4]提出的线性最小二乘(linear least square,LLS)定位算法进行对比。本文以所有未知节点定位误差的平均值作为衡量定位精度的标准

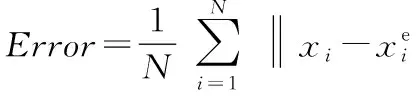
式中xr为未知节点的真实坐标;xe为未知节点坐标的估计值。

图1为某一次执行WLS-MDS算法的定位结果。

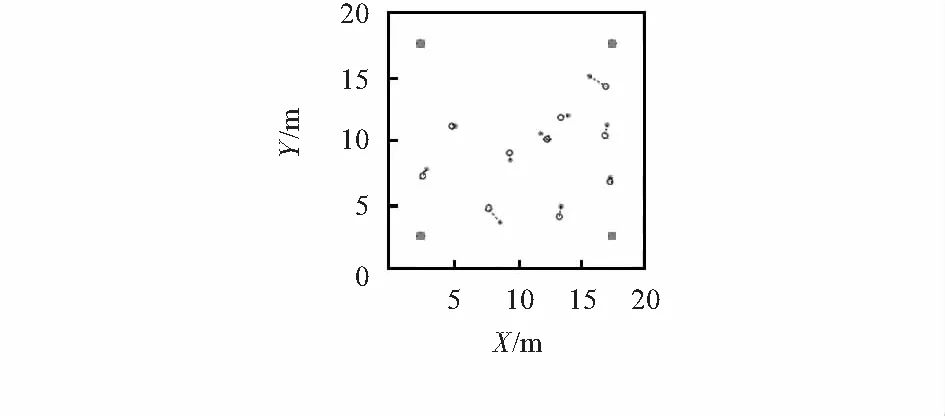
图1 WLS-MDS算法的定位结果

如上图所示，无线网络由4个锚节点与10个未知节点组成，锚节点分别固定在坐标值为(2.5,2.5)m,(2.5,17.5)m,(17.5,2.5)m,(17.5,17.5)m的位置上，未知节点则随机分布在20 m×20 m的矩形区域内。星号表示未知节点的真实位置，圆圈表示WLS-MDS定位算法的计算结果，虚线长度表示该点的定位误差。实验中，取参数为P0=-20 dBm,np=2.5,σ3=4。经计算实验定位误差Error=0.753 0 m。

在参数配置、节点数量及布局与前文一致的情况下，进行2 000次独立重复实验，实验结果统计如图2、图3。

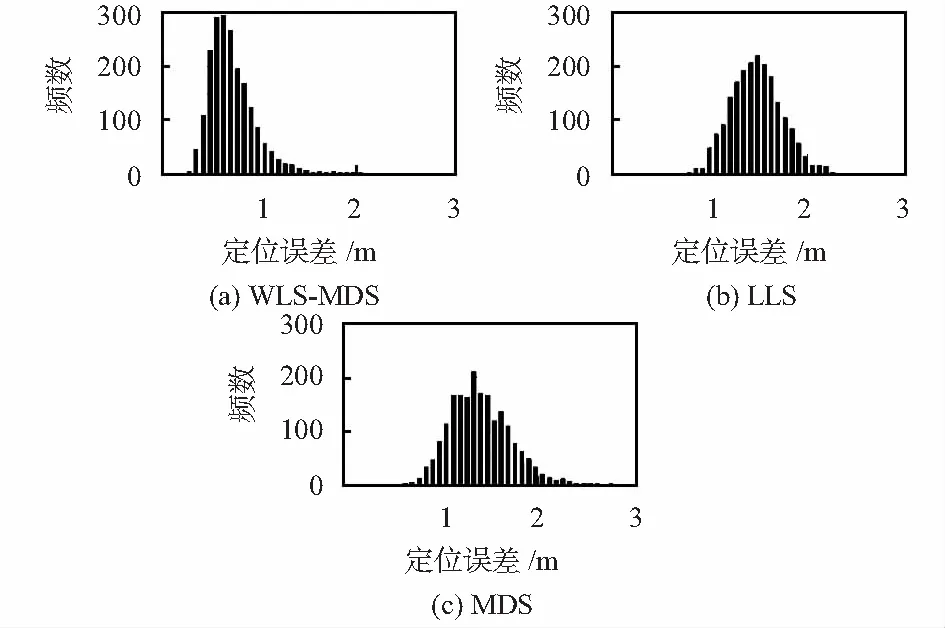
图2 3种算法定位误差频数分布直方图

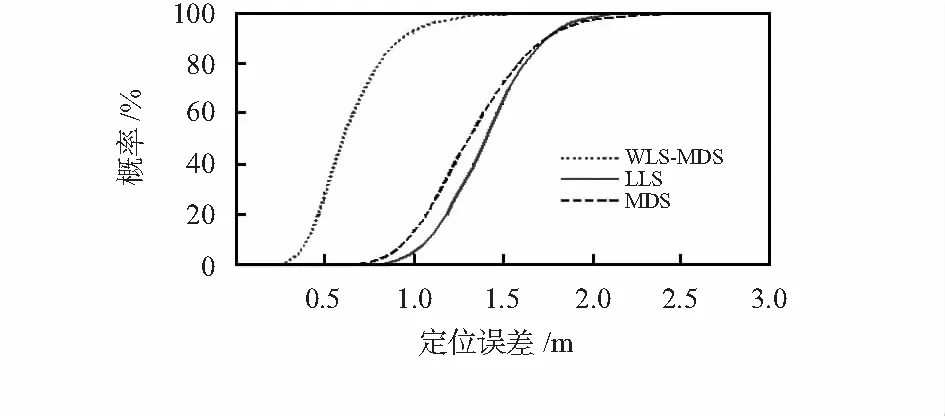
图3 3种算法概率累计曲线

图2为WLS-MDS，LLS，CMDS 3种算法定位误差的频数分布直方图，图3为3者误差的概率累计曲线。在本次实验设置的条件下，WLS-MDS有90 %以上的概率达到Error≤1 m的定位精度，相比另外2种算法和具有显著的优势。

研究环境噪声方差σ2和未知节点数量N对WLS-MDS定位精度的影响，以下实验数据均为独立重复地进行500次仿真实验所得结果的平均值。

1)取参数P0=-20 dBm,np=2.5,σ2=4，锚节点的位置如图1所示，未知节点数目N从1递增至20，3种算法的平均定位误差对比如图4。

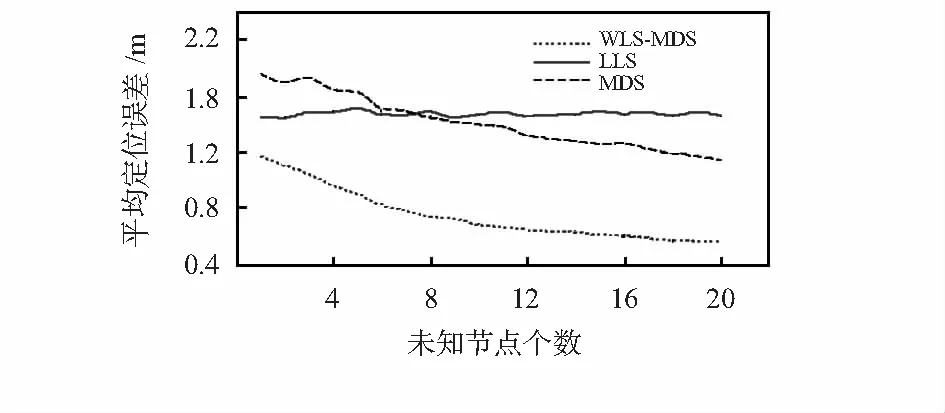
图4 定位误差随N的变化关系

由图4可知，协作式定位算法MDS与WLS-MDS的定位误差会随着网络中节点数量的增加而逐渐减小。而LLS定位算法，作为一种非协作式定位算法，仅仅依靠未知节点与每个锚节点间的测距信息计算节点坐标，其定位精度并不会随着未知节点数量的增加而有所改善。在网络中未知节点数目不同的情况下，本文提出的WLS-MDS定位算法，其定位精度均优于另外2种算法。

2)取参数P0=-20 dBm,nP=2.5，网络中节点分布如图1所示，在噪声方差σ2不同的环境下，对3种算法进行仿真，其结果如图5所示。

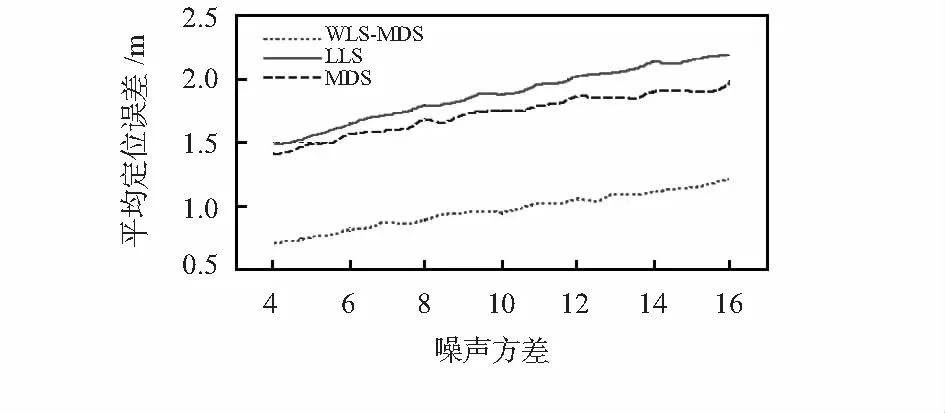
图5 定位误差随σ2的变化关系

随着噪声强度的增加，三者的定位精度均有不同程度的恶化。在不同强度的环境噪声干扰下，WLS-MDS的定位误差均小于其他2种算法。可见，即使在噪声干扰较为严重的环境下，WLS-MDS依然能够达到十分理想的定位精度。

5 结 论

本文提出基于RSS的WLS-MDS定位算法,在已知环境噪声的情况下，利用d2的无偏估计构造距离矩阵，进而计算出未知节点坐标的加权LSE。其本身是一种协作式定位算法，更加适合应用于锚节点数量有限、未知节点数量庞大的WSNs。而且由于该算法结合了WLS与MDS的优点，在定位精度上，较传统的协作式定位算法也具有明显的优势。