基于PCOS-ELM的室内指纹定位算法*
2018-08-03朱顺涛卢先领
朱顺涛, 卢先领
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引 言
近年来,随着无线局域网(wireless local area network,WLAN)的广泛部署以及人们对于室内位置服务的需求与日俱增,WLAN室内定位技术引起了国内外学者的广泛关注[1,2]。根据定位原理的不同,WLAN室内定位技术可分为以下3类:最近接入点(access point,AP)定位、几何计算定位和位置指纹定位[3]。其中,位置指纹定位法凭借定位精度较高、对环境及设备要求低等优点,目前已经成为室内定位技术中的研究热点[4]。文献[5]提出了基于极限学习机(extreme learning machine, ELM)的指纹定位算法,大幅减少了离线阶段的训练时间。文献[6]在ELM中引入了二次锥规划提高定位算法的抗噪能力,缺点是未考虑室内环境的变化;文献[7]对ELM中的隐含层节点进行增量式添加,但由于隐含层节点参数随机分配,定位精度提高不明显。文献[8]提出了一种混沌优化的极限学习机(chaos extreme learning machine,CELM)算法,利用复合混沌优化和混沌尺度变化算法优化ELM的隐含层参数,提高了ELM的泛化性能,但CELM算法容易陷入局部最优,导致定位精度下降。
本文针对现有室内指纹定位算法在定位精度和对环境适应性这两方面缺乏综合考虑的问题,提出了一种基于并行混沌优化的在线连续极限学习机(parallel chaos online sequential-ELM,PCOS-ELM)的定位算法。通过对传统混沌优化二次载波部分进行并行化搜索,避免了在处理高维化问题时陷入局部最优;通过分块矩阵的运算法则对初始化定位模型进行在线连续学习,提高了算法对动态环境的适应性能。
1 CELM定位算法
设有N个位置指纹数据{(xj,tj)}j=1,2,…,N,隐含层节点个数为L,基于ELM的位置估计模型如下
(1)
式中w为输入权值,b为隐含层节点阈值,g(·)为激活函数,β为隐含层节点的输出权值。式(1)可以写成矩阵向量形式
Hβ=T
(2)
(3)
T=[t1,t2,…,tN]T,β=[β1,β2,…,βL]T
(4)
因此,训练ELM定位模型即计算式(2)中隐含层输出权值矩阵β
β=H-1T
(5)
CELM定位算法在ELM基础上,对隐含层节点参数进行组合优化,使得残留误差E最小,即
(6)
式中Y为优化后的隐含层节点参数,包含输入权值w和隐含层节点阈值b;oj为算法对第j个训练数据的输出值。
CELM定位算法主要分为以下3部分:
1)一次载波搜索
采用载波方式将混沌变量引入优化变量,将混沌运动的遍历范围映射到优化变量的取值范围[9]
(7)
minE(Yi),ai≤Yi≤bi
(8)
(9)

2)二次载波搜索
在经过M次一次载波搜索后,若E*保持不变,则按式(10)进行二次载波
(10)
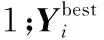
3)计算CELM算法的输出权值和误差
(11)
(12)
若EL小于期望输出误差η,停止循环;否则,L=L+1,转至一次载波部分循环搜索。
2 改进的CELM定位算法
提出的PCOS-ELM定位算法在CELM算法基础上,引入了并行混沌优化和在线连续学习方法,旨在解决以下2个问题:1)CELM算法在求解最优隐含层节点参数时容易陷入局部最优,导致定位精度受到影响;2)基于CELM的定位算法对动态环境的适应性较差。
2.1 PCOS
对CELM二次载波部分进行并行分类讨论,确保优化变量不会全部陷入局部最优。
在加入并行混沌优化方法后,式(10)的表现形式为
(13)
(14)
式中n为隐含层节点个数;p为优化变量的个数。优化后变量的搜索范围表示为
(15)
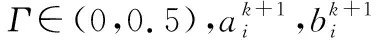
2.2 在线连续学习
与传统CELM算法相比,PCOS-ELM定位算法对隐含层输出权值矩阵β进行矩阵分解,使得新增的在线校准数据能够对初始位置估计模型进行动态调整,从而完成在线学习的功能。
(16)
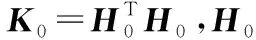

(17)
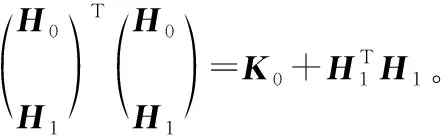
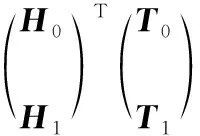
(18)
则β(1)可写为
(19)
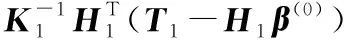
(20)
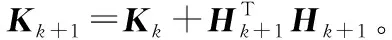
从式(20)可以看出,该算法中当添加新指纹数据时,不需要将原始训练数据重新纳入计算,从而大幅减轻了计算量,同时利用新增的样本信息对训练模型进行修正,提高了对环境的适应性。
基于PCOS-ELM的指纹定位算法具体步骤如下:
1)给定一个指纹训练数据集,设置初始化PCOS-ELM算法的隐含层节点个数L=0,最大迭代次数K=p×M,p为优化变量个数,M为搜索步数。
2)对隐含层节点个数进行增量添加,L=L+1,并通过PCOS算法求取隐含层节点参数最优解。
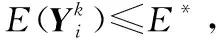
c.根据式(11)、式(12)计算隐含层输出权值和误差。若输出误差EL小于期望误差η,则完成初始化定位模型的构建并转至步骤(3);否则,则转至步骤(2)继续进行隐含层节点增量添加,并对隐含层参数的进行优化搜索。
3)在线阶段将新采集到的指纹数据块添加到初始化定位模型之中,得到最新的隐含层输出矩阵Hk+1。
4)根据式(20),利用新增位置指纹数据对定位模型进行动态调整。
5) 将测试数据输入到调整后的模型中,得出估计的位置坐标。
3 实验与结果分析
本文位置指纹数据的采集点位于江南大学物联网学院5楼,实验的覆盖范围为20 m×15 m的室内环境,AP节点采用TL-WR885N,移动设备采用华为P6手机。指纹数据库中的数据信号强度如表1。
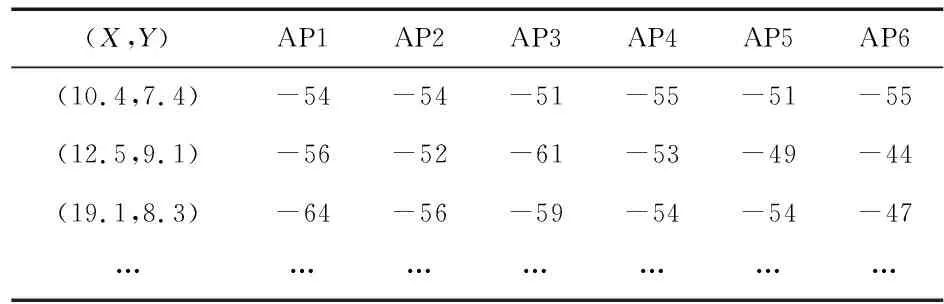
表1 部分指纹数据 dBm
对于PCOS-ELM算法,迭代次数K为影响算法性能重要参数之一。如图1所示由各算法迭代次数与定位误差关系知:ELM和CELM算法的定位误差在初始阶段波动较大,在加入PCOS算法后,实验结果不再随着代次数的增加而大幅振荡。另外,PCOS-ELM算法在迭代50次左右时,定位误差趋于稳定。相比ELM算法和CELM算法,定位误差降低了34 %和23 %。

图1 各算法迭代次数与定位误差关系
图2为各算法迭代次数与训练时间关系,可以看出:ELM算法所需训练时间最长,而PCOS-ELM算法的训练时间与CELM算法类似。当迭代次数为50左右,即PCOS-ELM定位误差收敛时,所需时间为1.8 s,满足实际定位的需要。
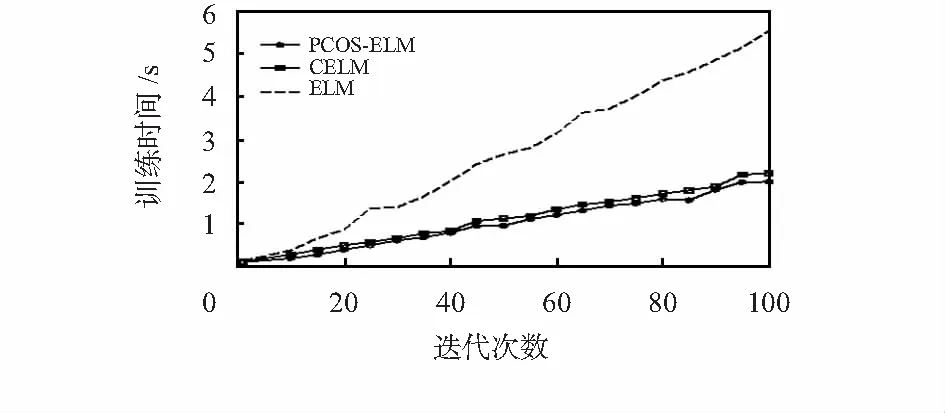
图2 各算法迭代次数与训练时间关系
本实验中算法并行混沌搜索的最大迭代次数K置为50。各算法的误差累积分布概如图3所示,可以看出:定位误差在1.5 m范围内,ELM和CELM算法误差累积分布概率仅为63 %和54 %,PCOS-ELM算法的误差累计分布概率达到81 %,有效提高了定位精度。
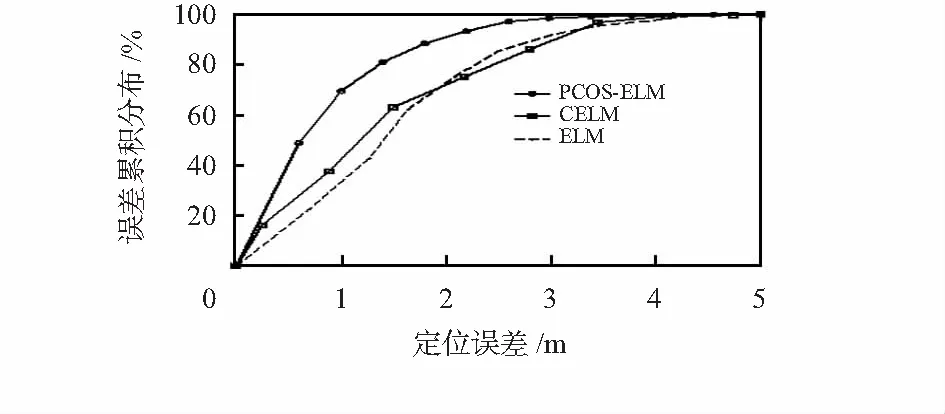
图3 各算法的误差累积分布概率
为了验证PCOS-ELM定位算法对环境的适应性能,本文在不同时间段内采集100个在线校准数据,对模型进行在线动态调整。由图4可知ELM随着新的指纹数据的加入,定位精度下降最为迅速,而CELM的精度也有着较大程度的下降。只有本文提出的PCOS-ELM算法,由于添加了在线连续学习功能,定位误差保持在1.75 m左右,相比初始阶段最终的定位误差仅下降了4.52 %。因此,与传统的批量学习算法相比,基于PCOS-ELM的室内指纹定位算法对动态环境的适应能力有着显著提高。
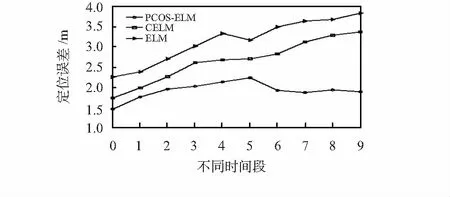
图4 不同时间段内算法定位误差变化
4 结 论
提出了基于PCOS-ELM的室内指纹定位算法,在传统CELM算法基础上,通过并行混沌优化和在线连续学习的方法,解决了传统指纹定位算法定位精度低以及对环境动态调整能力弱的问题。从实验仿真结果可以看出,算法的定位精度及对不同时间段内环境的适应性明显提高。
