基于无先验探测概率的改进PHD多目标跟踪算法*

2018-08-03余哲翔陈思汉

传感器与微系统 2018年8期

余哲翔，陈思汉，白傑

(同济大学汽车学院，上海 201804)

0 引言

多目标跟踪是目前多源传感器数据融合领域的一个重点研究问题。在多目标跟踪过程中,存在目标数目未知、探测概率未知等不利因素。传统的多目标跟踪算法通常基于数据关联算法[1～3]，将多目标跟踪问题转化成多个单目标的跟踪问题。许多学者基于随机有限集(random finite set,RFS) 理论，提出了概率假设密度(probability hypothesis density,PHD)滤波器[4～7]以解决多目标跟踪问题。该算法将复杂的多目标状态空间运算转换为单目标状态空间内的运算，有效避免了多目标跟踪中复杂的数据关联组合问题。因为PHD 滤波器的递推公式中含有多个积分计算，所以不存在非线性非高斯条件下的解析形式。为此文献[8]提出了序贯蒙特—卡罗概率假设密度(sequential Monte Carlo PHD,SMC-PHD) 滤波器,文献[9]提出了高斯混合概率假设密度(Gaussian mixture PHD,GM-PHD) 滤波器。在线性高斯假设条件下，GM-PHD通过采用混合高斯形式近似完全后验概率密度来提高系统执行效率，可以避免SMC-PHD大量撒点带来的较大计算量[10]。传统的PHD滤波器基于固定的探测模型，通常假定探测概率已知。然而在实际情况下，受传感器不同应用环境的影响，探测概率通常未知。Mahler R P S等人[11]提出了一种基于Beta函数的GM-PHD(Beta GM-PHD)算法，使用Beta函数来描述检测概率的分布，在滤波过程中自适应估计未知检测概率。文献[12]提出了一种基于时变卡尔曼滤波(time-varying Kalman filtering,TV-KF)的PHD，算法将目标与量测值进行预关联，通过关联结果来确定目标的检测概率。但此算法使用全部量测数据集对不同类型的目标(包括存活目标、新生目标等)进行更新，增加了无关量测的影响，导致目标估计性能下降。

在上述研究的基础上，本文提出改进的TV-GM-PHD(improved TV-GM-PHD，ITV-GM-PHD)。仿真实验结果表明，本文方法有效可行，优于传统的GM-PHD。

1 GM-PHD 多目标跟踪算法不足

传统的GM-PHD在更新步骤中使用了未知的检测概率pD,k，而对检测概率估计偏差将会使GM-PHD滤波器的性能下降[13]；传统GM-PHD使用所有的量测数据对高斯项进行更新，使得整个观测空间中的杂波都参与更新计算，导致对目标状态估计性能的下降。

2 ITV-GM-PHD滤波算法

2.1 椭球门限

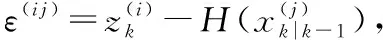
(1)

用Tg表示门限值，则椭球门限的判别式可以表示为

(ε(ij))T(s(j))-1ε(ij)≤Tg

(2)

2.2 多目标ITV-GMP-HD跟踪算法

假设目标在k-1时刻的后验强度函数为

(3)

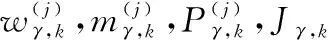
1)预测步：不考虑衍生目标，将对目标后验强度函数的预测分为存活目标vs,k|k-1(x)和新生目标γk-1(x)两部分

(4)

2)更新步：

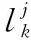
(5)

不同于标准的GM-PHD,式(4)缺少了在目标未被检测时的后验强度函数。这是因为通过预关联步骤确认了该高斯分量已被检测,从而避免使用未知的检测概率PD,k。

b.匹配新生目标的更新。在新生高斯分量集合中找出存在量测值的新生高斯分量xγd，根据xγd，在剩余量测集合zs_out中划分出与新生目标匹配的量测值集合zγ，剩下的未与任何高斯分量匹配的量测值被认为无效量测值zout。利用zγ对匹配新生目标xγd进行更新

(6)

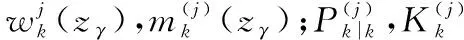
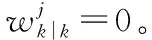
(7)

由于使用椭圆门限对量测集合进行了划分，因此需要重新计算式(5)中存活目标量测的杂波强度函数κk(zs)和式(6)中新生目标量测的杂波强度函数κk(zγ)

(8)

式中Vgk(zs)和Vgk(zγ)分别为存活目标和新生目标的观测空间。

对更新步骤得到的高斯分量进行合并，作为k时刻总的目标强度函数为

vk|k(x)=vk|k(xsd)+vk|k(xγd)+vk|k(xnod)

(9)

对强度函数vk|k(x)中的权重低的高斯分量进行裁剪，相近的高斯分量进行合并，具体过程详见文献[9]，最终获得目标的状态估计。

3 仿真实验与分析

通过仿真二维空间中多个不规则运动目标来测试验证本文算法的有效性，并与传统GM-PHD算法进行比较，即在低杂波强度下比较2种算法的性能，通过多杂波强度实验以观察2种算法性能的鲁棒性。实验中,假设目标在[-1 000,1 000]m×[-1 000,1 000]m的监视区域范围内运动，目标状态及起始和结束时间参数设定如表1所示。

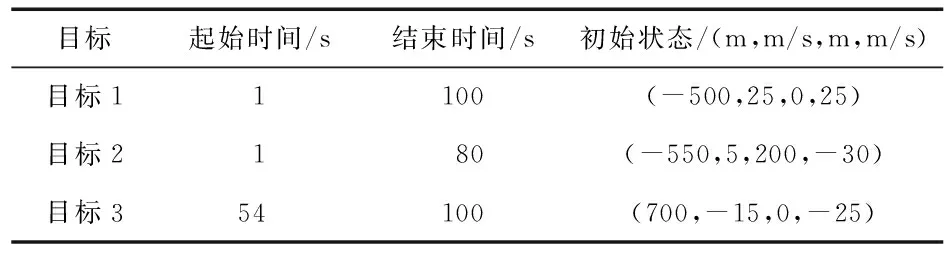
表1 目标运动状态

新生目标的强度函数为

(10)

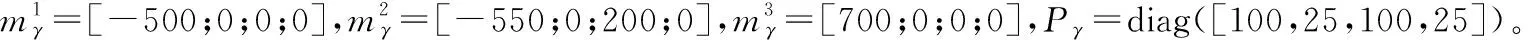
(11)

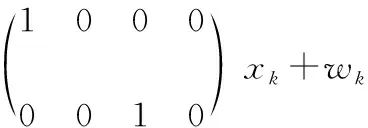
(12)

设杂波均匀分布在整个观测空间,杂波强度λk=10。目标的运动轨迹和量测结果如图1所示。

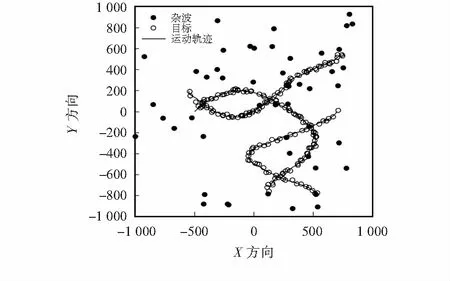
图1 目标运动轨迹和量测结果

实验中，目标存活概率ps=0.99，高斯分量的修剪阈值T=10-5,合并门限U=4，高斯分量的最大个数Jmax=100。

真实检测概率pD=0.9，而在传统GM-PHD中，假设对检测概率存在估计偏差，预设的检测概率pD_s=0.95。针对以上仿真数据,传统GM-PHD滤波算法和本文提出方法的跟踪结果如图2所示。

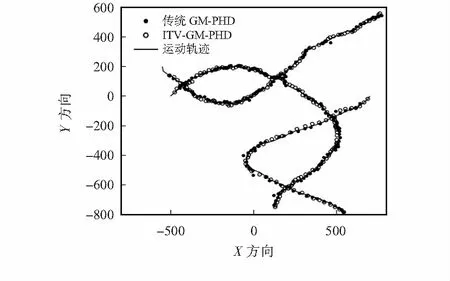
图2 目标运动轨迹和估计结果

可知，大体上,2种方法可以有效过滤杂波虚假目标,实现对设定目标的有效跟踪,但传统GM-PHD滤波器存在漏检现象，本文算法的跟踪效果相对更加稳定连续。

本文利用目标数目估计及最优子模型指派(optimal sub-pattern assignment,OSPA)距离作为评价指标,比较2种算法的性能。OSPA距离的计算公式为

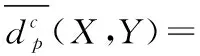
cp(n-m)))1/p

(13)

式中X,Y为两个随机的集合；dc(xi,yπ(i))为两集合各元素的距离；n和m分别为两个集合的维数；p为距离的阶数，实验中p=2，c=100。

图3、图4、表2以及表3为20次实验结果的平均值。图3和表2为目标数估计结果，由图3可以看出，传统的GM-PHD的目标数估计结果比真实值更小，且偏差较大；而本文算法的估计结果在真实值附近波动，偏差更小，更接近真实值。根据表2，传统GM-PHD算法的目标数估计平均正确率为67.6 %，而本文算法为89.2 %，高出21.7 %。

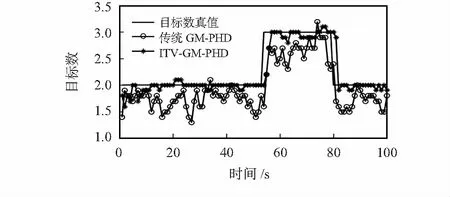
图3 目标数估计比较结果

图4和表3为OSPA距离结果，由图4可以看出，本文算法的OSPA平均距离明显小于传统GM-PHD算法。根据表3，传统GM-PHD算法的OSPA平均距离为30.133 5 m，而本文算法的OSPA距离为17.617 3 m，下降12.516 2 m。

由于在传统的GM-PHD滤波器中，预设的检测概率p(D_s)大于真实的检测概率pD，滤波器的性能有所下降[13]。在多数时间内，估计的目标数都小于真实值。而本文算法通过对目标和量测值进行预关联，可以确定每个目标的检测概率，因此对目标数的估计更为准确。且OSPA距离由目标状态估计精度和目标数估计正确率共同决定，由于本文算法对目标数的估计更为准确，且只采用相关性较高的量测对高斯项进行更新，因此降低了无关量测的影响，从而对目标状态的估计精度更高，使得OSPA距离更小。

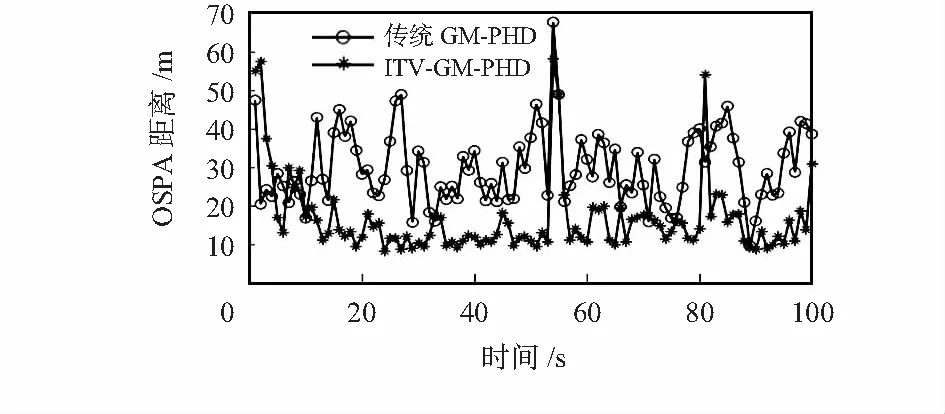
图4 OSPA距离比较结果

设置多组实验验证2种算法在不同杂波强度环境下的鲁棒性，实验中,杂波强度λk从10逐渐增加到50，实验结果如表2、表3所示。

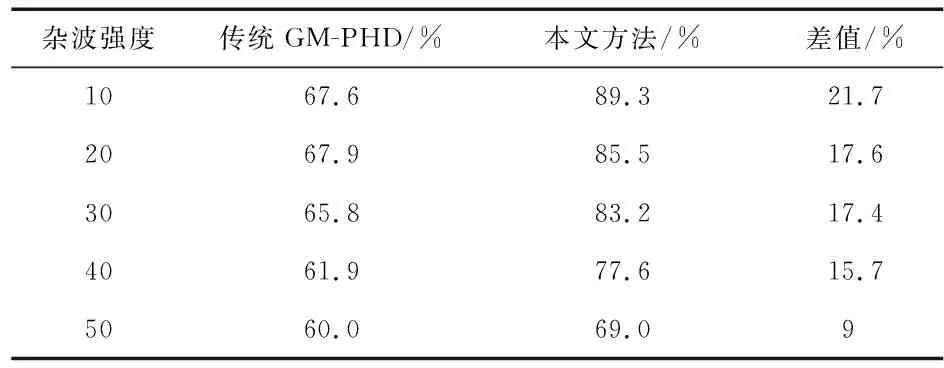
表2 目标数估计平均正确率

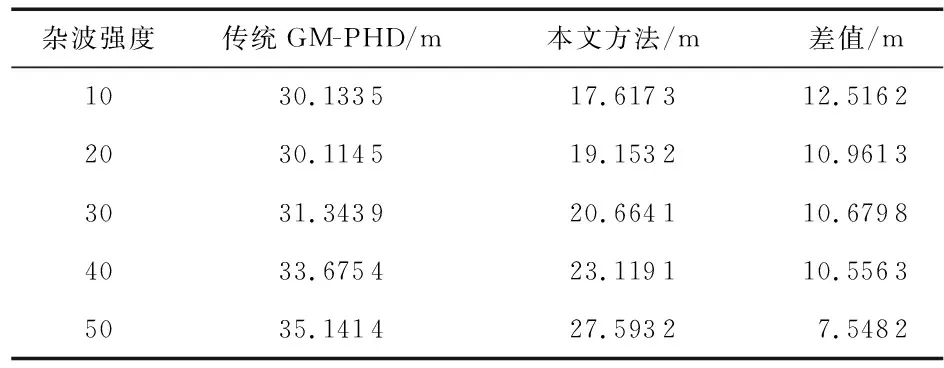
表3 平均OSPA距离

可知,随着杂波强度增强，2种算法的性能逐渐下降。首先，随着杂波强度增强，估计的目标数逐渐大于真实值，之后与真实值的偏差逐渐增大，因此,目标数估计正确率逐渐下降。其次，因为杂波强度增加使得杂波量测对目标估计产生的影响增加，继而目标状态估计精度下降，最终导致OSPA距离不断增大。

在杂波强度处于10～40阶段时，本文算法目标数估计正确率较传统GM-PHD高出15 %以上，平均OSPA距离较传统GM-PHD低10 m左右。在杂波强度为50时，本文算法与传统GM-PHD算法的性能差距有所减小，但依然优于传统GM-PHD。在实际应用场景下，可以通过对传感器检测到的目标设置过滤条件，控制杂波数目在一个相对较低的水平，以最大限度的发挥本文算法的优势。