基于粒子群优化的RSSI等弧三边定位算法*

刘旭明， 王 伟， 景 强， 郭志慧

(中北大学 信息与通信工程学院，山西 太原 030051)

0 引 言

室内定位对精度有更严格的要求，相比于室外定位，室内定位的可靠性、连续性和稳定性较差[1，2]，室外定位系统在室内定位中存在精度不够、信号不稳定等问题，不能实现从室内到室外定位的无缝对接[3]。室内定位技术基于无线传感器网络(wireless sensor networks,WSNs)的节点定位方法按测距与非测距主要有2类：基于测距的定位算法和基于非测距的定位算法。前者通过接收信号强度指示(received signal strength indication,RSSI)、到达时间(time of arrival,TOA)、到达时间差(time difference of arrival,TDOA)或到达角(angle of arrival,AOA)[4]等测度方式获得节点间的相对位置关系(如距离、角度)，然后根据三边测量[5]、三角测量[6]、最大似然估计法或粒子群算法[7]等定位算法计算盲节点位置。

本文首先基于对数损耗模型的距离与RSSI关系进行分析，得出不同距离范围与RSSI的相对应关系，提出等弧三边形的定位算法。在相同的实验环境下，分别采用方形布局[8]、等边三角形布局[9]、改进的三角形布局[10]与本文定位效果进行对比，验证提出算法的优越性。

1 RSSI与距离的关系

在实际中，由于多径效应等因素的影响通常采用对数损耗传播模型评估距离和RSSI的关系

(1)

式中d0为近地参考距离；Pr(d0)为近地参考距离的路径损耗值;d为实际距离；Pr(d)为实际距离d的精确路径损耗；n为路径损耗因子，随环境的改变而变化；X为随机噪声,忽略不计。通常d0为1 m，Pr(d0)通过测量可得，记为A;i为不同位置的标记值。则不同位置处距离di与RSSIi的关系为

RSSIi=A-10nlgdi,i=1,2,3,…

(2)

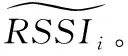
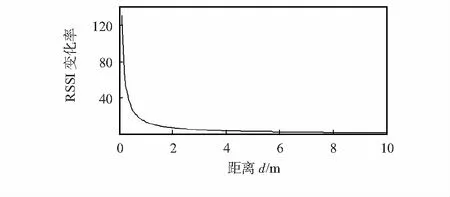
图2 RSSI变化率与距离的关系

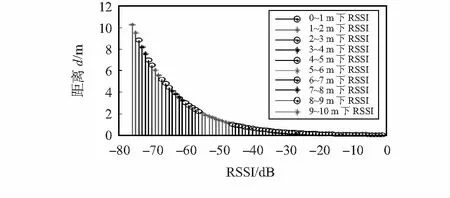
图3 RSSI与距离关系

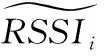
2 等弧三边形定位算法

2.1 等弧三边模型

图4 等弧三边形节点布署示意

图4中在等弧三边形ABC所围成的区域中，有部分区域也在等弧三边形ACD所围成的区域中。位于重叠区域的待测点，能在2种组合中选择最优的一组进行定位，防止由于干扰等原因出现异常，从而这种选择性对定位精度的提升起到辅助作用。

2.2 等弧三边形布局控制RSSI异常值

与传统三角形定位布局不同，本文以所选取的通信距离r为界，通过对数衰减模型对基站选出的3个最优RSSI值进行计算。如果得到的距离大于通信距离r，判定当前值为异常值，基站重新选出3个最优RSSI值进行计算，最大采集次数为3次。如果采集3次后仍有超越距离r的值，则定位系统将当前异常值重新赋值为r，本文r为4 m。

2.3 等弧三边形定位算法

结合标准粒子群算法和等弧三边形布局，本文定位算法步骤如下：

1)初始化信标节点网络模型。

2)未知节点周期性发送自身信息。

3)各信标节点在收到信息后，记录同一个未知节点的RSSI测量值，并将其值记录到对应的RSSI数组中。

4)各信标节点运用卡尔曼滤波处理RSSI值。

5)各节点将步骤(4)中得到的RSSI值传送到基站，由基站将各节点的RSSI值进行排序，取其最大的3个值，并转换为距离，分别为d1，d2，d3。

6)判断d1，d2，d3是否大于r:是，重新取值，累计3次仍大于r,则按r(r=4 m)计；否则，按原值计算。(方形布局模型没有此步骤)

7)利用标准粒子群优化定位算法，迭代10轮，每轮搜索100次，计算待测点位置(x，y)。

3 实验分析

3.1 实验布局

在实验室一个8 m×8 m的区域内，分别按照方形布局、传统三角形布局、改进三角形布局和等弧三边形布局部署信标节点，如图5中所示。倒三角代表信标节点，“×”代表待测节点。10个待测节点坐标分别为(1,1),(2,2),(3,3),(4,4),(5,5),(4,7),(1,4),(7,4),(2,7),(6,7)。选取最佳通信距离为4 m。

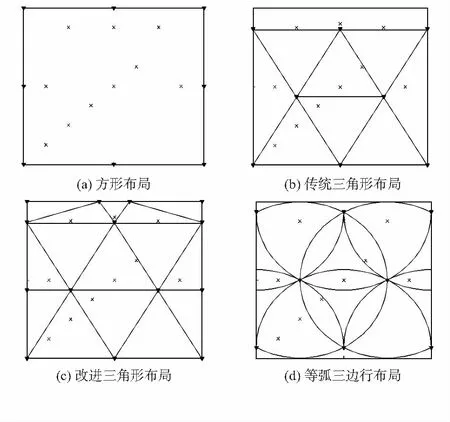
图5 4种布局的节点分布

3.2 结果分析

通过对比4种布局类型，易知图5(a)中方形布局未涉及任何细化的区域模型；图5(b)中传统三角形布局面积覆盖率为65 %，即42 m2；图5(c)中改进三角形布局虽然能够全覆盖，但增加了6个节点；图5(d)中等弧三边形布局面积覆盖率为88 %，即56 m2，相比图5(b)和图5(c)中布局模型，等弧三边形布局的单位节点面积覆盖率更高。

对4种定位布局的数据处理后，得到4种定位布局的误差对比，如表1所示，可知，等弧三边形布局较方形布局、传统三角形布局和改进三角形布局的平均定位精度，分别提高了81 %,54 %和48 %。

表1 4种布局最大、最小和平均误差对比 m

得出如下结论：

1)4种定位布局中，等弧三边形具有最好的定位精度，传统三角形和改进三角形布局次之，方形布局最差。

2)改进三角形布局和传统三角形布局在前5个点的测试中，定位精度差别不大；在后5个点中，改进三角形布局较传统三角形布局有所提高，其主要原因是多增加了几个节点。比较2种布局的10个待测点，改进三角形布局较传统三角形布局，平均定位精度提高了12 %。

4 结束语

通过对RSSI与距离的关系分析，得到距离越远RSSI越不稳定，基于对数衰落模型的距离容错率越来越低，测距误差越来越大。为了利用测距精度较高的信号，提出了等弧三边形定位算法。该算法相对传统方形布局、传统三角形布局和改进三角形布局有更优的定位效果。本文算法不仅能有效提高定位精度，而且能合理控制节点成本,适合大范围推广。